一种EMD风噪抑制下的Mel谱多维特征空间的声音识别方法
- 国知局
- 2024-06-21 11:39:13
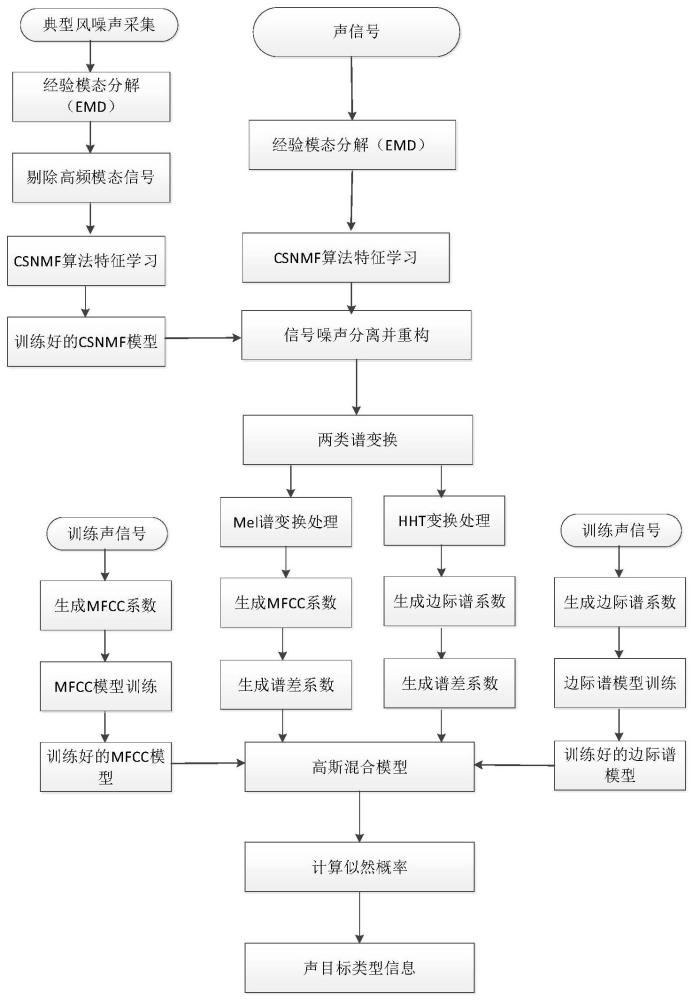
本发明属于信号处理领域,具体涉及一种emd风噪抑制下的mel谱多维特征空间的声音识别方法。
背景技术:
1、常见的声目标只要分为两类:连续声和脉冲声。脉冲声是指短时间内突变的、不具有连续性的声音信号。连续声是指相对于脉冲声,具有时间上连续的声音。常见的脉冲声信号如枪声、炮声、雷电声、关门声等声信号,连续声如直升机声、无人机声、语音等。传统的声识别方法有小波变换、自相关、过零率分析、频谱分析、线性预测分析等理论的声信号识别方法。一般情况下,传统声识别方法可以取得不错的识别率,能有效区分出目标信号和干扰信号;但是,当噪声信号与目标信号具有相同的频率范围,频谱重叠时,传统方法就很难将噪声信号从目标信号中分离出来,造成较高的虚警率,识别结果不理想,因此,需要切实有效的降噪方法以降低噪声对目标信号的影响。
2、另一方面,近年来,新型声音识别方法不断被提出来,应用较为广泛的方法是:通过提取声音信号的mel谱系数特征,运用隐马尔可夫模型(hmm),识别出目标脉冲声信号。这种方法已经在语音识别及模式识别中得到了广泛的应用。但这种方法也有局限性,其不能很好的表达非线性非平稳声信号的局部时域特征,不能进一步精确的识别出时频特征的细节。
3、下面介绍现有的、传统的声目标识别方法,图1为hmm算法流程图。
4、首先,根据mel谱理论,生成mfcc系数及其一阶谱差系数;计算各系数的hmm概率密度函数,生成训练好的hmm模型。其次,将声信号进行模型匹配,计算匹配的最大似然概率,找到最大概率所对应的声信号的种类,此种类就是待识别声信号的类型。识别完毕。
5、以下两部分是基于美尔谱变换的hmm算法的实现原理和步骤。
6、(1)基于美尔谱变换的特征提取
7、mel频率倒谱系数简称为mfcc(mel-frequency cepstral coefficents),其分析着眼于人耳的听觉特性,因为,人耳所听到的声音的高低与声音的频率并不成线性正比关系,而用mel频率尺度则更符合人耳的听觉特性。所谓mel频率尺度,它的值大体上对应于实际频率的对数分布关系。mel频率与实际频率的具体关系可用下式表示:
8、mel(f)=2595lg(1+f/700)
9、这里,实际频率的单位是hz。临界频率带宽随频率的变化而变化,并与mel频率增长一致,在1000hz以下,大致呈线性分布,带宽为100hz左右;在1000hz以上,呈对数增长。类似于临界频带的划分,可以将语音频率划分成一系列三角形的滤波器序列,即mel滤波器组,如图2所示。
10、mel频率系数在声音识别中具有重要意义,其在语音、枪声、炮声、发动机声、直升机声、各类故障声等方面均有广泛的应用,是识别声音信号的重要特征。
11、(2)mfcc系数的计算
12、mfcc特征参数提取原理框图如图3所示:
13、预处理
14、预处理包括预加重、分帧、加窗函数。预加重是为了补偿高频分量的损失,提升高频分量。加窗一般加汉明窗函数。
15、快速傅里叶变换
16、对每帧信号进行fft变换,从时域数据变为频域数据:
17、x(i,k)=fft[xi(m)] (1.1)
18、计算谱线能量
19、对每一帧fft后的数据,计算谱线的能量
20、e(i,k)=[xi(k)]2 (1.2)
21、计算通过美尔滤波器的能量
22、在频域中,把每帧的能量谱e(i,k)(代表第i帧,第k条谱线)与美尔滤波器的频域响应hm(k)相乘并相加:
23、
24、计算dct倒谱系数
25、序列x(n)的fft倒谱为:
26、
27、式中ft和ft-1表示傅里叶变换和傅里叶逆变换。序列x(n)的dct倒谱为:
28、
29、式中,参数n是序列x(n)的长度;c(k)是正交因子,可表示为
30、
31、把美尔滤波器能量取对数后,计算dct得:
32、
33、δmfcc(i,n)=mfcc(i+1,n)-mfcc(i-1,n) (1.8)
34、式中,s(i,m)是美尔滤波器的能量;m指第m个美尔滤波器(共有m个);i指第i帧数据;n是dct后的谱线;δmfcc(i,n)为一阶差分系数。
35、因此,通过以上公式,生成mfcc系数和差谱系数,该系数作为声目标中美尔谱的一种特征系数,在声目标模型中,作为识别未知声目标的一种判断依据。
36、(3)隐马尔科夫模型原理
37、隐马尔科夫模型(hidden markov models,hmm)作为语音信号的一种统计模型,已经在语音处理各个领域得到广泛的应用。隐马尔科夫模型既解决了用短时模型描述平稳段的信号,又解决了每个短时平稳段是如何转变到下一个短时平稳段的,用概率或统计范畴的理论成功解决了怎样辨识具有不同参数的短时平稳的信号段、怎样跟踪他们之间的转化等问题。
38、hmm是由两个随机过程组成的:一个是状态转移序列,它对应着一个单纯的markov过程;另一个是每次转移时,输出的符号组成的符号序列。其中,第一个随机过程不可观测,第二个随机过程能通过输出观察序列观测。
39、设状态转移序列为s=s1,s2,…st,输出的符号为o=o1,o2,…ot,假设在单纯markov过程中,相邻符号互不相关,即si-1和si之间转移时的输出观察值oi跟其它转移之间无关,则有下式成立:
40、
41、
42、对于隐markov模型,把所有可能的状态转移序列都考虑进去,则有
43、
44、此式就是计算输出符号序列输出概率所用的公式。
45、通过隐马尔科夫原理,计算出未知声目标特征系数的输出概率,将最大输出概率的声目标种类,作为未知声目标的识别结果。目标识别完毕。
46、现有技术的缺点:
47、传统方法缺乏有效的风噪声滤波能力,不能对典型噪声预处理。风噪声在频域内,跟声目标信号有重叠的频带,会严重影响声目标信号的识别率。
48、传统方法是通过提取声音信号的mel谱系数特征,运用隐马尔可夫模型(hmm),识别出目标脉冲声信号。虽然这种方法已经在语音识别及模式识别中得到了广泛的应用,但其也有局限性。传统方法在应对非平稳信号时,识别率偏低。mel谱系数特征不能很好的表达非线性非平稳声信号的局部时域特征,不能进一步精确的识别出时频特征的细节。
49、隐马尔可夫模型(hmm)的概率识别方法,在数据训练、概率计算等环节,计算复杂度较高;在模型中,输入不同的参数,会导致算法的识别精度有波动。因此,传统方法的目标识别精度有待提高。
技术实现思路
1、为精确识别声信号,提高声目标识别率,本发明提出了一种基于emd风噪抑制下的mel谱多维特征空间的声音识别技术。本发明采用经验模态分解(emd)方法,结合非负矩阵分解方法,实现对目标声信号的风噪声抑制;然后,建立声目标的高斯混合模型(gmm),提取声目标的希尔伯特-黄变换(hht)的边际谱系数、mel谱系数以及各谱系数的一阶差分谱等特征参数,将这些特征参数作为声目标的识别参数,更进一步,根据高斯混合模型准则,训练出多维特征空间的特征向量;将未知声目标与已建立的多维特征向量做对比,得到未知声目标的最大输出概率类型,从而识别出声目标类型。
2、本发明一种emd风噪抑制下的mel谱多维特征空间的声音识别方法包括如下步骤:
3、步骤一、对声信号进行经验模态分解,使用非负矩阵分解方法csnmf进行信号的特征学习;同时,对经典风噪声进行经验模态分解,剔除高频模态信息后,使用非负矩阵分解方法csnmf进行信号的特征学习;然后,对声信号进行信噪分离,并重构降噪后的声信号;
4、步骤二、训练标准声信号,根据mel谱理论,生成mfcc系数及其一阶谱差系数;然后,根据希尔伯特-黄理论,生成边际谱系数及其一阶谱差系数;将两类系数合成一体,并计算各系数的高斯概率密度函数,生成训练好的高斯混合模型;将未知声信号进行模型匹配,未知信号经过信号预处理后,进行两类谱变换,分别生成mfcc系数、边际谱系数及相应的一阶差分谱系数;并计算各系数的高斯概率密度函数,生成待识别脉冲的高斯混合模型;
5、步骤三、将训练好的模型和待识别模型相匹配,计算匹配的最大似然概率,找到最大似然概率所对应的脉冲信号的种类,该种类是待识别脉冲信号的脉冲类型,识别完毕。
6、进一步地,步骤一包括:
7、a.建立卷积模型,
8、已知非负矩阵x,寻找一种分解方法,使其等于两个非负矩阵d和c的乘积,采用卷积模型,即:
9、
10、式中x,λ∈r≥0,m×n,d∈r≥0,m×r和c∈r≥0,r×n,矩阵d为基矩阵,其包含的列向量为基向量,矩阵x中的列向量即是由矩阵d里面的基向量线性组合构成;矩阵c为编码矩阵,包含由基向量构建矩阵x的组合方式,r小于m及n,用少量的基向量表征大量的数据向量,
11、在矩阵分解中,目标函数通过两矩阵的差值来构建,构建方法有最小平方准则(ls)散度准则:
12、
13、其迭代公式为:
14、
15、
16、对目标函数收敛性的判断通过计算目标函数的相对变换率来完成,如果目标函数相对变化率小于阈值ε,则认为目标函数收敛;
17、b.建立信号模型,
18、信号由声信号和加性噪声组成:
19、x(t)=s(t)+w(t),
20、对带噪信号进行短时傅立叶变换stft,并将其分成纯净目标信号和风噪声两部分:
21、
22、通过他们的乘积,还原出纯净目标信号:
23、
24、进一步地,步骤二包括:
25、c、经验模态分解:
26、对任意的时间序列x(t),按如下定义得到它的希尔伯特变换为
27、
28、通过上式,定义解析信号z(t):
29、z(t)=x(t)+i·y(t)=a(t)·exp(i·θ(t)),
30、其中,
31、瞬时频率计算公式为:
32、
33、用经验模态分解的方法,分解出瞬时频率的实际物理意义的单分量imf,任何复杂信号s(t)都能表示成n个有实际物理意义的单分量imfk(t),即
34、
35、其中,imfk(t)为有实际物理意义的单分量,k=1,2,3,…n;rn(t)为残余分量,上式是信号的结果,单分量imfk(t)不要求满足线性要求;任何复杂信号均被分解成n个单分量和一个残余分量的组合,
36、d、emd筛选:
37、首先,分别使用信号的局部极大值和局部极小值形成的包络来执行筛选过程,确定所有局部极值点后,上包络由极大值的三次样条曲线连接形成,同样,下包络由极小值的三次样条曲线连接形成,这样信号所有数据点位于上下包络围成区域内部,原始信号s(t)上下包络的均值,记为m1(t),则s(t)与m1(t)之差为第一个分量,记为h1(t):
38、s1(t)-m1(t)=h1(t),
39、在第二次筛选中,把h1(t)视为原始信号,运用同样的方法,可得到:
40、h1(t)-m1,1(t)=h1,1(t),
41、然后同样地重复筛选过程k次,直到h1,k(t)满足imf的条件,为第一个imf分量,这一过程表示如下:
42、
43、记imf1,t(t)=h1,k(t),这样imf1,t(t)就是从原始信号s(t)中筛选出的第一个imf分量,我们将这个层面上的筛选称为内层筛选,内层筛选过程仅仅依靠特征时间尺度最先从信号中分解出最细尺度的局部模态,通过下式将imf1,t(t)与s(t)的其它分量分离开来:
44、s1(t)-imf1(t)=r1(t)
45、r1(t)中包含着s(t)除外imf1,t(t)的其余分量,于是将r1(t)视为新的待分解信号,运用相同的内层筛选过程作用于r1(t),重复以上步骤,可得:
46、
47、因此,emd方法将非线性、非平稳信号的分解成一组imf的分解方法,分解结果为:
48、
49、通过分解之后,舍弃非imf分量,将每个作hilbert变换的结果表示为:
50、
51、其中,
52、
53、
54、h为希尔伯特变换运算符,
55、hilbert谱的定义为:
56、
57、用幅度的平方表示能量密度,将hilbert谱中的幅度取平方,则得到希尔伯特能量谱,定义希尔伯特边际谱h(ω)和瞬时能量密度级ie(t),分别为:
58、
59、δh(ω)=h(ωt+1)-h(ωt-1),
60、其中,t为信号采样时间,信号边际谱h(ω)反映了每个频率点上幅度值的分布,代表了在概率意义上沿整个数据跨度的累积幅度,也揭示了每个频率在整体上的幅度贡献;δh(ω)定义了边际谱的一阶差分系数;
61、e、高斯混合模型gmm的数据训练:
62、一个m阶高斯混合模型的概率密度函数是由m个高斯概率密度函数加权求和得到的,如下:
63、
64、式中,x是一个d维随机向量;bi(xi),i=1,…,m是子分布;ωi是混合权重;每个子分布是d维的联合高斯概率分布,表示为:
65、
66、式中,μi是均值向量,σi是协方差矩阵,混合权重值满足以下条件:
67、
68、完整的混合高斯模型由参数均值向量、协方差矩阵和混合权重组成,表示为:
69、λ={ωi,μi,σi},i=1,…,m,
70、对于给定的时间序列x={xt},t=1,2,…,t利用gmm模型求得的对数似然度定义为:
71、
72、对于一组长度为t的训练矢量序列x={x1,x2,…,xt},gmm的似然度表示为:
73、
74、采用em算法估计参数λ,混合权值的重估公式:
75、
76、均值的重估公式:
77、
78、方差的重估公式:
79、
80、其中,分量i的后验概率为:
81、
82、em参数估计算法步骤如下:
83、输入:观测变量x={xj},j=1,2,…,n,误差ε,迭代次数m,
84、输出:θ={(ωi,μi,σi),i=1,…,q},
85、步骤1)、初始化参数,令m=1;
86、步骤2)、迭代:
87、e步骤:利用统计平均思想,计算观测值xj来自第i个模型的概率:
88、
89、m步骤:利用计算得到的概率估计,计算最大似然得到的模型参数:
90、
91、
92、
93、若m≥m,则跳至步骤3);否则,计算参数迭代误差,若||θm-θm-1||≤ε,则跳至步骤3),否则m=m+1,返回步骤2)中第1步继续迭代;
94、步骤3)、输出最后的即为估计结果,em参数估计算法结束。
95、进一步地,步骤三包括:
96、最大后验概率表示为:
97、
98、
99、由于p(λi)的先验概率未知,假定未知声目标属于训练集中每类的概率相等,这样,识别未知声目标公式就可以表示为:
100、
101、i为识别出的脉冲信号种类。
102、本发明采用经验模态分解(emd)方法,结合非负矩阵分解方法,实现对目标声信号的风噪声抑制;采用基于emd的风噪抑制技术,运用多维特征空间识别技术,能精确识别出声目标特征,提高了目标识别率,降低了虚警率。
本文地址:https://www.jishuxx.com/zhuanli/20240618/22688.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请发送邮件至 YYfuon@163.com 举报,一经查实,本站将立刻删除。