一类基于克罗内克分解的时域多通道语音降噪方法

本发明涉及语音降噪领域，特别是涉及一类基于克罗内克分解的时域多通道语音降噪方法。

背景技术：

1、在日常环境中，存在各种类型的噪声，麦克风采集到的语音信号必然会被各种环境噪声所污染，噪声使得语音信号的质量和可懂度降低，并且会导致听者的听力疲劳。所以语音降噪技术显得尤为重要。语音降噪技术致力于抑制噪声的影响，目的是从带噪语音信号中恢复出“纯净”的语音信号，进而提高语音的质量和可懂度，在语音通信中起着重要作用。

2、根据语音降噪算法是否利用空间信息，可分为单通道降噪算法和多通道降噪算法。根据语音降噪算法执行域的不同，降噪算法又可分为时域算法和变换域算法(如小波域及频域等)。目前，频域语音降噪方法的应用范围较广。原因在于频域降噪方法的复杂度低，可实现实时降噪。但其缺点是容易产生音乐噪声(musical noise)。经研究，相比日常生活中的噪声，人们更加难以忍耐音乐噪声。因此，降低频域降噪算法产生的音乐噪声一直是研究人员的研究热点。而时域语音降噪方法的优势则恰恰是不会产生音乐噪声。但限制时域语音降噪方法实际部署的最大瓶颈是其复杂度较高。原因是在时域语音降噪算法中，其滤波器通常较长，导致复杂度过高。尤其是对于多通道语音降噪算法，很难部署在实际系统中对带噪语音信号进行实时降噪处理。另外，应用较长的滤波器还会带来以下两个问题：第一，信号相关矩阵的估计误差会随着滤波器长度的增加而增加，最终会导致算法降噪性能的下降；第二，需要更多的观测样本来估计信号的相关矩阵，用以计算滤波器的系数，导致算法对信号统计特性变化的跟踪能力下降。

3、为解决上述问题，本发明中提出一类基于克罗内克分解的时域多通道迭代降噪滤波器的设计方法。

技术实现思路

1、本发明的目的是提供一类基于克罗内克分解的时域多通道语音降噪方法，以解决上述现有技术存在的问题。

2、为实现上述目的，本发明提供了一类基于克罗内克分解的时域多通道语音降噪方法，包括：

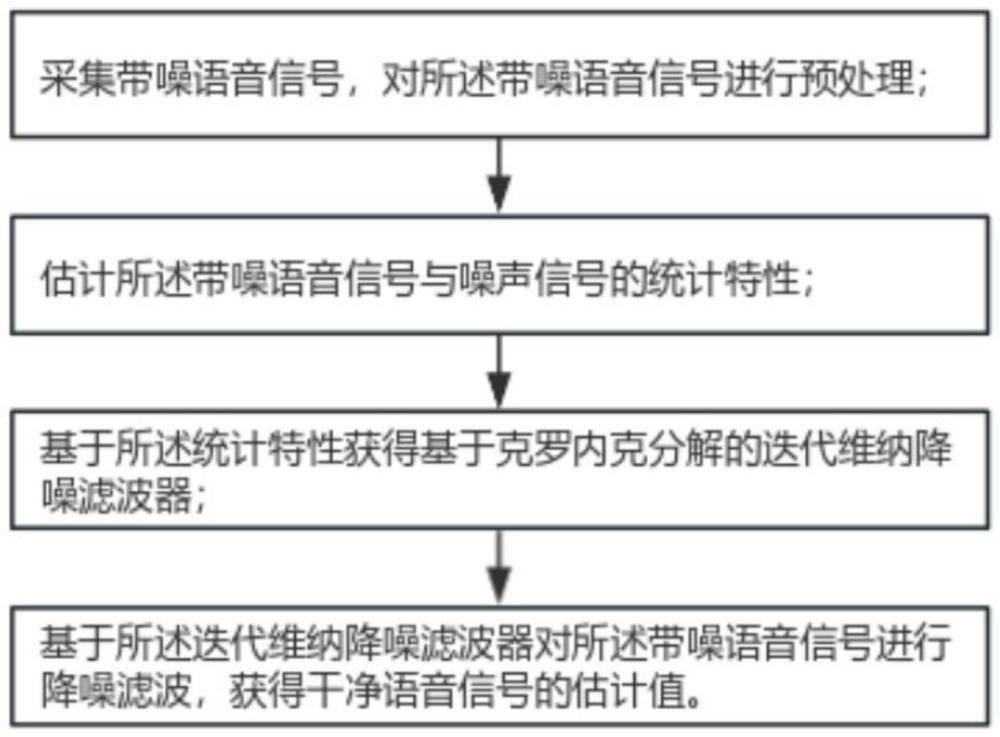
3、采集带噪语音信号，对所述带噪语音信号进行预处理；

4、估计所述带噪语音信号与噪声信号的统计特性；

5、基于所述统计特性获得基于克罗内克分解的迭代维纳降噪滤波器；

6、基于所述迭代维纳降噪滤波器对所述带噪语音信号进行降噪滤波，获得干净语音信号的估计值。

7、可选的，采集带噪语音信号，对所述带噪语音信号进行预处理的过程包括：

8、在语音降噪中，时域信号模型为：

9、ym(t)＝xm(t)+vm(t)  (1)

10、这里，t表示离散时间点，下标(·)m表示第m个麦克风接收到的信号(本发明中设麦克风阵列共有m个麦克风)，xm(t)和vm(t)分别表示第m个麦克风接收到的干净语音信号和加性噪声信号，ym(t)表示第m个麦克风接收到的带噪语音信号，xm(t)和vm(t)互不相关；选取麦克风阵列中的第1个麦克风作为参考麦克风，即x1(t)作为期望信号；

11、通过将l个连续的样本点组合在一起，将第m个麦克风接收到的信号写成长度为l的向量：

12、

13、其中，xm(t)和vm(t)的定义和ym(t)相似，即：

14、xm(t)＝[xm(t) xm(t-1) … xm(t-l+1)]t

15、vm(t)＝[vm(t) vm(t-1) … vm(t-l+1)]t

16、xm(t)和vm(t)分别表示第m个通道的期望信号向量和第m个通道的噪声信号向量，ym(t)表示第m个通道的带噪信号向量，上标(·)t表示转置；

17、将m个长度为l的带噪信号向量ym(t)(m＝1,2,...,m)拼接在一起，写成：

18、

19、其中，x(t)和v(t)的定义方式与y(t)相同，即

20、

21、

22、y(t)、x(t)和v(t)分别表示整体带噪信号向量、整体干净语音信号向量以及整体噪声信号向量。

23、可选的，估计所述带噪语音信号与噪声信号的统计特性的过程包括：

24、通过现有噪声估计算法估计所述整体噪声信号向量v(t)的相关矩阵rv(t)，通过递归算法估计整体带噪信号向量y(t)的相关矩阵ry(t)：ry(t)＝αry(t-1)+(1-α)y(t)yt(t)，其中α为遗忘因子(0＜α＜1)；通过rx(t)＝ry(t)-rv(t)估计整体干净语音信号向量x(t)的相关矩阵rx(t)，基于语音信号相关矩阵rx(t)确定向量ρ(t)，获得统计特性。

25、可选的，基于语音信号相关矩阵rx(t)确定向量ρ(t)的过程包括：

26、提取所述语音信号相关矩阵rx(t)第一行第一列的元素与第一列的元素，第一列的元素除以第一行第一列的元素获得向量ρ(t)。

27、可选的，基于所述统计特性获得基于克罗内克分解的迭代维纳降噪滤波器的过程包括：

28、构建与所述整体带噪信号向量具有同等长度的线性滤波器的对应矩阵，对所述矩阵进行奇异值分解并进行近似表示，基于奇异值分解结果的近似表示，获得同等长度的线性滤波器的近似表示；

29、基于线性滤波器的近似表示对期望信号估计值的表达式进行改进，采用滤波后的语音信号与滤波后的残留噪声表示期望信号估计值；

30、定义期望信号估计值的均方误差，基于线性滤波器的近似表示对所述均方误差进行变形，基于变形后的均方误差表达式获得基于克罗内克分解的迭代维纳滤波器。

31、可选的，构建与所述整体带噪信号向量具有同等长度的线性滤波器的对应矩阵，对所述矩阵进行奇异值分解并进行近似表示，基于奇异值分解结果的近似表示，获得同等长度的线性滤波器的近似表示的过程包括：

32、为了达到降噪的目的，需要将长为ml的整体带噪信号向量y(t)通过一个线性滤波器h(t)，即

33、

34、其中，z(t)为期望信号x1(t)的估计值，hm(t)(m＝1,2,…,m)为第m个通道的线性滤波器，长度为l，h(t)为长度为ml的线性滤波器；

35、为导出基于克罗内克分解的时域多通道降噪方案，将hm(t)(m＝1,2,...,m)写为矩阵形式，即

36、h(t)＝[h1(t) h2(t) … hm(t)]  (5)

37、应用奇异值分解，矩阵h(t)可分解为如下形式：

38、

39、其中，h1(t)＝[h1,1(t) h1,2(t) … h1,l(t)]和h2(t)＝[h2,1(t) h2,2(t) … h2,m(t)]分别为由矩阵h(t)的左奇异向量h1,l(t)(l＝1,2,...,l)和右奇异向量h2,m(t)(m＝1,2,...,m)构成的正交矩阵，维数分别为l×l和m×m，σ(t)是一个维数为l×m的矩形对角矩阵，其对角线元素为矩阵h(t)的奇异值，为非负实数；将奇异值从大到小排列，即σ1(t)≥σ2(t)≥…≥σm(t)≥0；

40、用前p(p≤min(m,l))个最大奇异值对应的奇异向量来逼近矩阵h(t)，即

41、

42、其中，h1,p(t)为矩阵h(t)的奇异值σp(t)(σp(t)为矩阵h(t)的从大到小排列的第p个奇异值)对应的左奇异向量(p＝1,2,...,p)，h2,p(t)为矩阵h(t)的奇异值σp(t)对应的右奇异向量(p＝1,2,...,p)，

43、基于式(7)，滤波器h(t)可以近似表示为

44、

45、其中，h(t)＝vec[h(t)]，符号vec[·]表示矩阵的向量化操作，符号表示克罗内克积(kronecker product)；当p越大时，hp(t)对h(t)的近似程度越好，当p＝m时，hp(t)＝h(t)；

46、应用关系式

47、

48、将hp(t)写为

49、

50、其中其维数为ml×l，其维数为ml×m，il和im分别为维数为l×l和m×m的单位矩阵。

51、可选的，基于线性滤波器的近似表示对期望信号估计值的表达式进行改进的过程包括：

52、基于式(10)将期望信号x1(t)的估计值z(t)写为：

53、

54、其中，

55、

56、

57、yt,p(t)＝[yt(t)ht,1(t) yt(t)ht,2(t) … yt(t)ht,p(t)]t＝ht,p(t)y(t)

58、ys,p(t)＝[yt(t)hs,1(t) yt(t)hs,2(t) … yt(t)hs,p(t)]t＝hs,p(t)y(t)

59、ht,p(t)＝[ht,1(t) ht,2(t) … ht,p(t)]t

60、hs,p(t)＝[hs,1(t) hs,2(t) … hs,p(t)]t

61、向量/矩阵ht,p(t)，hs,p(t)，yt,p(t)，ys,p(t)，ht,p(t)及hs,p(t)的维数分别为lp×1，mp×1，mp×1，lp×1，mp×ml，lp×ml；ht,p(t)为在时域起到语音降噪作用的子滤波器向量，hs,p(t)为在空域起到语音降噪作用的子滤波器向量，ht,p(t)为在时域起到语音降噪作用的子滤波矩阵，hs,p(t)为在空域起到语音降噪作用的子滤波矩阵，yt,p(t)为经过子滤波矩阵ht,p(t)滤波后的带噪语音信号向量，ys,p(t)为经过子滤波矩阵hs,p(t)滤波后的带噪语音信号向量；

62、经过变形，z(t)表示为：

63、

64、其中，y(t)＝[y1(t) y2(t) … ym(t)]为带噪信号矩阵，vec[y(t)]＝y(t)，矩阵y(t)v(t)的维数为l×m；滤波器ht,p(t)(p＝1,2,…,p)和hs,p(t)(p＝1,2,…,p)分别在时间维度和空间维度实现降噪；

65、式(11)可进一步写为如下形式：

66、

67、其中，向量xs,p(t)＝hs,p(t)x(t)，vs,p(t)＝hs,p(t)v(t)的长度均为lp，向量xt,p(t)＝ht,p(t)x(t)，vt,p(t)＝ht,p(t)v(t)的长度均为mp，为滤波后的语音信号，为滤波后的残留噪声。

68、可选的，定义期望信号估计值的均方误差，基于线性滤波器的近似表示对所述均方误差进行变形的过程包括：

69、导出期望信号估计值z(t)的均方误差，定义z(t)的误差为

70、ε(t)＝z(t)-x1(t)  (15)

71、基于式(15)，将z(t)的均方误差定义为

72、

73、其中，

74、利用式(10)，将期望信号估计值z(t)的均方误差(16)写成

75、

76、其中，

77、

78、ρs,p(t)＝hs,p(t)ρ(t)  (19)

79、

80、ρt,p(t)＝ht,p(t)ρ(t)  (21)

81、分别固定hs,p(t)和ht,p(t)，将式(17)写成如下形式：

82、

83、

84、可选的，基于变形后的均方误差表达式获得基于克罗内克分解的迭代维纳滤波器的过程包括：

85、步骤一：将ht,p(t)的初始值设为其中，hw,p(t)为第p个通道的维纳滤波器，长为l，为矩阵ry(t)位于第(p-1)l+1至pl行及第(p-1)l+1至pl列的元素组成的矩阵，为第p个通道带噪语音信号向量的自相关矩阵，向量为向量ρ(t)的(p-1)l+1至pl个元素组成的向量，为矩阵rx(t)中位于第p行第p列的元素；

86、步骤二：应用通过公式及ht,p(t)＝[ht,1(t) ht,2(t) … ht,p(t)]t构造并将其带入至式和中，得到和上标(·)(n)表示第n次迭代的结果；

87、步骤三：将和带入至式中，得到

88、步骤四：应用通过公式及hs,p(t)＝[hs,1(t) hs,2(t) … hs,p(t)]t构造并将其带入至式和中，得到和

89、步骤五：将和带入至式中，得到

90、重复步骤二至步骤五n次，n为自由设定的参数，得到基于克罗内克分解的迭代维纳滤波器

91、本发明的技术效果为：

92、本发明通过应用奇异值分解和克罗内克分解来实现传统多通道降噪滤波器的低秩表示，将在时域维度和空域维度起降噪作用的滤波器系数分解开来，从而将一个长滤波器的估计问题转换成两个较短子滤波器的估计问题，实现基于克罗内克分解的多通道降噪方案。较短的滤波器意味着需要估计的参数变少，所以算法复杂度可显著降低。另外，估计较短的滤波器所需的信号样本数量也变少，所以降噪算法可以更好地跟踪信号统计特性的变化，更加适合处理非平稳噪声。相比传统的多通道降噪滤波器，基于克罗内克分解的多通道降噪滤波器在处理平稳噪声时，可以更加灵活地控制降噪性能和算法复杂度之间的折中；在处理非平稳噪声时，可以取得更好的降噪性能，并具有更低的复杂度；相比目前在实际系统中应用较广的频域语音降噪方法，本发明的另一个优势为不存在音乐噪声。