一种基于穆勒矩阵极分解的水下目标清晰化成像方法

本发明涉及光学成像，尤其涉及一种基于穆勒矩阵极分解的水下目标清晰化成像方法。

背景技术：

1、水下成像环境复杂，特别是在浑浊水域中，受到水体吸收和大量微粒的散射作用，目标细节信息损失严重，导致水下成像质量急剧下降，严重影响后续对水下目标的识别能力。因此，如何提高水下光学成像质量，成为浑浊水体下清晰化成像的迫切需求。

2、为了提高水下光学成像的质量，学者们提出了许多研究方法，包括：

3、1、基于图像处理的图像增强方法。该方法采用数字图像处理算法实现，虽然简单高效，但是该类算法以数据统计为基础，往往忽略掉图像质量降低的原因，处理后的图像极易导致感兴趣的细节部分模糊。

4、2、基于深度学习的偏振成像技术利用偏振信息特征提取实现清晰成像，将神经网络与偏振信息相结合，是偏振水下成像技术的新探索，此方法往往需要大量的样本数据以优化模型参数，泛化能力不强，并不适用于陌生的场景。

5、3、基于偏振成像技术的去散射方法。偏振成像技术提升了目标信息维度，是目前实现水下清晰化成像的有效方法之一。采用偏振成像去散射的方法一般有两类，第一类是将偏振度引入到水下光学成像物理模型，其核心思想是求解目标与背景的偏振度，并利用两者之间的偏振度差异实现清晰化成像，但该方法不可避免地存在偏振度的计算难题；第二类是偏振成像结合深度学习实现去散射，利用增加的偏振维度信息实现清晰成像，是偏振水下成像技术的新探索，但是该方法往往需要大量的样本数据以优化模型参数，泛化能力不强，而且很难适用于陌生场景。

6、因此，现有提高水下光学成像质量的计算方法存在偏振度的计算难、样本量要求高、参数计算难等问题。

技术实现思路

1、本发明的目的在于提供一种基于穆勒矩阵极分解的水下目标清晰化成像方法，通过穆勒矩阵极分解的方式获取退偏矩阵图像，以图像质量为目标优化水下光学成像物理模型中透射率图的估计，利用此模型反演出目标的清晰图像，无需估计目标和场景的偏振度，解决现有计算方法存在偏振度的计算难、样本量要求高、参数计算难等问题。

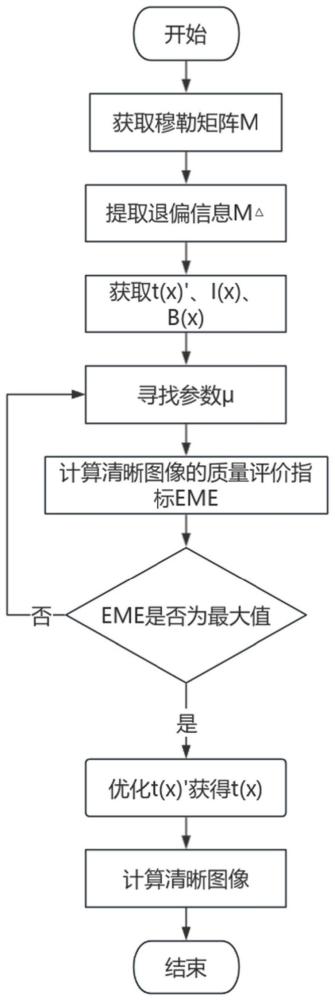
2、为达成上述目的，本发明提供一种基于穆勒矩阵极分解的水下目标清晰化成像方法，包括以下步骤：

3、步骤1、搭建穆勒矩阵水下光学成像物理模型，选取穆勒矩阵的第一个元素为总光强信号，进而根据目标场景选择无穷远处的散射光强；将穆勒矩阵极分解得到退偏图像，使用退偏图像初步估计光学成像模型的透射率图；

4、步骤2、使用一修正系数对初步估计的透射率图进行修正，以优化图像质量；

5、步骤3、选择增强度量eme作为图像质量的评价指标，使用粒子群算法遍寻修正系数，直至eme为最大值，选取eme为最大值时的修正系数对初步估计的透射率图进行修正，获得清晰图像的透射率图；

6、步骤4、根据获得的清晰图像透射率图、总光强信号和无穷远处的散射光强计算得到水下目标清晰图像。

7、进一步，在步骤4中，计算水下目标清晰图像的方法如下：

8、根据现有水下光学成像原理，水体的吸收和微粒的散射作用，探测器接受到的信号包括三个部分：

9、i(x)＝ia(x)+ib(x)+if(x)#(1)

10、式中，i(x)为探测器像素x处收到的总光强信号；ia(x)为衰减的目标信号光；ib(x)为后向散射光，是图像退化的主要原因；if(x)为前向散射光，忽略不计，ia(x)用目标的清晰图像和整个场景的透射率图表达，ib(x)用整个场景的透射率图和无穷远处的散射光强表达，由此，式(1)改写为：

11、i(x)＝iobj(x)t(x)+(1-t(x))#(2)

12、式中，iobj(x)为目标的清晰图像；t(x)为整个场景的透射率图，取值范围为0-1；b∞为无穷远处的散射光强，不同的取值会影响成像效果，b∞选择背景区域的均值，或者选择i(x)最亮的0.1％像素的均值，根据式(2)，反演出目标的清晰图像：

13、

14、进一步，在步骤1中，根据穆勒矩阵极分解的原理，一个归一化的4×4穆勒矩阵表示为三个子矩阵的乘积：

15、m＝mδmrmd#(4)

16、式中，mδ、mr、md分别代表退偏、相位延迟和二向衰减特性，穆勒矩阵中的第一个元素为总光强信号i(x)，b∞选择i(x)最亮的0.1％像素的均值，退偏矩阵mδ的表达式为：

17、

18、式中，为3×1的偏振向量，mδ是表征场景退偏信息的关键参数，表达式为：

19、

20、将mδ的元素用于估计光学成像物理模型中的透射率图t(x)′：

21、

22、式中，

23、

24、式中，将mδ平方处理是以增强对比度且不损失任何信息；将mδ最大值处理以使初步估计的透射率图t(x)′的取值范围为0-1。

25、进一步，在步骤2中，使用一修正系数μ来对t(x)′来进行修正，以优化图像质量，得到t(x)，则式(3)改写为：

26、

27、式中，μ在一个场景下为固定常数，取值范围为0-1/max(t(x))。

28、进一步，在步骤3中，eme的表达式为：

29、

30、式中，iobj(x)图像被划分为m×n块，smax；m,n和smin；m,n表示每块图像中像素灰度值的最大值与最小值，同时为了避免被零划分，参数q取接近于0的正值，设为0.0001；使用粒子群算法寻找μ，将寻找的μ值代入式(9)获得eme值，判断获得的eme值是否为最大值，若为最大值，则代入的μ值为最终选取的修正系数，若获得的eme值不是最大值，则继续寻找μ值代入式(9)中重复计算，直至获得eme的最大值。

31、进一步，在步骤1中，所述穆勒矩阵水下光学成像物理模型采用一套双dofp型穆勒矩阵成像装置搭建，所述双dofp型穆勒矩阵成像装置包括偏振态产生器、偏振态分析器、led点光源、准直透镜、带通滤光片、扩束镜，所述偏振态产生器包括一个固定角度的偏振片p和一个可旋转的1/4波片r1，所述led点光源、准直透镜、带通滤光片、p、r1、扩束镜依次排列设置在一条直线上以照射目标场景，所述偏振态分析器包括两个线偏振相机dofp1、dofp2、一个50:50的非偏振分光棱镜和一个固定角度的1/4波片r2，所述dofp1和dofp2分别固定在分光棱镜垂直的两侧，r2固定在dofp1和分光棱镜之间，以p的透光轴固定为水平方向，作为成像物理模型的基准轴，所述dofp1的相机主轴与基准轴之间具有夹角；

32、led点光源经过准直透镜和带通滤光片后形成准直单色光源，准直单色光源通过偏振态产生器和扩束镜照射目标场景，后经偏振态分析器检测，获得场景的穆勒矩阵，以斯托克斯矢量描述偏振光束，穆勒矩阵描述光学元件和被测场景，两个相机采集的8×4强度矩阵i表示为：

33、i＝apsa·m·apsg#(11)

34、式中，m代表被测场景的穆勒矩阵，apsa、apsa分别为偏振态产生器和偏振分析器的穆勒矩阵，表示为：

35、

36、式中，sled为入射自然光的斯托克斯矢量，表示为：

37、sled＝[1,0,0,0]t#(13)

38、式中"t"代表矩阵的转置运算。

39、偏振片p的方位角固定，并且整个系统以其透光轴为其基准，其穆勒矩阵mp表示为：

40、

41、mri(i∈1,2)为两个1/4波片的穆勒矩阵，参数θri,δri(i∈1,2)分别为两个波片相对于基准的方位角大小和实际延迟量大小，其穆勒矩阵表示为：

42、

43、adofp为偏振相机的穆勒矩阵，表示为：

44、

45、则被测场景的穆勒矩阵表示为：

46、

47、式中代表矩阵的伪逆运算，根据系统工作原理及仪器优化理论，需要将r1旋转至4个不同的方位角并使得apsg的条件数最小，优化得到的r1的4个不同的角度为(-45°，-19.6°，19.6°，45°)，进而通过式(12)-(17)解算出场景的穆勒矩阵m。

48、进一步，所述dofp1的相机主轴与基准轴之间的夹角为21°。

49、采用上述方案后，本发明的有益效果在于：

50、本发明通过穆勒矩阵极分解方法从归一化的穆勒矩阵中分离出介质的退偏矩阵图像，以此估计光学模型中的透射率图，并以目标图像质量为指标优化透射率图的估计，在不同散射强度和不同材料目标下得到去散射后的目标清晰图像。退偏特性是与散射介质强相关的一个参数，利用退偏信息可以表征散射介质，从而本发明无需从场景分离出目标和散射光的偏振度，降低了参数估计的复杂度，在不同散射强度对不同材质目标均呈现较好的去散射效果，解决现有计算方法存在偏振度的计算难、样本量要求高、参数计算难等问题。

51、而且，本发明还采用一套双dofp型穆勒矩阵成像装置搭建穆勒矩阵水下光学成像物理模型，缩短了4×4穆勒矩阵图像的测量时间并简化仪器运动的复杂度。

52、本发明为水下清晰化成像提供了一种新方法，有望给海洋资源开发等领域提供帮助，也可为进一步的研究提供一些启示和指导。