一种坚硬岩层-厚松散层耦合条件下地表采动程度计算方法

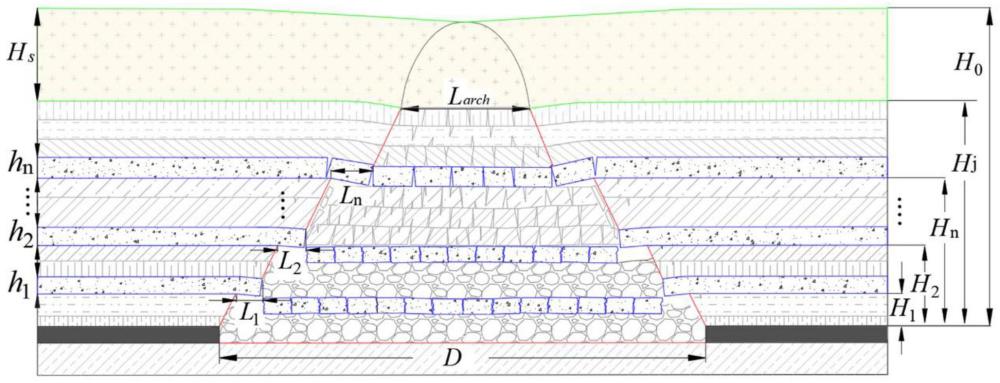
本发明涉及地表采动程度计算。具体地说是一种坚硬岩层-厚松散层耦合条件下地表采动程度计算方法。

背景技术：

1、地表沉陷是岩层损伤运移的外在表现，是地下开采导致的岩层破断不断向上传递发育的结果，其本质上是力学现象。在地表移动盆地随煤层开采而发育的过程中，一般根据采动对地表移动变形的影响，将地表采动程度分为非充分采动、充分采动、超充分采动。覆岩垮落区形态及岩层运移一定程度上决定了地表采动程度，而地表采动程度也是判断覆岩破坏程度、工作面尺寸优化、地表控制减沉的重要依据。

2、目前，关于地表采动程度的计算方法很多，主要包括：经验公式计算方法、数值模拟、物理模拟和基于松基比的计算方法。其中数值模拟和物理模拟的方法由于模型本身与实际情况存在差异，导致的计算结果误差不容忽视；而基于松基比的计算方法，虽然解决了部分模型误差的问题，但其本质上仍是数学的经验方法，未涉及力学参数，公式的应用推广上缺乏合理性，所以目前我国普遍应用的采动系数计算公式仍为《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规范》中给出的经验公式的计算方法。

3、但是现有的方法大多将覆岩均化为一类介质或仅区分松散层，利用经验系数计算地表采动程度，缺少从力学的角度，同时顾及坚硬岩层和松散层对充分性影响的方法。例如根据现场实测，当采空区长度和宽度均达或超过1.2h0～1.4h0(h0为平均采深)时，地表达到充分采动。将覆岩均化为一种介质，根据采深利用经验的方法计算工作面临界充分采动距，从而确定采动系数。但技术方案没有区分松散层与基岩区别，只根据经验利用数学的方法进行临界充分采动距离的计算。又如将覆岩区分松散层和基岩的，基于利用两种介质在采动后产生破断角大小的不同来计算工作面临界充分采动距，从而确定采动系数，该技术表明了松基比与采动程度的关系，但是其没有考虑到基岩中具有控制作用的坚硬岩层，也忽视了松散层的成拱特性。本质上没有从力学的角度来考虑采动充分性的计算问题。

技术实现思路

1、为此，本发明所要解决的技术问题在于提供一种从力学角度坚硬岩层-厚松散层耦合条件下地表采动程度计算方法，同时顾及坚硬岩层和松散层对地表采动程度的影响，依据不同坚硬岩层的破断模式及松散层垮落形态。

2、为解决上述技术问题，本发明提供如下技术方案：

3、一种坚硬岩层-厚松散层耦合条件下地表采动程度计算方法，包括如下步骤：

4、(1)确定矿区基本地质采矿参数；

5、(2)基于关键层理论确定坚硬岩层，依据坚硬岩层位置和厚度，计算硬岩断块回转量，确定坚硬岩层的破断模式；

6、(3)计算坚硬岩层悬臂梁结构的最大伸悬距离、铰接岩梁结构关键块的水平分量；

7、(4)根据松散层的内摩擦角、粘聚力等物理参数，计算松散层内的自然平衡拱宽度；

8、(5)计算坚硬岩层-厚松散层耦合条件下的工作面临界充分开采宽度d；

9、(6)基于工作面实际采宽d0，计算采动系数n，确定地表采动程度。

10、上述一种坚硬岩层-厚松散层耦合条件下地表采动程度计算方法，在步骤(1)中，矿区基本地质采矿参数，包括：采深h0、采厚m、碎胀系数kp、坚硬岩层厚度、坚硬岩层距煤层距离、坚硬岩层抗拉强度rt、松散层内摩擦角和粘聚力c。

11、上述一种坚硬岩层-厚松散层耦合条件下地表采动程度计算方法，在步骤(2)中，以第i层岩层为假定坚硬岩层，其上直至第m层岩层与之协调变形，而第m+1层岩层不与之协调变形，则第m+1层岩层是第i+1层坚硬岩层，通过如下的刚度条件和强度条件从第i层开始向上逐层进行判定：

12、刚度条件判别式如式(1)所示：

13、

14、其中，e为岩层的弹性模量；γ为岩层的容重；hi表示第i层的岩层厚度，0<i<m+1；hm+1表示第m+1层的岩层厚度；γi为第i层的岩层的容重；γm+1为第m+1层的岩层的容重；em+1为第m+1层的岩层的弹性模量；

15、强度条件判别公式如下：

16、li<lm+1                                      (2)；

17、其中，li为第i层岩层的破断距；lm+1为第m+1层岩层的破断距；

18、对覆岩的所有岩层进行判断，直到同时满足刚度条件判别式、强度条件判别式，即能确定第i层岩层为坚硬岩层；

19、坚硬岩层的破断模式主要受工作面采高、坚硬岩层位置及厚度所制约；同一工作面中，随着采空区的增大，低位坚硬岩层断块在大采高条件下的回转量超过维持其结构平衡的最大回转量，则会以“悬臂梁”模式切落；处于上部的坚硬岩层由于垮落岩体的碎胀性，破断后发生的回转量较小，形成稳定的“铰接岩梁”结构；坚硬岩层破断后呈现何种结构，根据破断块体的回转量来判断：

20、坚硬岩层与垮落堆积体之间的高度视为最大回转量δ：

21、δ＝m-∑hi(kp-1)                                (3)；

22、式中：m为煤层采厚；hi为某一层坚硬岩层与煤层的距离；kp为碎胀系数；

23、假设坚硬岩层破断块体能够形成“铰接岩梁”结构的最大回转量为δmax，则当δ>δmax时，坚硬岩层呈现“悬臂梁”切落结构；根据梁式理论得：

24、

25、式中：hi为某一层坚硬岩层厚度；q为坚硬岩层上覆载荷及自重；lc坚硬岩周期破断长度；σc为坚硬岩抗压强度；

26、则坚硬岩层“悬臂梁”切落模式形成条件为：

27、

28、若(5)式不成立，则坚硬岩层破断后形成“铰接岩梁”结构。

29、上述一种坚硬岩层-厚松散层耦合条件下地表采动程度计算方法，在步骤(3)中，

30、坚硬岩层“悬臂梁”切落模式的最大伸悬端距离lmax为：

31、

32、坚硬岩层“铰接岩梁”铰接模式关键块的水平分量l为：

33、

34、式中，rt为坚硬岩层抗拉强度，q为硬岩层上覆载荷及自重；hi为第i层坚硬岩层厚度；α为坚硬岩块回转角度。

35、上述一种坚硬岩层-厚松散层耦合条件下地表采动程度计算方法，在步骤(4)中，松散层自然平衡拱具有一定厚度，拱顶主要受到轴向压力，拱肋和拱脚受水平推力、垂直压力和弯矩共同作用；

36、为简便计算，将地表和潜在滑移面视为直线，将松散层自然平衡拱迹线近似为椭圆曲线，则松散层自然平衡拱结构矢高和跨度比值，即矢跨比满足：

37、

38、松散层自然平衡拱结构厚度为：

39、

40、当松散层自然平衡拱发育至地表时，地表达到充分采动状态，此时的松散层自然平衡拱的跨度larch表达式为：

41、

42、式中：γs为松散层容重n/m3；hs为松散层厚度/m；λ为侧压系数；为松散层内摩擦角/°；c为土体粘聚力；larch为松散层自然平衡拱的宽度/m。

43、上述一种坚硬岩层-厚松散层耦合条件下地表采动程度计算方法，在步骤(5)中，

44、确定松散层占比系数、第i层坚硬岩层占比系数、第i层坚硬岩层层位系数：

45、松散层占比系数s：

46、

47、第i层坚硬岩层占比系数pi：

48、

49、第i层坚硬岩层层位系数ci：

50、

51、自下往上第i层硬岩的载荷及自重为：

52、

53、其中，hj为覆岩除松散层之外的基岩厚度，k为最大的坚硬岩层数；γr，γy和γs分别表示软弱岩体、坚硬岩体和松散层的容重，ci表示第i层坚硬岩层层位系数；h0为采深；

54、若经过步骤(2)判别后，工作面上方有a层坚硬岩层形成“悬臂梁”伸悬结构，有b层坚硬岩层形成“铰接岩梁”结构；

55、则当i≤a时，悬臂梁伸悬端长度为：

56、

57、当a<i≤b时：铰接岩梁关键块水平分量为：

58、

59、由于岩层破断呈现两侧近似对称，工作面两侧的软弱岩层破断角及坚硬岩层破断机制近乎相同，根据公式(15)、(16)和松散层自然平衡拱宽度求取公式(10)求得地表达到充分开采程度时的工作面临界采宽d为：

60、d＝2h0[(1-s)(1-∑pi)cotβr]+2∑li+larch      (17)；

61、式中：βr为软弱岩层破断角。

62、上述一种坚硬岩层-厚松散层耦合条件下地表采动程度计算方法，在步骤(6)中，采动系数是工作面实际采宽d0与地表达到充分采动时的临界采宽d之比，充分采动角是地表移动盆地平底边缘点至采空区边界的连线与煤层在采空区一侧的夹角；

63、采动系数和充分采动角能够判断采动程度和预测地表最大下沉值出现的位置，根据建立的充分临界采宽d计算模型得采动系数n为：

64、

65、式中：d0为工作面实际采宽；

66、当走向和倾向方向采动系数n均大于等于1时，地表达到充分采动状态。

67、本发明的技术方案取得了如下有益的技术效果：

68、1、本发明提出了一种新的地表采动程度计算方法。技术关键点是根据坚硬岩层破断后悬臂长度及松散层自然平衡拱发育特征，将不同层位、不同厚度的坚硬岩层破断后形成的悬臂平衡模式分为悬臂梁和铰接岩梁，并顾及不同厚度下松散层的成拱特征，认为当采场垮落压实区高度发育至地表时，地表出现最大下沉并达到充分采动状态，提出了坚硬岩层-厚松散层耦合条件下的地表采动程度的计算方法。

69、2、深入研究坚硬岩层的悬臂长和厚松散层内自然平衡拱的发育特点，为精准预测两者耦合条件下的地表采动程度提供了新的计算方法。

70、3、本专利计算坚硬岩层-厚松散层耦合条件下的地表采动程度计算方法，相较于经验系数法、充分采动角法等，兼顾了松散层和坚硬岩层对地表采动程度的影响，从力学的角度来判断地表采动程度；相较于依靠经验系数的数学方法，其计算过程更加合理，计算结果精度更高。

71、3、保护点为：(1)松散层自然平衡拱厚度及矢跨比计算；(2)松散层占比系数、坚硬岩层占比系数、坚硬岩层层位系数的归一化确立；(3)坚硬岩层-厚松散层耦合条件下工作面临界采宽计算方法。