基于消息传递算法的宽带信号的DOA估计方法

本发明属于无线通信，尤其涉及一种基于消息传递算法的宽带信号的doa估计方法。

背景技术：

1、从第二代移动网络(2g)开始，无线定位已经是移动通信系统的重要特性，且每一代的定位精度都在不断提高。在第五代(5g)移动网络中，定位被认为是其关键特征之一，因为它是各种基于位置的服务的基础前提。虽然5g移动网络的正在逐步部署，国际电信联盟已经在“网络2030”提出第6代(6g)移动通信关键特性。同时《6g无线智能无处不在的关键驱动与研究挑战》中指出感知一体化(isac)是下一代无线通信(6g)的关键功能，是促进未来物理、生物和数字世界融合的关键赋能技术。波达角度估计(doa)不仅可以实现入射信号的方位感知，同时也是无线通信系统信道估计的重要部分，因此高精度的doa估计算法提高通信质量的同时可以更精准的感知用户。在6g系统中，将通过更高的频段(从毫米波到太赫兹)、更宽的带宽和更大的天线阵列，使射频感知和通信紧密结合，相互增强，进而降低总体成本。

2、因此高精度的宽带doa算法一直受到国内外学者和工业界的广泛关注，而现有的宽带的doa估计算法都是将窄带doa估计算法推广到宽带，他们都假设频带的占有率相同，然而这一假设是不符合实际情况。

技术实现思路

1、本发明要解决的技术问题是，提供一种基于消息传递算法的宽带信号的doa估计方法，本发明提供了一种基于消息传递算法的宽带信号doa估计方法，可应用于宽带、大规模mimo的移动通信系统中，实现高精度的方位感知和信道估计。

2、为了解决上述技术问题，本发明采用的技术方案是：该基于消息传递算法的宽带信号的doa估计方法，具体包括以下步骤：

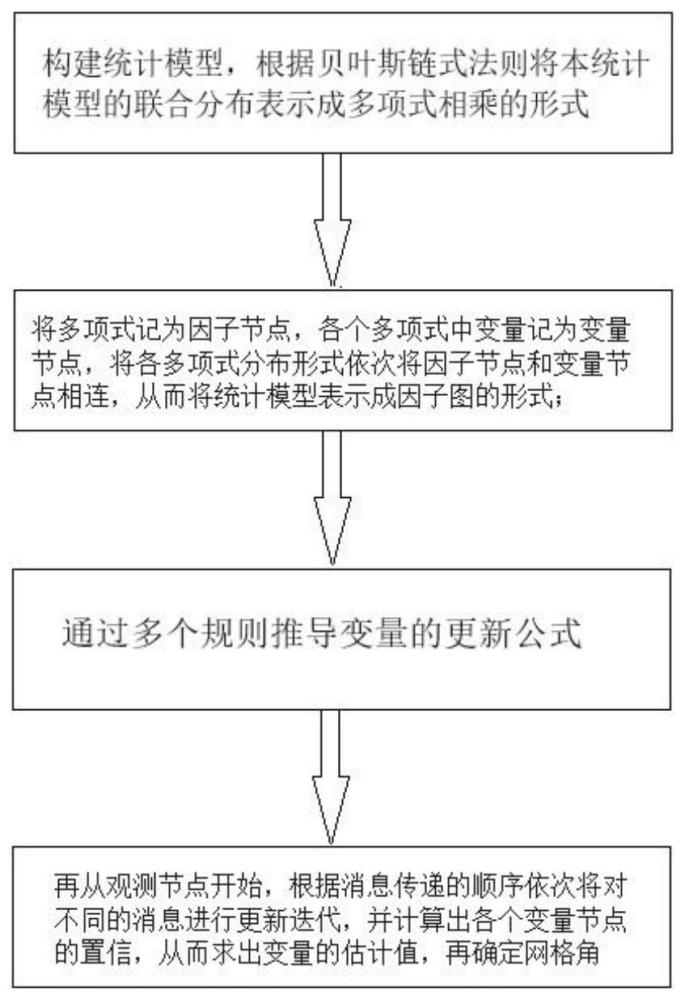
3、s1：根据信号模型构建统计模型；再根据贝叶斯链式法则将所述统计模型的联合分布表示成多项式相乘的形式；

4、s2：将所述多项式记为因子节点，各个所述多项式中变量记为变量节点，将各多项式分布形式依次将因子节点和变量节点相连，从而将统计模型表示成因子图的形式；

5、s3：通过多个规则推导变量的更新公式；

6、s4：再从观测节点开始，根据消息传递的顺序依次将对不同的消息进行更新迭代，并计算出各个变量节点的置信，从而求出变量的估计值，直至算法收敛或满足迭代终止条件，得到带估计变量的最优估计值，再根据估计值的稀疏性，确定不为零元素的位置从而确定所对应的网格角，提高doa估计精度。

7、采用上述技术方案，首先根据入射信号的特点建立稀疏信号统计模型，其次对统计模型中变量用因子图表示，然后bp、ep、mf多种规则得到位置变量的更新公式；其中将统计模型表示成因子图，从图子图中可知各因子节点的和变量节点的具体关系和概率密度函数的分布形式，从而对不同消息节点的进行划分，采用不同的消息传递规则计算出各节点的消息，最后从观测开始，根据消息传递的方向，依次按各消息的迭代更新顺序进行迭代更新，从而设计出高精度的doa估计算法。本发明充分发挥了各规则的优点，提升算法估计精度的同时保证算法的收敛性。

8、优选地，所述步骤s1中的信号模型为宽带信号模型，表示为：

9、

10、其中，n为过完备字典的网格划分数，m为ula阵列的传感器个数，f为接收信号时通过dft转换为频域信号后的子带个数，yf∈cm×1为观测数据，为过完备字典的一阶近似af是网格字典，bf为af的导数，δf＝diag(βf)是真实角度与网格的偏差βf构成的对角矩阵，xf∈cn×1为信源的幅值向量，c是复数集合，wn为复高斯噪声。

11、优选地，所述步骤s1中根据信号模型构建统计模型具体为：wf∈cm×1服从精度为α0的复高斯噪声，c是复数集合，似然函数表示为α0服从参数为a，b的gamma分布记为xf服从精度矩阵为λf＝diag(αf)，αf服从参数为c，d的gamma分布记为{αf}f＝1：f服从g分布，g是参数为γ，g0的狄利克雷过程dp(g|γ，g0)的一个随机测度，采用截法得到其中，πk服从beta分布记为γ服从参数为e，h的gamma分布记为分配向量zf服从多项式分布当xf的条件概率分布为其中1{zf＝k}表示xf第k类时zf的第k个位置值为1其余为0，

12、优选地，所述步骤s1中根据贝叶斯链式法则将所述统计模型的联合分布p({yf}f＝1：f，θ)表示成多项式相乘的形式，公式为：

13、

14、其中，是统计模型的隐含变量，其中超参数集合{a，b，c，d，e，h}均为大于零较小值。

15、优选地，所述步骤s2中将统计模型的因子图表示具体为：将所述统计模型的多项式分布中的变量和分布分别用变量节点和因子节点表示，并将因子节点和变量节点相连构成因子图。

16、优选地，在所述步骤s3中分别基于mf规则、bp规则和ep规则及融合所述mf规则、bp规则和ep规则进行变量公式的推导。

17、优选地，所述步骤s3中基于消息传递算法的各变量为循环迭代更新，此次迭代默认为上次迭代结果已知，且当前变量更细，默认其他变量不变；具体步骤为：

18、s31：通过mf规则获得稀疏信号xf的更新公式，表示为：

19、

20、

21、

22、其中，φf，k是配向量zf的期望值，γf是xf的精度值，uf是xf的期望值；

23、s32：通过mf规则获得中间变量参数的更新公式，表示为：

24、

25、其中，δf，i为γf对角线的第i个元素，uf，i为向量uf的第i个元素；

26、s33：通过bp-mf规则推导得出分配变量的更新公式，表示为：

27、

28、

29、

30、其中，δk＝diag(βk)；

31、s34：通过mf规则得到离散程度参数γ的更新公式，表示为：

32、

33、s35：通过ep-bp-mf规则得到截棍定理变量πk的更新公式，表示为：

34、

35、其中，

36、

37、

38、归一化常数表示为：

39、

40、

41、

42、s36：通过mf规则得出噪声精度α0的更新公式，表示为：

43、

44、s37：通过em规则得出离网偏差βk的更新公式，表示为：

45、

46、

47、上述公式为循环迭代更新本次迭代默认上次迭代中已经给出，例如步骤s31中的φf，k在步骤s33中给出了，步骤s33中πk′的更新则在步骤s35中给出；其中已知变量只有{yf，af，bf}f＝1：f，其余均为中间变量即隐藏变量。

48、优选地，所述步骤s4具体为：所述步骤s4具体为：输入观测值yf，af，bf，设置算法的迭代终止条件thr和最大迭代次数itmax，初始化隐含变量θ和超参数{a，b，c，d，e，h}；从观测节点开始，根据消息传递的顺序依次将对不同的消息进行更新迭代，并计算出各变量节点的置信，即依次得到xf更新值、更新值、更新值、πk更新值、γ更新值、α0更新值和βk更新值，直至算法收敛或满足迭代终止条件，从而求出{xf}f＝1：f变量的估计值；即得到xf最优估计值，再根据{xf}f＝1：f的稀疏性，确定不为零元素的位置从而确定所对应的网格角，并补全βk离网角度，提高doa估计精度。

49、与现有技术相比，本发明具有以下有益效果：首先根据入射信号的特点建立稀疏信号统计模型，其次对统计模型中变量用因子图表示，然后bp、ep、mf多种规则得到位置变量的更新公式；其中将统计模型表示成因子图，从图子图中可知各因子节点的和变量节点的具体关系和概率密度函数的分布形式，从而对不同消息节点的进行划分，采用不同的消息传递规则计算出各节点的消息，最后从观测开始，根据消息传递的方向，依次按各消息的迭代更新顺序进行迭代更新，从而设计出高精度的doa估计算法。本发明充分发挥了各规则的优点，提升算法估计精度的同时保证算法的收敛性。