一种基于路端相机及车端IMU数据融合的车路协同定位方法

本发明涉及计算机视觉领域，具体是一种基于路端相机及车端imu数据融合的车路协同定位方法。

背景技术：

1、科学技术的进步不断推动着汽车的智能化发展，高精度定位是汽车智能化发展中的重要一环。对于智能汽车，高度精确的位置信息是其感知交通状况，规划行驶路径，决策行驶行为的前提。作为自动驾驶系统正常运行的基础，随着自动驾驶技术的持续发展和普及，智能汽车高精度定位的需求日益增加。目前，智能汽车高精度定位主要依赖于卫星导航系统(如gps、北斗等)、惯性导航系统、车载传感器和高精度地图等技术的综合应用。

2、卫星导航系统是目前智能汽车定位最方便快捷的手段，通过接收卫星信号，车辆可以确定自身的经纬度和高度信息，从而实现在地图上的定位。然而，由于卫星信号在高建筑物密集的区域存在峡谷效应，容易受到影响，在隧道等区域还存在信号盲区，限制了定位的精度和范围。因此，惯性导航系统和车载传感器等技术常与卫星导航一起应用以弥补卫星定位的不足。惯性导航系统通过测量车辆行驶时的加速度和角速度等信息来估计车辆的运动状态，从而辅助卫星导航系统提供更精准的定位信息。同时，车载传感器也可以收集车辆周围的环境信息，如道路条件、交通情况等，为定位提供更多的参考数据。此外，高精度地图也是智能汽车高精度定位不可或缺的一部分，高精度地图可以提供道路的详细信息，包括车道线、交通标识、交叉路口结构等，为自动驾驶车辆提供精准的位置参考和路径规划，从而提高定位精度和行驶安全性。除了一些车辆自定位手段以外，车路协同的定位方式也在不断发展成熟。车路协同定位技术基于车辆和道路基础设施之间的信息交互，实现高精度定位。在车路协同定位中，车辆利用车载传感器如相机、雷达等获取周围环境信息，并通过车载通信技术，将这些信息传输给路端基站，路端基站可以利用收到的车辆信息，结合本地的传感器数据和高精度地图信息，对车辆位置进行校正和验证，从而提供更准确的位置信息反馈给车辆。

3、以上定位方法，卫星导航在信号盲区无法使用，而车载惯性导航系统长时间运行会产漂移，而基于通信的车路协同定位成本过高。因此，本文研究旨在在卫星信号定位盲区提供一种低成本，高精度的定位方案。研究通过在智能汽车上装载惯性导航系统以及信标，在路侧以固定间距安装单目相机，利用惯导系统为路侧相机单元提供运动信息，路侧相机单元利用该信息构造虚拟运动，并结合相机对车载信标的观测信息，矫正惯导系统的漂移，实现对智能汽车的高精度定位。

技术实现思路

1、发明目的：针对现有技术中存在的不足，本发明提供了一种基于路端相机及车端imu数据融合的车路协同定位方法，以解决上述背景技术中所提到的问题。

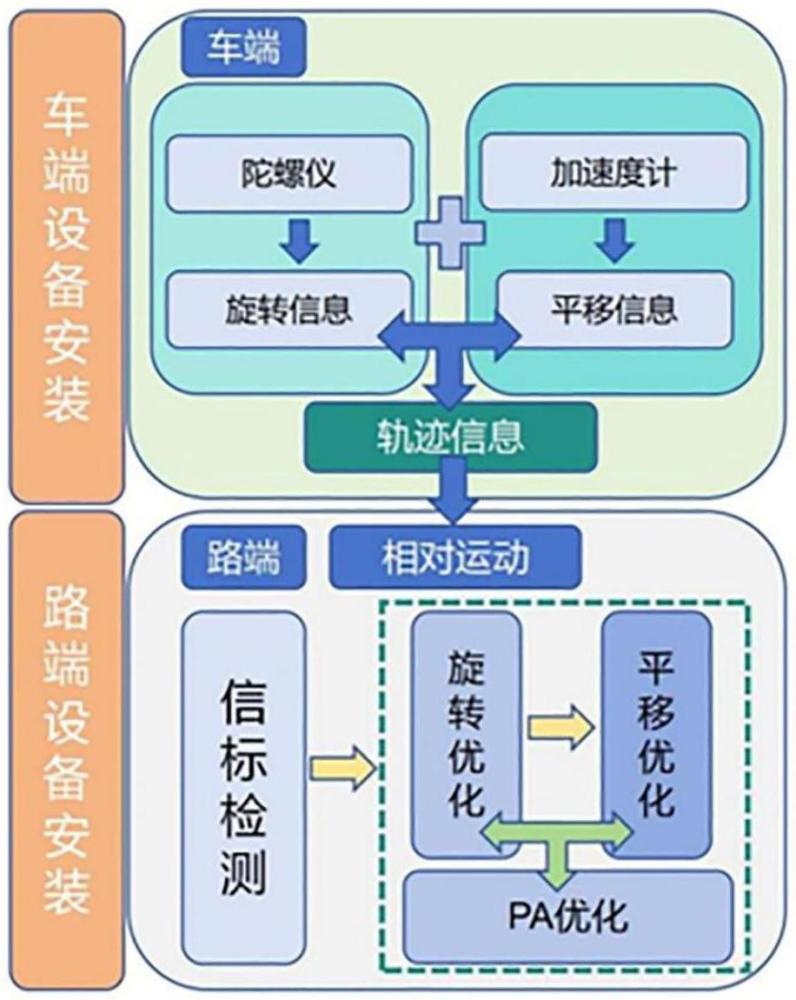
2、技术方案：一种基于路端相机及车端imu数据融合的车路协同定位方法，步骤包括：

3、s1.车端信标安装以及imu惯性测量单元数据获取、图像数据采集；

4、s2.车端信标检测与特征点提取；

5、s3.将旋转优化问题转化为极外共面约束问题，利用各对应特征点极平面法向量共面约束构建约束方程，消除陀螺仪偏置影响，得到更精确的旋转信息；

6、s4.基于ligt算法(全局位移线性求解，linear global translation)，利用各特征点构建深度-位姿约束，去除imu加速度中的重力向量影响，得到更精确的平移信息；

7、s5.利用pa仅位姿优化算法进一步优化上述步骤得到的旋转和平移。

8、所述s1具体为：

9、在车辆顶部安装球形信标，信标与车顶之间通过螺纹杆连接，信标安装位置应互不遮挡；

10、在路端以固定间距2m～4m以及固定高度1.5m～2m，架设单目相机，采集图像数据时，车辆以50km/h匀速通过，路段相机以固定频率30hz采集图像；imu数据由车载ins惯性导航系统系统提供，该系统提供3自由度的加速度信息ɑ以及3自由度的角速度信息ω，旋转以及平移均可以通过上述信息积分得到，i时刻与j时刻之间的imu积分运动模型如式(1)所示：

11、

12、式中，r为当前时刻的旋转信息，p为当前时刻的位移信息，v为当前时刻的速度信息，dt为imu相邻测量数据的间隔时间，α,β,γ分别为平移，速度以及旋转的预积分，可由式(2)求得：

13、

14、式中，ɑk和ωk分别为k时刻加速度计以及陀螺仪的测量值。

15、所述s2具体为：

16、使用深度学习方法检测信标，并基于roi分割以及圆拟合获取信标圆心，得到特征点并赋上id；

17、使用yolov5检测车端信标，预先在多场景包括校园场景、地下停车场和实验楼下采集车端信标照片制作数据集并送入神经网络训练得到训练好的模型，路端相机在采集得到图像后，将图像送入yolov5网络检测，输出的图像中使用目标框框出了各信标的图像位置；

18、对图像中的各目标框进行roi感兴趣区域分割，在每个区域中进行自适应canny边缘检测，将检测到的轮廓进行最小二乘圆拟合，输出精确的圆心作为该图像的特征点。

19、所述s3具体为：

20、一个空间三维点xw＝(xw,yw,zw)t在相机第i帧中的观测向量可以用归一化图像坐标来表征，定义ri和ti为相机拍摄第i帧图像的全局旋转和平移，则归一化图像坐标xi可以由式(3)求得：

21、

22、式中，为第i帧中三维特征点的相机坐标，为对应特征点的深度信息，k为相机的内参数矩阵，为第i帧图像中对应特征点的像素坐标；

23、两不同位姿的相机中心以及观测到的每个空间三维点可以构成一个平面，该平面称为极平面，由这样的两个相机中心以及一组空间三维点的观测构成了一组相交于相机中心平移线的极平面集合，这些极平面的平面法向量都垂直于相机中心平移线，在以同一相机中心为端点时，这些平面法向量共面；式(4)和式(5)给出了相机纯平移情况下的极平面法向量以及旋转情况下的极平面法向量：

24、ni＝xi×x′i   (4)

25、ni＝xi×rx′i   (5)

26、式中，xi为前一帧中相机对空间三维点的观测向量，x′i为后一帧中相机对空间三维点的观测向量；

27、所述极平面法向量ni的集合构成了共面性约束，可以将n个法向量堆叠成一个3×n的矩阵n，两不同相机位姿之间可以通过最小化nnt的最小特征值实现旋转的优化，如式(6)所示构建矩阵m：

28、

29、矩阵m是3×3的实对称正定矩阵，是关于相机两不同位姿之间的旋转r的函数；

30、令λmmin为矩阵m的最小特征值，则旋转的优化问题最终可以表示为：

31、

32、该步骤中，用车端信标表征空间三维点，通过归一化这些空间三维点的相机坐标得到观测向量fi和f′i；

33、迭代优化的旋转r的初始值由imu提供的轨迹信息根据式(1)和式(2)计算得出，根据相对运动原理，对于固定着的相机和运动着的车辆，车辆的轨迹信息取逆并乘上imu与相机的初始旋转外参rbc，即可假设相机的运动，即图像序列是由车辆固定而相机运动所拍摄的，因此，图像序列各帧的旋转由imu测量数据根据式(1)计算再得到；考虑陀螺仪偏置对旋转预积分的影响，通过用一节泰勒展开近似：

34、

35、式中，bg为陀螺仪偏置，为旋转预积分对bg求导的雅可比矩阵；

36、图像序列各帧的旋转实际是imu积分出的旋转取逆再通过相机与imu之间的旋转外参rbc计算得到，将式(8)带入式(6)可以构建关于bg的矩阵m，如式(9)所示：

37、

38、最终，可以根据式(10)求解出最优bg：

39、

40、求解出的bg用于消除积分时陀螺仪偏置的影响，使得重新计算出的旋转信息更加精确。

41、所述s4具体为：

42、对于空间中的任意一对由相机拍摄的图像帧framei和framej，空间三维点在这两帧图像的成像转换方程可以由式(11)表示：

43、

44、式中，rij为framei和framej之间的旋转，tij为framei和framej之间的平移；

45、在式(11)左右两侧左乘反对称矩阵[xj]×并数值化，可以得到深度信息用di(i,j)表示：

46、

47、式中，θij＝‖[xj]×rijxi‖，同理，在式(11)左右两侧同时左乘反对称矩阵[rijxi]×并数值化，可以得到深度信息用dj(i,j)表示：

48、

49、将式(13)带入式(11)：

50、dj(i,j)xj＝di(i,j)rijxi+tij   (14)

51、式(14)为二视图成像几何的纯位姿约束方程，该方程对空间中的任意图像对均成立，且对于第k帧图像，有：

52、

53、式(15)为第i帧图像上的空间三维特征点的深度相等约束，对于空间中的n帧图像，存在个纯位姿约束以及个深度相等约束，

54、综上，基于一对左右基图像帧framel和framer，可以定义任一空间三维特征点的深度-位姿约束集合：

55、d(l,r)＝{di(l,i)xi＝dl(l,r)rlixl+tli|1≤i≤n，i≠l}

56、(16)

57、由于深度信息与图像帧间的平移线性相关，在已知各图像帧旋转的情况下，可以求解各图像帧的平移，对式(16)中的约束方程左右两侧同乘[xi]×：

58、[xi]×(dl(l,r)rlixl+tli)＝0，1≤i≤n，i≠l   (17)

59、式中，dl(l,r)与图像帧间相对平移有关，结合相对平移与全局平移的关系，可以将式(17)改写为求解全局平移的线性齐次方程：

60、btl+cti+dtr＝0，1≤i≤n，i≠l   (18)

61、式中，b＝[xi]×rlixl([rlrxl]×xr)t[xr]×rr，c＝θij2[xi]×ri，d＝-(b+c)，对于n帧图像的全局平移求解问题，用表示各图像帧的全局平移，利用空间中你的所有三维特征点构造求解方程，将式(18)改写如式(19)所示：

62、l·t＝0   (19)

63、式中，l是由全局旋转和归一化图像坐标组成的矩阵；

64、在imu的积分过程中，位移的状态变化可以由式(1)表示，该运动方程中包含了速度和重力向量；

65、利用相对运动构造相机各帧的虚拟运动，且imu与相机的平移外参对系统的影响是线性的，因此图像各帧的全局平移与imu的全局平移之间可以通过旋转外参rbc转换以实现数据融合的目的，并将式(1)带入式(19)，可以得到用于求解初速度和重力向量的方程，如式(20)所示：

66、

67、式中，a1＝-(bdt1r+cdt1i+ddt1l)，d＝bp1r+cp1i+dp1l；

68、在求解得到初始速度以及重力向量后，将加速度去除重力向量的影响，并根据初始速度重新计算各帧速度以及位移。

69、所述s5具体为：

70、根据式(16)的约束，空间三维特征点的重投影误差可以表示为：

71、

72、式中，在整个最小化重投影误差过程中，未知参数仅由相机位姿组成，即位姿优化(pa)。

73、有益效果：本发明使用车端imu和路端相机进行车路协同定位，简化了车路协同定位方案。

74、为保证车端信标检测的鲁棒性，使用基于深度学习的信标检测算法，通过网络训练后可以应用于各类场景，相比于传统的检测方法，适用性更强，检测精度也更高。

75、将旋转优化问题转化为极平面法向量共面约束问题，并由imu提供旋转优化初值，精度高，收敛快，且避免了运动恢复结构(sfm)过程。

76、使用ligt算法，将imu运动方程与之融合，去除了imu加速度中重力向量的影响，使得imu积分更加精确。

77、将旋转和位移进行pa优化，提高了位姿精度，并减少了计算时间。