一种带间隙折叠舵的超声速飞行器的气动弹性建模方法

本发明涉及飞行器设计与气动弹性分析，具体涉及一种带间隙折叠舵的超声速飞行器的气动弹性建模方法。

背景技术：

1、由于折叠舵在设计制造的过程中存在配合公差和加工精度，以及在飞行过程中存在长时间振动和磨损，折叠舵轴与舵面的铰接处会产生间隙，从而使连接处的接触刚度表现为非线性，对折叠舵面结构的动力学特性产生显著影响。

2、随着现代飞行器的设计、装备及任务逐渐复杂化、综合化，飞行器结构系统的重量不断减轻、刚度不断降低，由间隙等因素引发的非线性气动弹性问题日渐突出，其引发的极限环特性复杂、难以预测，且对飞行器影响重大。

3、中国发明专利cn105547618a公开了一种基于折叠舵面舵系统的模态分析方法，采用模态试验分析方法针对实物进行现场测试来评估舵面间隙非线性带来的影响，但是该方法并不能适用于折叠舵结构中含有线性环节的场景。

4、中国发明专利cn114996951a公开了一种基于连接界面自由度缩聚原理的连接结构降阶建模方法，将自由度缩聚结合动态子结构方法以建立系统的动力学降阶模型，但该方法只能减少连接界面的自由度，无法对整体结构进行降阶。

5、因此，需要提供一种含间隙非线性环节的折叠舵时域超声速气动弹性响应计算方法。

技术实现思路

1、鉴于上述问题，本发明提供了一种带间隙折叠舵的超声速飞行器的气动弹性建模方法，克服含间隙非线性的折叠舵面超声速气动弹性分析中理论分析方法不完善、已有算法的计算效率难以满足时域响应计算需要的问题，该方法通过自由界面模态综合法求解折叠舵的结构模型，大大减小动力系统的自由度，并将非线性引入线性结构，从而解决了折叠舵存在结构非线性环节带来的问题；基于形态插值理论和三维活塞理论，得到带间隙折叠舵的全耦合气动弹性方程，进而通过时域积分求解结构响应。

2、本发明提供了一种带间隙折叠舵的超声速飞行器的气动弹性建模方法，包括：

3、步骤1、按照折叠关系将折叠舵划分成第一子结构和第二子结构；设置第一、二子结构的连接方式，所述第一、二子结构通过多个连接点连接，基于所述连接方式获取所述多个连接点的间隙大小；

4、基于所述第一、二子结构、连接方式以及多个连接点的间隙大小构建折叠舵结构模型；如图2；

5、步骤2、基于所述折叠舵结构模型以及非线性双协调自由界面动态子结构法建立折叠舵非线性降阶模型；

6、优选的，建立所述折叠舵非线性降阶模型具体步骤包括：

7、21、基于所述折叠舵结构模型分别获取折叠舵结构模型的第一、二子结构对应的质量阵、刚度阵、线性模态阵以及第一、二子结构之间的对接关系；

8、22、将所述第一、二子结构质量阵、刚度阵和线性模态阵以及第一、二子结构之间的对接关系依据非线性双协调自由界面动态子结构法建立折叠舵非线性降阶模型；

9、进一步的，所述折叠舵非线性降阶模型的表达式为：

10、

11、

12、

13、其中，md为折叠舵广义质量阵，为折叠舵独立广义坐标对时间的二阶导，kd为折叠舵广义刚度阵，k为折叠舵子结构之间的间隙刚度，为折叠舵独立广义坐标，为折叠舵多个子结构对应的线性模态阵，由折叠舵的第一、第二子结构分别对应的线性模态阵组成，为结构外载荷，为折叠舵多个子结构对应的质量阵，由第一、第二子结构分别对应的质量阵组成，d为独立广义坐标到非独立广义坐标的坐标变换阵，为折叠舵多个子结构对应的刚度阵，由第一、第二子结构分别对应的刚度阵组成，t为转置。

14、步骤3、基于所述折叠舵非线性降阶模型和所述折叠舵结构模型得到位移插值矩阵，基于所述位移插值矩阵得到折叠舵气动模态；通过所述折叠舵气动模态获得折叠舵的结构有限元；

15、优选的，步骤3所述得到折叠舵的结构有限元具体步骤包括：

16、步骤31、基于所述折叠舵结构模型获得壁面气动网格，获取所述壁面气动网格的气动界面；

17、步骤32、利用步骤22所述折叠舵非线性降阶模型生成折叠舵的结构界面；

18、步骤33、所述结构界面和气动界面利用形态插值算法得到结构界面和气动界面之间的位移插值矩阵；

19、步骤34、利用步骤21所述第一、二子结构对应的线性模态阵与所述结构界面和气动界面之间的位移插值矩阵得到折叠舵气动模态；

20、步骤35、通过所述折叠舵气动模态得到折叠舵的活塞气动力，如图3，将步骤33所述结构界面和气动界面之间的位移插值矩阵转置得到载荷插值矩阵；通过所述折叠舵的活塞气动力和所述载荷插值矩阵得到折叠舵的结构有限元，如图4。

21、进一步的，步骤34所述折叠舵气动模态φa表达式为：

22、

23、

24、其中，φa为折叠舵气动模态，h为折叠舵多个子结构对应的线性模态阵，由折叠舵的第一、第二子结构分别对应的线性模态阵组成，为位移插值矩阵；αg为第一子结构对应的位移插值，βg为第二子结构对应的位移插值；αh为第一子结构对应的部件线性模态阵，βh为第二子结构对应的部件线性模态阵。

25、进一步的，步骤35所述折叠舵的结构有限元表达式为：

26、

27、

28、其中，为折叠舵的结构有限元，为载荷插值矩阵，为折叠舵的活塞气动力，αfa为第一子结构对应的活塞气动力，βfa为第二子结构对应的活塞气动力。

29、步骤4、基于步骤3所述位移插值矩阵得到折叠舵的气动力影响系数；

30、将所述气动力影响系数结合步骤2所述折叠舵非线性降阶模型和步骤3所述结构有限元构造全耦合的气动弹性动力学模型；

31、优选的，步骤4构造所述全耦合的气动弹性动力学模型，步骤如下：

32、步骤41、基于所述折叠舵结构模型获得壁面气动网格；所述壁面气动网格具有多个网格，计算每个网格的下洗速度；

33、步骤42、获取每个网格的来流密度、声速以及网格面积；根据所述每个网格的下洗速度、来流密度、声速以及网格面积计算每个网格的压强和气动力，得到多个网格的压强和气动力；

34、基于所述每个网格的压强和气动力得到折叠舵壁面气动网格的气动力；

35、步骤43、将步骤42中多个网格的气动力进行排序，获得排序后的气动力；

36、步骤44、将所述排序后的气动力定义为折叠舵的结构状态量，将所述折叠舵的结构状态量表征为折叠舵的气动力影响系数；

37、步骤45、利用所述气动力影响系数结合步骤2所述折叠舵非线性降阶模型和步骤3所述结构有限元构造全耦合的气动弹性动力学模型；

38、进一步的，步骤41所述每个网格的下洗速度表达式为：

39、

40、其中，wb为第b个网格的下洗速度，b＝1,2,3…b，b表示网格总数；n为气动面法向，v为来流速度矢量，wb为第b个网格的网格心的位移，x为全局坐标系的x坐标轴方向，y为全局坐标系的y坐标轴方向，z为全局坐标系的z坐标轴方向；ξ为气动网格局部坐标系的切向，vξ为来流速度v在气动网格局部切向上的分量。

41、进一步的，步骤42所述每个网格的气动力表达式为：

42、

43、其中，fb为第b个网格的气动力，ρb∞为第b个网格的来流密度,ab∞为第b个网格的声速，sb为第b个网格的面积。

44、进一步的，步骤43所述排序后的气动力表达式为：

45、

46、其中，fb为排序后的第b个网格的气动力；a0为广义速度对应的气动力影响系数矩阵，a1为广义位移对应的气动力影响系数矩阵，t为转置；为折叠舵独立广义坐标，为折叠舵独立广义坐标对时间的一阶导。

47、进一步的，步骤44所述全耦合的气动弹性动力学模型的表达式为：

48、

49、其中，为折叠舵结构状态量对时间的一阶导，即折叠舵第一、二子结构的速度和加速度，折叠舵结构状态量为折叠舵第一、二子结构对应的位移和速度；ι为单位向量；e为折叠舵结构状态量，即折叠舵第一、二子结构的位移和速度；m为折叠舵结构质量阵。

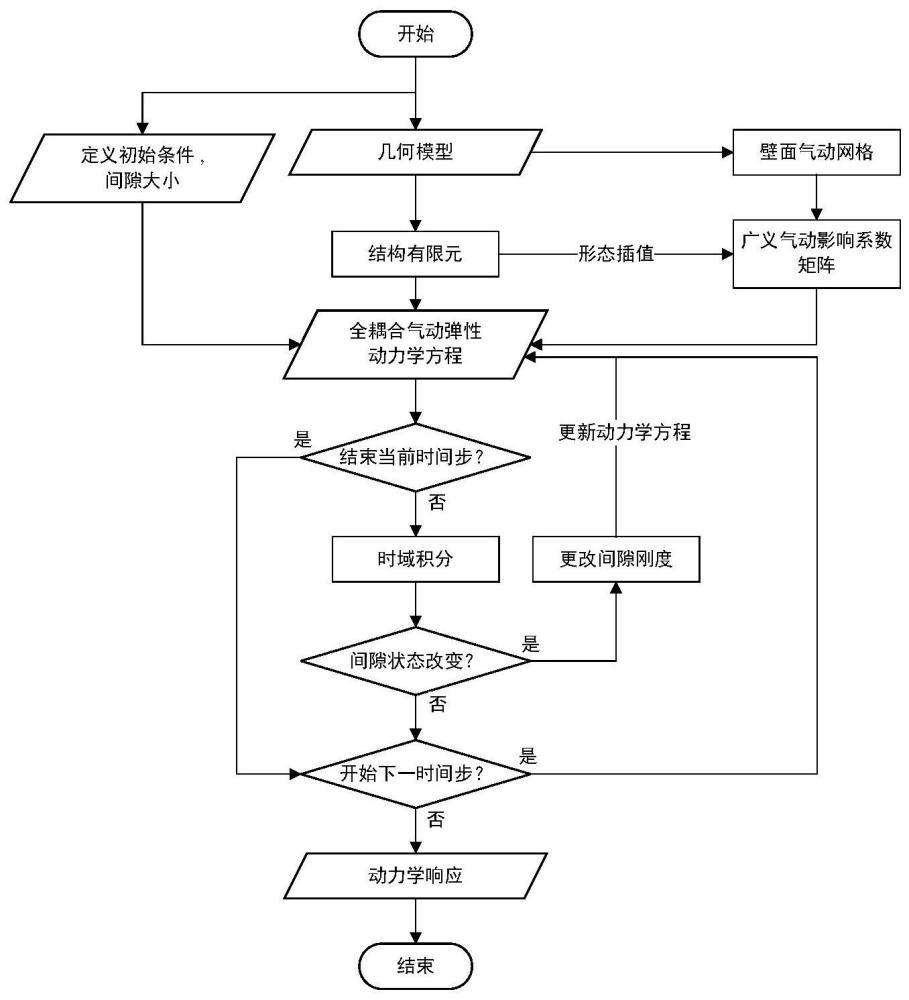
50、步骤5、基于所述全耦合的气动弹性动力学模型获得折叠舵随时间变化的位移响应曲线和速度响应曲线。

51、优选的，获得折叠舵随时间变化的位移响应曲线和速度响应曲线，具体步骤包括：

52、步骤51、预设间隙宽度；所述预设间隙宽度为折叠舵第一、二子结构连接点处的间隙宽度；

53、步骤52、令t＝0，当t＝0时为初始时刻，获取t时刻折叠舵第一、二子结构的位移和速度；

54、步骤53、基于预设间隙宽度和t时刻折叠舵的第一、二子结构的位移判断当前时刻折叠舵的第一、二子结构是否接触，若未接触，继续步骤54，若接触，则更新t时刻折叠舵的第一、二子结构的间隙刚度，得到更新间隙刚度，基于所述更新间隙刚度获得t时刻第一、二子结构更新位移，继续步骤54；

55、步骤54、将所述t时刻折叠舵第一、二子结构的位移和速度输入所述全耦合的气动弹性动力学模型，输出t时刻折叠舵的第一、二子结构的速度和加速度；

56、步骤55、比较t与t的大小，t表示时刻总个数，若t＜t，对数值t加1，并返回步骤53，获得t+1时刻的折叠舵的第一、二子结构的速度和加速度；若t＝t，则停止计算，获得t个时刻折叠舵第一、二子结构的速度和加速度；

57、基于t个时刻折叠舵第一、二子结构的速度和加速度构建折叠舵随时间变化的位移响应曲线和速度响应曲线，如图5所示。

58、进一步的，步骤53的具体步骤包括：获取t时刻折叠舵的第一、二子结构相对位移的绝对值，判断所述第一、二子结构相对位移的绝对值是否小于预设间隙宽度，若小于，则表示第一子结构和第二子结构未发生接触；若大于等于，则表示第一子结构和第二子结构发生接触，依据结构间隙的刚度-位移曲线将当前时刻折叠舵的第一、二子结构的间隙刚度进行更新，得到更新间隙刚度，基于所述更新间隙刚度获得t时刻第一、二子结构更新位移，继续步骤54。

59、与现有技术相比，本发明至少具有现如下有益效果：

60、本发明将折叠舵整体结构按照折叠关系划分成两个子结构，通过自由界面模态综合法求解折叠舵的结构模型，大大减小动力系统的自由度，并将非线性引入线性结构，有效解决了折叠舵操纵面间隙带来的间隙非线性问题，适用于折叠舵时域超声速气动弹性响应分析研究的快速应用。