一种多尺度优化设计三维点阵结构的方法

本发明涉及面向增材制造的结构多尺度优化设计，尤其涉及一种多尺度优化设计三维点阵结构的方法。

背景技术：

1、点阵结构由于能保证结构轻量化、多功能性与高可设计性等特征，在航天器结构设计中的应用受到关注。然而，目前大部分的结构设计方法只专注于宏观结构的拓扑优化、形状优化或者尺寸优化，因此在工程应用中能同时优化宏观拓扑结构及其微观结构构型的设计方法备受关注，以使设计结构的性能达到最佳。因此，发明一种能同时优化设计宏微观尺度的点阵层级结构的优化设计方法十分必要。

2、近年来，许多学者对点阵结构的优化设计进行了广泛的研究。wu等人在“computermethods in applied mechanics and engineering”期刊上发表了《topologyoptimization of hierarchical lattice structures with substructuring》,2019,345:602-617，开发了一种带有惩罚的简化子结构近似模型来映射微观尺度点阵单胞，通过减少单元的自由度来减少了点阵结构有限元的计算量，基于该模型设计了一种设计分层点阵结构的拓扑优化方法。cn202111001817.7，公开了一种基于水平集的变密度方法，通过设置设计点和定义权重系数，结合径向基函数得到水平集函数，进而计算单元密度和单元杨氏模量，建立刚度矩阵。以柔度最小化为优化目标，通过梯度约束定义点阵结构优化设计问题，最终得到单胞连续性好的最优点阵结构。

3、上述多尺度设计方法基于宏观结构由单一的微观结构构成这一假设，虽然这些方法具有计算成本较低的优点，但它们的设计空间存在局限，这限制了结构和材料的潜在能力，导致设计结构的性能无法达到最优。一些研究人员发现与均匀单胞结构相比，具有非均匀点阵微观结构的层级结构可以获得更好的性能。m.r.costa等人在“compositestructures“期刊上发表了《multi-scale and multi-material topology optimizationof gradient lattice structures using surrogate models》,2022,289:115402，提出了一种两尺度并行优化点阵结构的方法，通过同时进行宏观结构和基本材料微结构的拓扑优化来实现最佳拓扑结构。zhou等人在“computer methods in applied mechanics andengineering”期刊上发表了《multi-scale and multi-material topology optimizationof channel-cooling cellular structures for thermomechanical behaviors》,2021,383:113896，提出了一种并发的多尺度和多材料拓扑优化方法，用于设计包含冷却通道的多胞结构，以实现有效的热屏蔽和承载能力。cn202111575942.9，提供了一种微观尺度上的建模分析和宏观尺度上的节点密度优化算法，通过相对密度分布和杆件长细比的关系，获取杆件平均长细比分布，并生成点阵/多孔结构的几何构型，克服了传统规则点阵结构的各向异性和载荷敏感性问题，可应用于工程结构的轻量化设计。

4、目前大部分研究只研究了二维点阵单胞结构和点阵微观结构单参数优化，这限制了点阵结构多尺度设计在工程领域的应用。而三维点阵结构的多尺度优化方法中往往采用宏观尺度与微观尺度同步优化，这导致了计算成本过大。除此之外，最常用的制造点阵结构的增材制造工艺容易在单胞支柱等材料密度较小的位置出现制造缺陷，导致制造出的结构性能达不到理论设计性能。因此，需要考虑现有技术所存的问题，实现新型点阵材料结构的多尺度优化。

技术实现思路

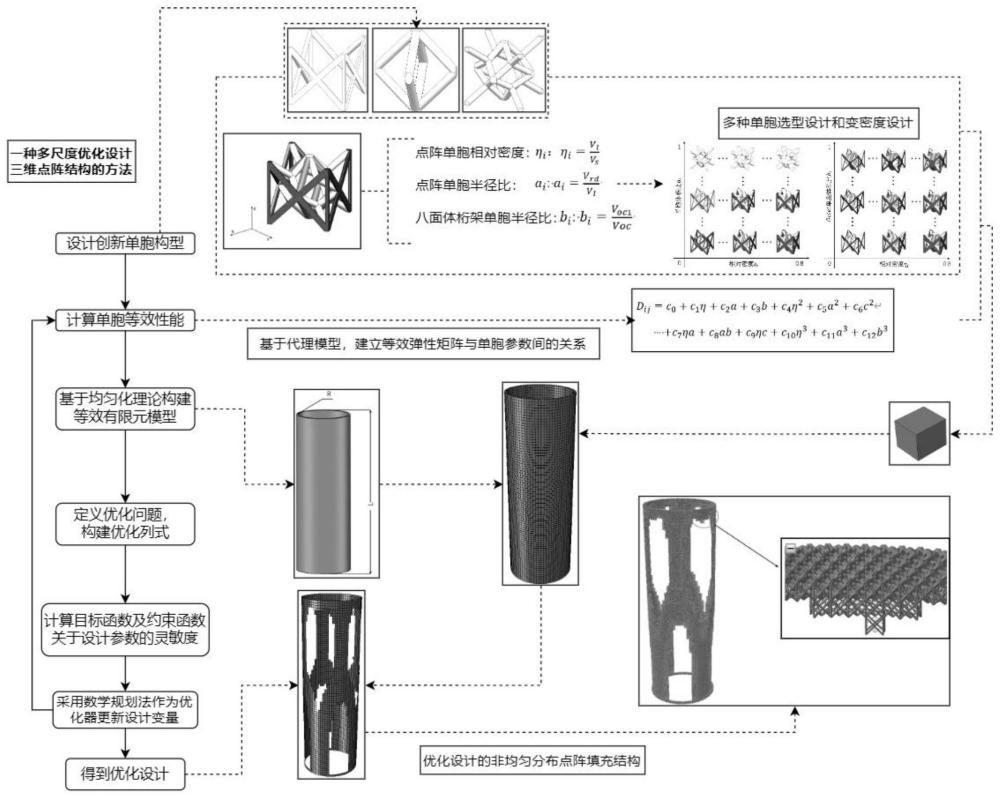
1、本发明针对上述实际工程中遇到的问题，发明了一种多尺度优化设计三维点阵结构的方法，三维点阵为具有非均匀点阵结构填充，该方法能同时优化设计宏观与微观两个尺度的结构。在微观尺度，点阵的尺寸与构型都有充足的设计空间。为了在减少计算成本的同时能保证计算精度，利用基于均匀化方法来获得点阵微观结构的等效性能，采用代理模型描述点阵单胞性能与设计参数的关系，进而在宏观尺度使用拓扑优化方法满足结构高性能与轻量化的需求，最终实现点阵填充结构的宏微观一体化优化设计。

2、本发明的技术方案如下：一种多尺度优化设计三维点阵结构的方法，步骤如下：

3、s1，采用两种单胞混合形成点阵单胞；所述点阵单胞基于菱形十二面体单胞、八面体桁架单胞的组合，保证节点位置连通性的情况下节点重合，通过建模直接组成点阵单胞；八面体桁架单胞包含外框架与内八面体，去除八面体桁架单胞内八面体中的水平支柱，并采用菱形十二面体单胞的支柱来弥补八面体桁架单胞x-y平面的力学性能；八面体桁架单胞外框架中的z向支柱加强点阵单胞z方向的承载能力；

4、s2，八面体桁架单胞外框架半径、八面体桁架单胞内八面体半径、菱形十二面体单胞支柱半径均为可变，点阵单胞组合形成点阵结构；

5、点阵单胞微观尺度的设计参数如下：

6、点阵单胞相对密度ηi：

7、点阵单胞半径比ai:

8、八面体桁架单胞半径比bi:

9、式中，vs是点阵单胞总体积，vl是点阵单胞支柱总体积，vrd是点阵单胞中菱形十二面体单胞支柱体积，voc是点阵单胞中八面体桁架单胞支柱体积，voc1是八面体桁架单胞内八面体中支柱体积；使用均匀化法对点阵单胞进行计算，得到其等效力学性能本构矩阵；

10、s3，采用代理模型建立等效力学性能本构矩阵与点阵单胞微观尺度的设计参数之间的关系；所述代理模型采取多项式拟合函数搭建表示为，

11、dij＝c0+c1η+c2a+c3b+c4η2+c5a2+c6c2+c7ηa+c8ab+c9ηc+c10η3+c11a3+c12b3  (4)

12、式中dij是均匀化计算得到的等效力学性能本构参数，ck是通过拟合不同设计参数所对应的均匀化数据的多项式系数，k＝1～12；

13、s4，将代理模型引入宏观结构拓扑优化中；根据均匀化理论，在宏观拓扑优化中将微观尺度的点阵单胞视为均质材料，根据代理模型计算得到分析中单元的材料属性，最终计算出单元刚度阵ki与整体刚度矩阵k；

14、s5，以最小化结构静态或动态柔顺度为目标的拓扑优化问题，计算目标函数：

15、

16、当仅考虑静态情况时候，目标函数可以表示为：c＝

17、

18、式中，c表示结构的总柔顺度，u是节点位移向量，f是外部载荷向量，ui是第i个单元的位移向量，ki是第i个单元的单元刚度矩阵；

19、目标函数分别对三个设计参数的灵敏度如下：

20、

21、

22、

23、其中，b是几何矩阵，是第i个单元的等效弹性系数矩阵，其导数通过直接求导得到；s6，设置拓扑优化的约束条件，包括结构体积约束与设计变量的变化范围约束，构建优化列式：

24、find:x＝{η1,…,ηn；a1,…,an；b1,…,bn}t

25、min:

26、s.t.:ku＝f

27、

28、0≤ηmin≤ηi≤ηmax≤1 i＝1,…,n

29、0≤amin≤ai≤amax≤1 i＝1,…,n

30、0≤bmin≤bi≤bmax≤1 i＝1,…,n

31、其中，vi为每一个单元的体积，vo为结构体积上限；ηmin、amin、bmin为设计变量的下限，ηmax、amax、bmax为设计变量的上限；

32、s7，采用数学规划法作为优化器更新设计变量；

33、s8，判断收敛条件：

34、||xnew-x||≤γ                         (11)

35、其中，γ为设定的收敛判别值，满足条件，迭代结束，不满足条件，返回步骤s3，继续迭代，直到满足收敛条件。

36、本发明的有益效果：

37、1)所设计的单胞充分考虑了可制造性因素，使得最终设计的点阵结构容易制造。

38、2)微观尺度点阵单胞采用了较少被研究的三维组合单胞，该单胞可同时改变构型与尺寸，设计空间大。

39、3)采用代理模型方法进行双尺度优化设计，使填充结构所用的点阵单胞可以是多构型的，同时可以做到计算成本较小的同时保证精度。