一种DBO-VMD-KELM的滚动轴承故障诊断方法

本发明涉及滚动轴承故障诊断，具体为一种dbo-vmd-kelm的滚动轴承故障诊断方法。

背景技术：

1、轴承作为机械设备的基本部件，其运行状态直接影响设备的性能、运行效率和使用寿命。利用其工作过程中产生的振动信号进行故障诊断，可以降低机械设备发生事故的概率，为设备后期维修计划提供可靠的决策支持，具有很高的实际意义。由于滚动轴承振动信号具有非平稳、非线性、易受多种因素影响的特点，这给故障信息的提取带来了困难，并且好的故障信息提取方法可以提高故障诊断模型中的准确度。故此好的信号提取方法和好的故障诊断方法是很重要的，不合适的参数设定对信号分解和诊断分类的结果都有显著影响，这些参数值的选择好坏直接影响到了诊断模型内的稳定性和诊断准确性，为了解决此影响，因此我们提出了一种dbo-vmd-kelm的滚动轴承故障诊断方法来解决上述问题。

技术实现思路

1、(一)解决的技术问题

2、针对现有技术的不足，本发明提供了一种dbo-vmd-kelm的滚动轴承故障诊断方法，解决了上述背景技术中所提出的问题。

3、(二)技术方案

4、本发明为了实现上述目的具体采用以下技术方案：

5、一种dbo-vmd-kelm的滚动轴承故障诊断方法，包括如下步骤：

6、步骤1：导入滚动轴承的振动信号数据；

7、步骤2：使用变分模态分解(vmd)对导入的振动数据进行信号分解，分解结果为内蕴模态函数(imf)分量；

8、步骤3：模态数(k)和惩罚因子(α)是变分模态分解中的两个重要的参数，该参数的选定对vmd的分解效果有直接的影响，选择蜣螂优化算法对这个关键参数组合[k,α],进行全局寻优，适应度函数采用最小包络熵函数；

9、步骤4：将寻优好的关键参数组合带回到vmd中，实现振动信号数据的最优信号分解；

10、步骤5：将最优分解后包络熵最小的内蕴模态函数(imf)分量作为最优imf分量，计算其时域上九个特征值，作为提取出来的特征向量；

11、步骤6：使用dbo算法对核极限学习机的核参数δ和正则化系数c进行优化；

12、步骤7：将特征向量送入到优化后的核极限学习机中故障诊断模型中师兄最终的故障诊断，并输出诊断结果。

13、进一步地，所述步骤1中导入的滚动轴承数据来源于由电机风扇端轴承的加速度传感器采集得到，振动信号总共分为五种类别，正常状态信号，内圈故障信号，滚动体故障信号和外圈故障信号。

14、进一步地，所述步骤2中使用变分模态分解(vmd)对导入的振动数据进行信号分解，其中vmd主要采用非递归技术，构建并求解一个有限变分问题，将复杂的初始信号解构为imf分量序列，具体步骤如下:

15、(2)构造约束变分表达式:

16、

17、

18、式(1.1)中:{uk}和wk分别表示模态分量和模态集合的频率中心；δ(t)和f(t)分别表示脉冲函数和原始信号，

19、(2)求解变分约束问题

20、式(1.2)中通过引入二次惩罚项(α)和拉格朗日乘子(λ)，将(1.1)的极值约束问题转化为无约束问题，推广的拉格朗日公式可以描述为：

21、

22、其中，a用于保证信号的重构精度，λ(t)为拉格朗日乘法算子，{uk}和{wk}分别表示第k个分量信号及其对应的中心频率，

23、vmd算法的过程如下:

24、步骤(1):启动迭代循环n＝n+1，

25、步骤(2):用公式(1.3)更新{uk(ω)}，

26、

27、步骤(3):更新中心频率{wk}，公式如下:

28、

29、步骤(4):将拉格朗日乘法算子{λ(ω)}更新为:

30、

31、步骤(5):重复步骤1-4，直至满足以下条件:

32、

33、进一步地，所述步骤3中，蜣螂算法(dbo)是一种元启发式算法，结合局部开发和全局搜索策略，在该算法中，蜣螂分为四种类型，即滚球、繁殖、觅食和偷窃，该算法通过这些行为寻找最优参数，并且抽象为数学语言，以下是每个行为的位置更新公式:

34、(1)滚动球行为

35、xi(t+1)＝xi(t)+α×k×xi(t-1)+b×δx,                 (1.7)

36、δx＝|xi(t)-xw|                          (1.8)

37、(2)繁殖行为

38、lb*＝max(x*×(1-r),lb),

39、ub*＝min(x*×(1+r),ub)                      (1.9)

40、xi(t+1)＝x*+b1×(xi(t)-lb*)+b2×(xi(t)-ub*)             (1.10)

41、(3)觅食行为

42、lbb＝max(xb×(1-r),lb),

43、ubb＝min(xb×(1+r),ub)                   (1.11)

44、xi(t+1)＝xi(t)+c1×(xi(t)-lbb)+c2×(xi(t)-ubb)           (1.12)

45、(4)偷窃行为

46、xi(t+1)＝xb+s×g×(|xi(t)-x*|+|xi(t)-xb|)        (1.13)

47、式中，t表示当前迭代次数，xi(t)表示屎壳郎的位置信息，δx模拟光照强度的变化，θ∈[0,π]，xw为全局最坏位置，xb为全局最优位置，

48、dbo-vmd的参数组合[k,α]寻优流程主要步骤如下，

49、(1)设置dbo的参数(种群数量、最大迭代次数、蜣螂类别比例、优化范围)，

50、(2)初始化种群，计算目标函数的适应度值，

51、(3)根据dbo的基本原则更新所有蜣螂的位置，

52、(4)确定每个目标是否超出边界，

53、(5)修正现有最优解及其适应度值，

54、(6)重复上述措施，直到满足终止准则，然后传递全局最优解[k,α]，

55、本文将蜣螂算法的种群为6:6:7:11的比例，将蜣螂划分为不同的角色，设置30个种群个体中有6个蜣螂用于滚球，6个蜣螂用于繁殖行为，7个蜣螂执行觅食行为，剩下的11个蜣螂被定义为小偷蜣螂用来执行偷窃行为，

56、包络熵可以分析某段信号的有序程度和反映信号中随机分量的数量，随机分量越多，包络熵越大，反之包络熵越小，基本思路是对希尔伯特变换后得到包络信号，结合信息熵，提取信号特征的过程，当信号利用希尔伯特解调后，会将原始信号序列转化成一个概率分布序列，而轴承发生故障时，产生的周期冲击也会使某段信号变得有序，包络熵变小，包络熵的计算公式为：

57、

58、

59、

60、上式中：ep为imf信号u的包络熵；m为imf信号长度；p为信号概率分布；a为imf信号u经希尔伯特解调得到的包络信号序列；h[]代表希尔伯特变换。

61、进一步地，所述步骤4中，将寻优好的关键参数组合带回到vmd中，实现对振动信号数据进行最优的信号分解。

62、进一步地，所述步骤5中，将最优分解后包络熵最小的内蕴模态函数(imf)分量作为最优imf分量，计算其时域上九个特征值，作为提取出来的特征向量，其中九个特征值分别为绝对平均值、峰峰值、标准差、均方根、峭度、峰值因子、脉冲因子、波形因子、裕度因子，数学表达式如下：

63、(1)绝对平均值

64、

65、(2)峰峰值

66、xmax-xmin(1.18)

67、(3)标准差

68、

69、(4)均方根

70、

71、(5)峭度

72、

73、(6)峰值因子

74、

75、(7)脉冲因子

76、

77、(8)波形因子

78、

79、(9)裕度因子

80、

81、进一步地，所述步骤6中使用db0算法对核极限学习机的核参数δ和正则化系数c进行优化，具体优化流程如下：

82、(1)设置dbo的参数(种群数量、最大迭代次数、蜣螂类别比例、优化范围)；

83、(2)初始化种群，计算目标函数的适应度值；

84、(3)根据dbo的基本原则更新所有蜣螂的位置；

85、(4)确定每个目标是否超出边界；

86、(5)修正现有最优解及其适应度值；

87、(6)重复上述措施，直到满足终止准则，然后传递全局最优解，参数δ和正则化系数c。

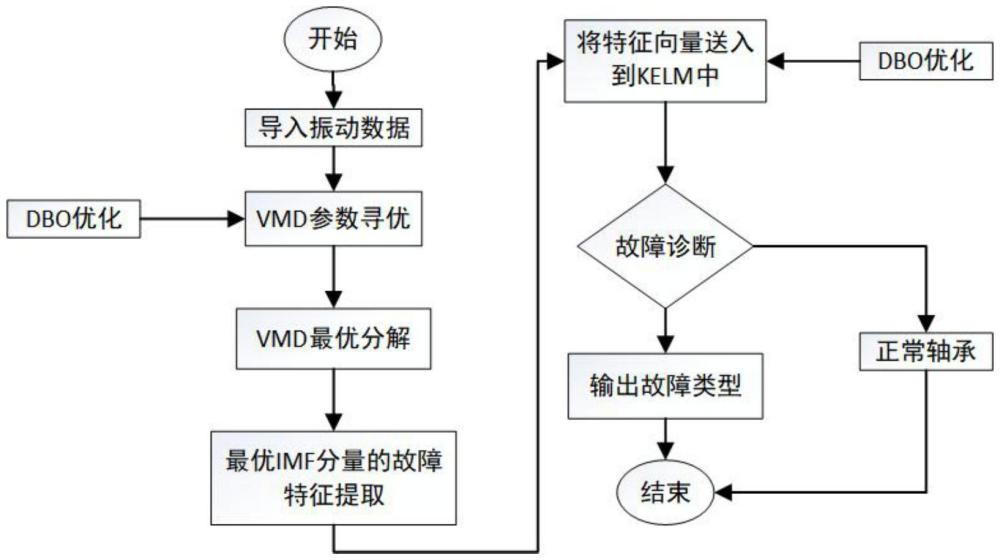
88、进一步，所述步骤7中，将提取出来的特征向量送入到优化后的核极限学习机中故障诊断模型中实现最终的故障诊断，并输出诊断结果；dbo-vmd-kelm模型的整个诊断流程如下：

89、步骤(1)：导入预处理后的滚动轴承振动信号数据；

90、步骤(2)：使用蜣螂优化算法对vmd算法进行优化，以包络谱熵作为适应度函数，对模态个数k和惩罚因子α进行全局寻优；

91、步骤(3)：将优化后的最佳参数组合带回到vmd模型中，以对导入的数据进行信号分解，并得到其本征模态分量；

92、步骤(4)：选取包络熵最小的本征模态分量作为其最优分量，并计算其时域特征；本文选取其九个时域特征值进行计算，分别为绝对平均值、峰峰值、标准差、均方根、峭度、峰值因子、脉冲因子、波形因子、裕度因子；

93、步骤(5)：使用蜣螂优化算法对kelm算法的关键参数进行全局寻优；

94、步骤(6)：将计算好地九个指标作为特征向量，送入到kelm诊断模型中进行训练，并输出故障诊断结果。

95、(三)有益效果

96、与现有技术相比，本发明提供了一种dbo-vmd-kelm的滚动轴承故障诊断方法，具备以下有益效果：

97、本发明，通过使用变分模态分解作为故障诊断模型中的信号分解方法，相对于一些常用的信号处理方法，如小波变换、经验模态分解(emd)，局部模态分解(lmd)等，这些方法都存在模态混叠等缺陷，而变分模态分解(vmd)由于具有良好的噪声鲁棒性和有效抑制模态混叠和端点效应的能力，可以更好的对故障信息进行提取。

98、本发明，变分模态分解(vmd)的参数组合[k,α]，对分解效果有显著影响，不合适的模态数k会导致过分解或欠分解，惩罚因子α通过改变带宽直接影响分解精度。因此，本文采用蜣螂优化算法对变分模态分解的关键参数进行全局寻优，可以有效确定最优参数组合。

99、本发明，极限学习机相比于常见机器学习算法具有学习效率高和泛化性能的优势。而本文选择核极限学习机(kelm)作为故障诊断模型，该方法不仅具有极限学习机的优点，还进一步的提高了分类精度，并且具有更强的鲁棒性，然而kelm的分类精度对核参数δ和正则化系数c的设置很敏感。本文同样采用蜣螂优化算法对核极限学习机的关键参数进行全局寻优。