一种海洋结构物疲劳损伤演化模型参数计算方法

本发明涉及海洋结构物疲劳损伤预测，尤其涉及一种海洋结构物疲劳损伤演化模型参数计算方法。

背景技术：

1、海洋结构物在其服役年限内，既会受到来自风、浪、流等长期循环载荷作用，也可能会受到台风、地震等短期极端循环载荷的作用，结构弹性和塑性损伤相互叠加、相互耦合，将不可避免的引起海洋结构物疲劳损伤，甚至断裂破坏。

2、耦合损伤的弹塑性本构模型、弹性损伤演化模型和塑性损伤演化模型可有效的预测海洋结构物的疲劳损伤。金属板材是海洋结构物中的常见组成，因此在通过耦合损伤的弹塑性本构模型、弹性损伤演化模型和塑性损伤演化模型预测海洋结构物的疲劳损伤时，需要对金属板材的模型参数进行求解。

3、然而，耦合损伤的弹塑性本构模型、弹性损伤演化模型和塑性损伤演化模型的参数众多、类别复杂和求解困难的问题。

4、上述内容仅用于辅助理解本发明的技术方案，并不代表承认上述内容是现有技术。

5、鉴于此，特提出此发明。

技术实现思路

1、本发明的目的是为了解决现有技术中存在的缺点，而提出的一种海洋结构物疲劳损伤演化模型参数计算方法，用于求解海洋结构物中金属板材的模型参数。

2、为了实现上述目的，本发明采用了如下技术方案：

3、一种海洋结构物疲劳损伤演化模型参数计算方法，包括如下步骤：

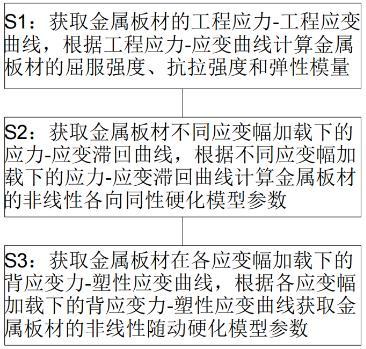
4、s1：获取金属板材的工程应力-工程应变曲线，根据工程应力-应变曲线计算金属板材的屈服强度、抗拉强度和弹性模量；

5、s2：获取金属板材不同应变幅加载下的应力-应变滞回曲线，根据不同应变幅加载下的应力-应变滞回曲线计算金属板材的非线性各向同性硬化模型参数；

6、s3：获取金属板材在各应变幅加载下的背应变力-塑性应变曲线，根据各应变幅加载下的背应变力-塑性应变曲线获取金属板材的非线性随动硬化模型参数。

7、进一步，所述s1包括如下步骤：

8、s11：通过单调拉伸试验获取金属板材的荷载-工程应变曲线；

9、s12：根据金属板材的荷载-应变曲线以及如下公式计算工程应力，

10、，

11、公式中，f为荷载，从荷载-工程应变曲线获取，为板材平行中段的初始横截面积；

12、s13：构建金属板材的工程应力-工程应变曲线，根据工程应力-工程应变曲线获取金属板材的屈服强度、抗拉强度和弹性模量。

13、进一步，所述s2包括如下步骤：

14、s21：通过低周疲劳循环加载试验获取金属板材不同应变幅加载下的应力-应变滞回曲线；

15、s22：根据如下公式计算累积塑性应变值和各向同性应力值，

16、，

17、，

18、公式中，为循环加载周期，为塑性应变幅值，从应力-应变滞回曲线获取，、分别为滞回曲线中弹性区域的应力上限和下限，从应力-应变滞回曲线获取；

19、s23：拟合函数拟合曲线，并根据曲线和如下公式计算金属板材的非线性各向同性硬化模型参数，将平均值作为金属板材的非线性各向同性硬化模型参数，

20、，

21、公式中，为累积塑性应变的应力，为材料屈服面产生塑性变形后所能达到的最大变化范围，为表征屈服面随累积塑性应变增加而变化的速率。可根据应变比的单轴循环载荷下的试验数据拟合曲线获取参数、和。

22、进一步，所述s3包括如下步骤：

23、s31：通过低周疲劳循环加载试验获取金属板材各应变幅加载下在半寿命周期处=158、280、510、1100、2150的稳定滞回曲线；

24、s32：根据金属板材的应力-应变曲线、应力-塑性应变曲线和背应力-塑性应变曲线，将金属板材各应变幅加载下在半寿命周期处=158、280、510、1100、2150的稳定滞回曲线分解为金属板材在各应变幅加载下的背应力-塑性应变曲线；

25、s33：根据金属板材在各应变幅加载下的背应力-塑性应变曲线获取各应变幅下的单级背应力系数、，并将各应变幅下的单级背应力系数、的平均值作为金属板材的单级背应力系数、；

26、s34：金属板材的单级背应力系数、分解为三级背应力系数三级背应力系数、()。

27、进一步，还包括：

28、s4：获取金属板材的s-n曲线和曲线，根据金属板材的s-n曲线和曲线获取金属板材弹性疲劳损伤模型参数。

29、进一步，所述s4包括如下步骤：

30、s41：获取金属板材在平均应力，应力比下的s-n曲线，将金属材料弹性疲劳损伤演化模型以对数坐标系表示，采用最小二乘法回归拟合金属板材弹性疲劳损伤模型参数、；

31、s42：获取金属板材的材料参数a，并计算；

32、s43：获取金属板材在平均应力循环对称加载下的曲线，并根据平均应力循环对称加载下的曲线获取金属板材弹性疲劳损伤模型参数和。

33、进一步，还包括：

34、s5：获取金属板材在不同应变幅值下，半寿命周期处稳定滞回曲线的塑性应变幅、最大应力幅值、弹性应变幅，根据不同应变幅值下，半寿命周期处稳定滞回曲线的塑性应变幅、最大应力幅值、弹性应变幅获取金属板材的塑性疲劳损伤参数。

35、进一步，所述s5包括如下步骤：

36、s51：通过应变比的应变幅加载下的低周循环疲劳试验，获取金属板材在不同应变幅值下，半寿命周期处稳定滞回曲线的塑性应变幅、最大应力幅值、弹性应变幅；

37、s52：结合manson-coffin模型式与不同应变幅加载下的塑性应变及疲劳寿命试验结果，构造曲线，采用幂函数法拟合参数疲劳塑性系数、疲劳塑性指数；

38、s53：结合ramberg-osgood模型与不同应变幅值下，半寿命周期处稳定滞回曲线的塑性应变幅、最大应力幅值、弹性应变幅构造曲线，采用幂函数拟合曲线获取塑性疲劳损伤参数、；

39、s54：通过对数坐标系下金属板材的塑性疲劳演化模型拟合疲劳寿命-塑性应变曲线，结合、拟合值线性回归获取塑性疲劳损伤参数、。

40、本发明与现有技术相比，其有益效果为：

41、1、给出了疲劳损伤演化模型中弹塑性本构模型和弹塑性统一疲劳损伤演化理论模型的系统性参数求解方法，该方法解决了疲劳损伤模型参数众多，类别复杂，求解困难的问题。并以ah36钢为例，完整的对其疲劳损伤演化模型参数进行了求解，详细的展示了其每一个参数所需的试验数据及拟合方法。随后，将ah36钢参数运用到了有限元仿真中进行应力应变力学响应分析，通过对比试验和仿真的单调应力应变曲线和应力应变前10圈滞回曲线，验证了试验所标定的参数及求解过程的准确性。因此，本实施例的方法能有效为疲劳损伤演化模型数值分析运用提供技术支撑。

42、2、通过开展单调拉伸试验、s-n曲线法及板材低周疲劳循环加载试验进行本构模型参数的拟合，可以更好的对金属板材塑性运动状态进行表征；进行弹塑性统一疲劳损伤演化理论模型的拟合，可以更好的模拟金属板材的损伤演化过程。

43、3、可以系统的拟合不同金属板材的疲劳损伤演化模型参数，可用于开展结构损伤数值仿真分析，实现连续损伤力学在结构疲劳裂纹萌生及扩展中的运用。

44、4、分别对其材料参数屈服强度、抗拉强度、弹性模量，表征塑性的非线性混合强化模型参数、、、，弹性疲劳损伤演化模型参数、、、及塑性疲劳损伤演化模型参数、、、、、进行表征求解。该方法为疲劳损伤演化模型的数值仿真应用提供了强有力的数据支撑。