一种基于水资源适应性管理的河流生态系统保护方法

本技术涉及自然生态系统保护管理领域，尤其是涉及一种基于水资源适应性管理的河流生态系统保护方法。

背景技术：

1、水资源是河流生态系统的核心，其合理配置在河流生态系统保护中至关重要。水资源的有限性决定了其通常无法同时满足经济社会发展及生态保护的不同需求，因此水质保护与水资源利用主体间存在博弈权衡。一方面，经济发展与城镇化进程加快导致需水量及社会经济用水效益增加；另一方面，经济社会用水后的污水排放量对水生态环境施加压力负荷，带来水质恶化、水环境容量降低等一系列问题。基于此如何协调水质保护与水资源利用关系，实现河流生态系统保护及经济高质量发展成为亟待解决的问题。

2、水资源优化配置是解决水资源问题、实现水资源可持续利用的有效手段。目前针对水质保护与水资源利用的优化决策，大多聚焦于确定情况下的优化配置，往往将模型参数简化处理成确定性数值，决策结果易产生偏差。随着气候变化影响加剧和水资源系统不确定性增大，迫切需要水资源适应性管理方法，以处理水资源系统中的不确定性，提高应对系统风险和不确定性的能力。

技术实现思路

1、针对现有技术中存在的上述问题，本技术提供一种基于水资源适应性管理的河流生态系统保护方法。

2、本技术提供的一种基于水资源适应性管理的河流生态系统保护方法采用如下的技术方案：

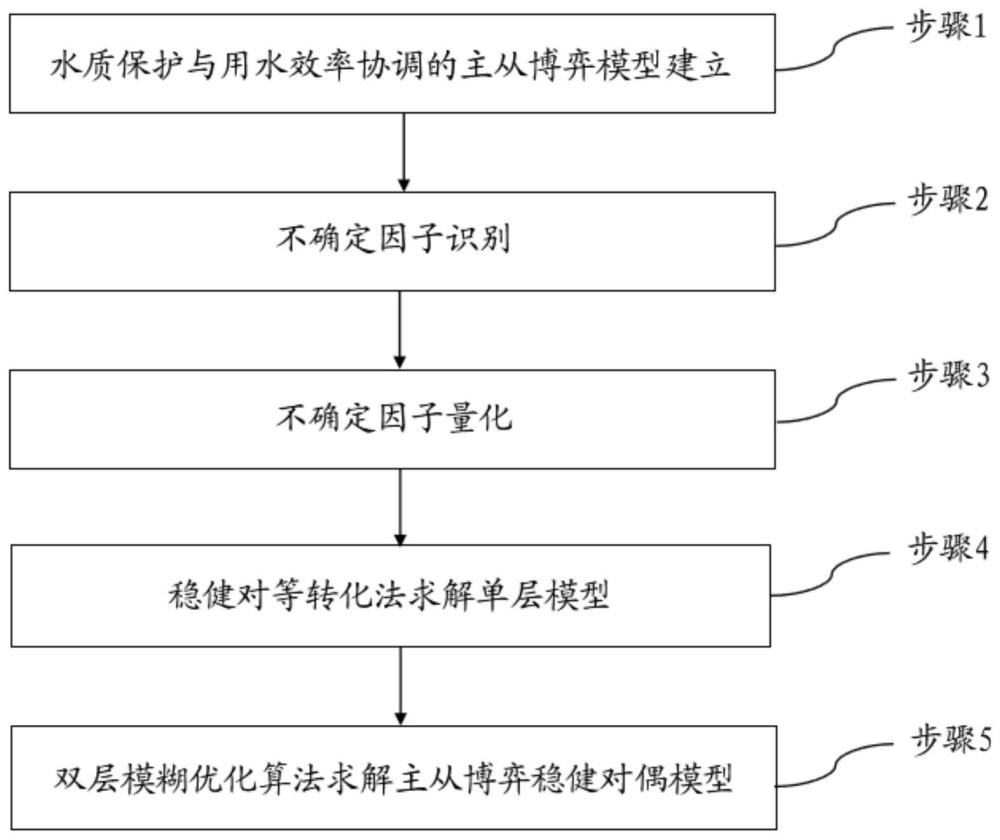
3、一种基于水资源适应性管理的河流生态系统保护方法，包括以下步骤：

4、步骤1、建立水质保护与用水效率协调的主从博弈模型；

5、步骤2、识别所述水质保护与用水效率协调的主从博弈模型中的不确定因子，包括输入数据及模型参数，输入数据为各水资源分区各用水部门的需水量及研究区总可供水量，模型参数为各水资源分区各用水部门的排污参数及用水效益参数；

6、步骤3、量化所述不确定因子，构建随机需水量、随机可供水量、随机排污参数及随机用水效益参数的区间不确定集；

7、步骤4、应用稳健优化得到水质保护与用水效率协调的主从博弈稳健优化模型；基于对偶理论进行对偶转换，将水质保护与用水效率协调的主从博弈稳健优化模型转化为易于求解的线性形式，得到水质保护与用水效率协调的主从博弈稳健对偶模型；

8、步骤5、采用双层模糊优化法求解所述水质保护与用水效率协调的主从博弈稳健对偶模型，得到水质保护与用水效率协调的适应性最优解，实现对不确定环境下水资源的优化配置。

9、进一步地，所述步骤1中，水质保护与用水效率协调的主从博弈模型以水质保护主体为上层领导者，目标函数为排污总量最小，以水资源利用主体为下层跟从者，目标函数为经济效益最大，以可供水量约束、需水量约束及非负约束作为约束条件。

10、进一步地，所述步骤1中，水质保护与用水效率协调的主从博弈模型表达式为：

11、

12、公式(1)中，fu(x)为上层水质保护主体的排污总量；fl(x)为下层水资源经济利用主体的经济效益；i表示资源分区编号，m为资源分区总数，j为用水部门编号，n为用水部门总数；cj、nj、pj、hj分别为第j个用水部门排放cod、tn、tp和nh3-n的浓度；为第j个用水部门的随机排污系数；为第i个水资源分区的第j个用水部门的随机用水效益系数；为研究区域的随机可供水量；为第i个水资源分区的第j个用水部门的随机需水量；α为研究区域刚性需水比例；xij为决策变量，代表第i个水资源分区的第j个用水部门所分配到的水量，为表示任意的符号。

13、进一步地，所述步骤3中，随机参数需水量、可供水量、排污参数及用水效益参数的区间不确定集表示如下：

14、

15、

16、

17、

18、公式(2)-(5)中，为第i个水资源分区的第j个用水部门的需水量基值，取该水资源分区该用水部门多年需水量均值；εd为需水量的不确定度，ηdij为第i个水资源分区的第j个用水部门随机需水量波动的标度偏差，表示随机需水量偏离需水量基值的程度；γd为需水量的保护水平，表示允许随机需水量波动的阈值；为研究区域的可供水量，为第i个水资源分区的第j个用水部门的用水效益系数，为第j个用水部门的排污系数基值；εaw、εner、εe分别为可供水量、用水效益参数、排污参数的不确定度；ηaw、ηnerij、ηej分别为可供水量、用水效益参数、排污参数波动的标度偏差，γaw、γner、γe分别为可供水量、用水效益参数、排污参数的保护水平。

19、进一步地，所述步骤4包括：

20、步骤4.1、基于稳健对等转换法为水质保护与用水效率协调的主从博弈模型引入不确定参数，构建上层水质保护稳健优化模型和下层水资源利用稳健优化模型的稳健形式；

21、步骤4.2、基于对偶理论求解上层排污总量目标和下层经济效益目标，引入强对偶参数，得到水质保护与用水效率协调的主从博弈稳健对偶模型。

22、进一步地，所述步骤4.1中，针对不确定排污参数，上层排污总量目标的稳健对等形式表示如下：

23、

24、针对不确定用水效益参数，下层经济效益目标的稳健对等形式表示如下：

25、

26、针对不确定需水量参数和不确定可供水量参数，需水量约束、可供水量约束的稳健对等形式如下：

27、

28、

29、进一步地，所述步骤4.2中，上层水质保护主体的稳健对偶形式表示如下：

30、

31、下层水资源利用主体的稳健对偶形式表示如下：

32、

33、其中，c1-c4为公式(6)、(8)、(9)的对偶形式，c5-c8为公式(7)、(8)、(9)的对偶形式，z1-z8、p1-p8为稳健公式的对偶变换引入的辅助参数。

34、进一步地，所述步骤5包括：

35、步骤5.1、将上层领导者与下层跟从者的目标函数描述为隶属度函数，以反映上层目标与下层目标的满意度；

36、步骤5.2、引入上层决策变量范围的隶属度函数，允许下层跟从者在该容许范围内寻找最优解。

37、进一步地，所述步骤5.1中，上层领导者水质保护模型目标函数的隶属度函数为：

38、

39、其中，为上层水质保护模型目标函数的隶属度函数；为上层目标函数单独求解时的最小值；为下层目标函数单独求解时的最优解；为下层最优解代入上层目标函数所得到的值；

40、下层跟从者水资源利用模型目标函数的隶属度函数为：

41、

42、其中，为下层水资源利用模型目标函数的隶属度函数；为下层目标函数单独求解时的最优值；为上层目标函数单独求解时的最优解；为上层最优解代入下层目标函数所得到的值。

43、进一步地，所述步骤5.2包括：

44、步骤5.2.1、在上层领导者与下层跟从者的交互过程中，上层领导者给下层跟从者一个可接受的决策变量范围，引入容忍度置信水平α，求得上层决策范围的置信水平为α时新的可行域空间集上层决策变量的隶属度函数的公式如下：

45、

46、其中，为上层决策变量的隶属度函数，为上层目标函数单独求解时的最大值；

47、步骤5.2.2、上层领导者与下层跟从者的满意度用隶属度表示，若达到上层和下层决策问题的满意程度，则得到最终结果；否则，上层决策问题会向下层决策问题提供新的隶属度函数作为控制变量和目标，直至得到主从博弈模型最优解，求解公式如下：

48、

49、其中，λ、λu、λl分别为求解主从博弈模型的整体满意度、上层领导者的满意度、下层跟从者的满意度；λu1为上层领导者可接受的目标函数最小隶属度；β为上层领导者可接受的决策变量最小隶属度。

50、综上所述，本技术提供的方法能够有效实现河流生态系统保护，基于主从博弈稳健优化方法，应对河流生态系统中水资源的不确定性，控制经济用水产生的排污总量，协调水环境保护与经济发展关系，为水生态管理者提供稳健适应性管理方法。