基于改进符号动力学熵的旋转机械故障诊断方法

本发明属于故障诊断,涉及一种旋转机械故障诊断方法，具体涉及一种基于改进符号动力学熵的旋转机械故障诊断方法。

背景技术：

1、作为广泛应用的机械零部件，滚动轴承、齿轮、转子等旋转机械在恶劣的环境下工作易导致其出现各种故障。故障的发生会带来巨大的损失，甚至威胁到生命安全。因此对其进行故障诊断意义重大。滚动轴承故障信号特征微弱，传统的基于线性系统的时域和时频域信号分析方法很难准确地提取轴承的故障特征信息。随着非线性动力学的发展，出现了一些非线性动力学分析技术，为分析旋转机械复杂的非线性动力学行为提供了一种很好的选择。这其中近似熵、样本熵、多尺度熵和符号动力学熵等都被引入到旋转机械的故障诊断中，并取得了很好的诊断效果。

2、但是这些基于熵算法的特征提取方法本身也存在一些问题，如:近似熵的相似性差；样本熵虽相比其它非线性参数具有一定的优势，但其易受时间序列中的异常值影响，稳定性差；排列熵(permutation entropy,pe)能反映信号的随机性和动态突变性,但仅在提取序数模式时保留序数结构，若仅提取顺序结构，易丢失幅值信息。

3、cn2010105647486公开一种汽轮发电机组低频振动与功率递增相关性分析方法。包括每隔第一步进长度,采集并存储当前时刻机组功率数据；每隔第二步进长度,计算当前时刻低频振动幅值熵并存储；计算机组功率数据序列的递增趋势参数；计算低频振动幅值熵序列的递增趋势参数以及低频振动幅值熵序列的变化偏度参数；判断机组功率递增趋势实时验证与低频振动幅值熵突变性实时验证是否都通过。实现机组功率递增与低频振动增强的相关性自动实时在线监测和判别。

4、cn2020101655133基于信息熵的旋转机械振动故障诊断方法及其系统，基于信息熵的旋转机械振动故障诊断方法包括如下步骤：获取旋转机械的振动数据；利用振动数据构建多维时间序列矩阵，并对该多维时间序列矩阵进行处理从而获得时域信号矩阵；对时域信号矩阵中的每个元素进行处理，得到幅值谱矩阵和功率谱矩阵；对各类矩阵中的每一个序列进行信息熵计算，并通过信息熵的值反映旋转机械的状态；其中，各类矩阵包括：时域信号矩阵、幅值谱矩阵和功率谱矩阵；各类矩阵中的每个元素均为一个序列。本技术具有给出设备的故障特征而且能对其进行量化估计，实现机械故障在定性和定量两方面判断。

技术实现思路

1、本发明目的在于，针对现有旋转机械振动信号的故障诊断方法尚存在噪声背景下特征提取可分性不强、故障识别准确率低及故障严重程度分析不充分等问题，提出一种基于改进多尺度符号动力学熵的旋转机械故障诊断方法。

2、本发明的技术方案是：一种基于改进改进符号动力学熵的旋转机械故障诊断方法，包括如下步骤：

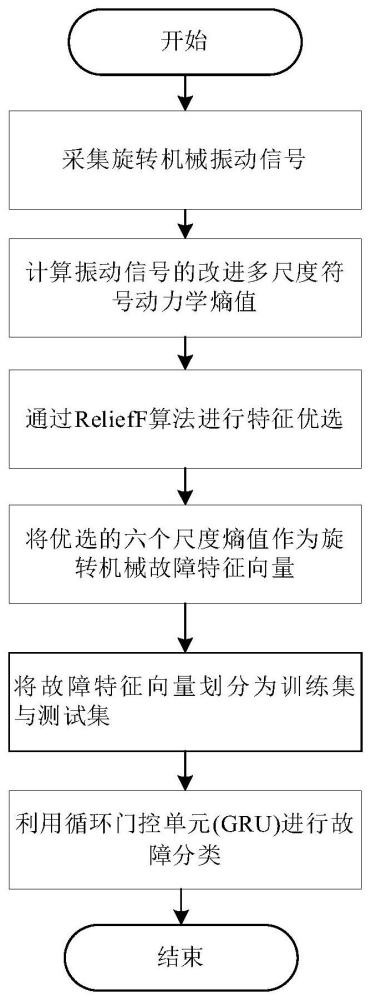
3、步骤1：获取不同故障类型、不同噪声背景下的旋转机械振动信号，将每类振动信号划分为100个样本，每个样本2048个数据点；

4、步骤2：计算所有样本的改进多尺度符号动力学熵；

5、步骤3：通过relieff算法进行特征优选，选择权值最高的前六个尺度上的改进符号动力学熵作为故障特征向量；

6、步骤4：将故障特征向量划分为训练集与测试集。

7、步骤5：通过深度学习网络门控循环单元(gru)进行故障分类与诊断。

8、步骤2中：计算所有样本的改进多尺度符号动力学熵，包括：

9、步骤2-1：对一个时间序列{xi}＝{x1,x2,…,xn}，通过z分数法进行异常值检测并以序列中位数替换异常值点，将z分数的绝对值大于3的数据点视为异常值；得到新的时间序列计为{xi'}＝{x′1,x'2,…,x'n}。

10、其中，z分数计算公式：

11、

12、其中，xi为时间序列的值，μ为均值，σ表示标准差。

13、步骤2-2：通过均值标准差归一化多尺度方式对剔除异常点的时间序列{x′i}进行粗粒化处理。

14、步骤2-3：符号化时间序列。将时间序列根据其数值的大小分为不同的个ε数值区间，用符号σi(i＝1,2,…,ε)来替代原始时间序列的每一个元素，从而把原始时间序列重构成符号序列z{z(k),k＝1,2,…,n}；

15、步骤2-4：根据符号序列构建子向量，计算重构序列的状态模式概率建立状态模式矩阵。给定嵌入维数m和时间延迟λ，可以将重构后的符号序列z{z(k),k＝1,2,…,n}拆分成不同的子序列：

16、

17、每个子序列的符号状态模式都是唯一的，每个子序列包含m个元素，其中每一个元素的符号选择空间有ε种，因此这些重构的子序列总共有εm种不同的符号排列状态模式。定义为每个子序列符号排列的状态模式，则其在全部子序列中出现的概率如下：

18、

19、其中，type(·)为符号序列与状态模式之间的映射关系，||·||表示集合中元素的数目。

20、在此基础上构建状态模式矩阵

21、步骤2-5：计算改进的状态迁移概率并构建状态迁移矩阵。计算得到状态模式后，之后出现的符号为σb(b＝1,2,…ε)的概率为状态迁移概率：

22、

23、其中状态迁移概率满足

24、在此基础上构建的εm×ε的状态模式矩阵形式如下：

25、步骤2-6：计算所有尺度下的改进多尺度符号动力学熵。

26、

27、其中，isde为采用步骤2-5中方法改进的sde。

28、步骤3：通过relieff算法进行特征优选，选择权值最高的前六个尺度上的改进符号动力学熵作为故障特征向量，具体包括：

29、步骤3-1：给定样本集k和特征集f。并初始化迭代次数l与选取的临近样本个数k；

30、步骤3-2：从样本集中随机选取样本r，从与r同类样本中选取k个近邻点记为hj，从与r不同类样本中选取k个近邻点记为mj(c)。重复执行以上操作l次；

31、步骤3-3：计算重要度权值w(a)。

32、

33、其中，a为故障特征，diff(a,r,hj)表示r与hj在a下的距离，w(a)值越大，说明a对样本的区分能力越强。

34、步骤3-4：重复步骤3-3n次，输出重要度向量w，则a对应的特征权值为

35、

36、其中n为特征个数。

37、有益效果：相对于现有技术，本发明的优点包括：本发明基于z分数法进行时间序列的异常值检测，消除异常数据的影响；通过一种均值标准差归一化的粗粒化方法解决传统粗粒化方法带来的熵值偏差缺陷；引入动态调整方法，根据时间序列中的当前位置和最大嵌入维数来改进状态模式概率，更好地捕捉序列的依赖关系。通过改进的符号动力学熵，能够提取更加丰富的轴承状态信息，在故障模式识别过程中有更高的识别率。本发明采用均值标准差归一化方法代替的传统多尺度方法，通过动态调整的方式更新状态模式概率，计算不同尺度下的改进符号动力学熵。改进后的多尺度符号动力学熵能更全面地反映信号的特征，具有更强的抗噪能力，从而更准确地评估旋转机械的运行状态。本发可以广泛应用于旋转机械故障诊断领域。