一种基于不对称信息流的数据间因果结构发现方法

本发明涉及因果诊断，具体是一种基于不对称信息流的数据间因果结构发现方法。

背景技术：

1、因果结构生成领域目前的发展十分迅速，热门研究都是基于约束方法，这类方法的好处在于适用性比较广泛，但是处理数据比较复杂，并且都是基于非时序数据集；同时需要比较充分的假设，容易包含错误的边和方向，处理后生成的是markov等价类。

2、在对变量x2进行干预后，变量x1与变量x2相互独立，因此无法确定唯一的因果骨架图，此时就会用到基于函数因果模型的方法，该方法是基于约束方法的改进。目前比较热门的函数因果模型包括：ligan模型、anm（加性噪声模型）、pnl等等。尽管上述这些模型能够处理因果关系，但是他们需要满足特定的条件。比如lingan模型中引用的数据必须是线性非高斯无环类数据，而anm模型必须满足加性噪声场景等等。同时现在基于时序观察数据的因果发现存在较多的研究空白。比较典型的方法有转移熵和格兰杰因果发现，但是格兰杰因果发现方法存在未观测到的变量、时间分辨率低，以及观测噪声等问题，这些问题会导致出现虚假的格兰杰因果关系。转移熵定理因果发现有时候无法恢复许多预设的单向因果关系，也有可能给出错误的方向。同时，在发生故障的过程中观察到的数据往往是非线性与非平稳性，传统的因果发现方法适用性不够，导致生成的因果关系准确度降低，因此亟待解决。

技术实现思路

1、为了避免和克服现有技术中存在的技术问题，本发明提供了一种基于不对称信息流的数据间因果结构发现方法。本发明能够有效地提高因果图生成的准确性。

2、为实现上述目的，本发明提供如下技术方案：

3、一种基于不对称信息流的数据间因果结构发现方法，包括以下生成步骤：

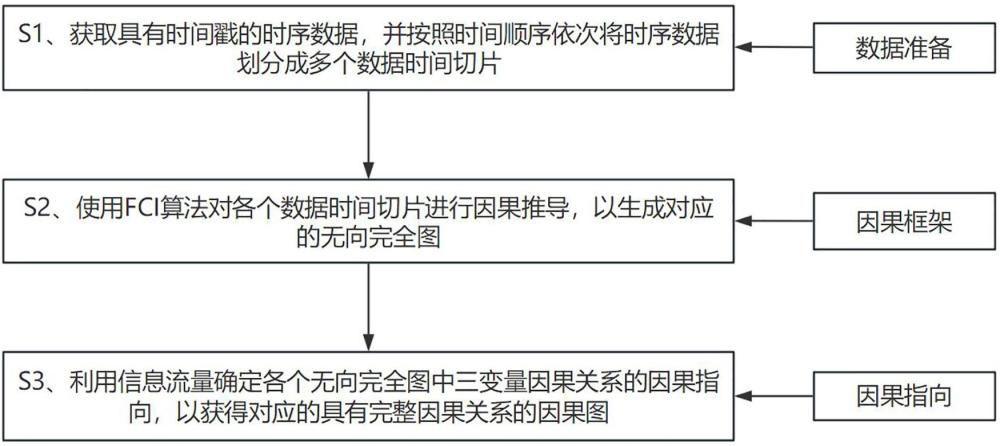
4、s1、获取具有时间戳的时序数据，并按照时间顺序依次将时序数据划分成多个数据时间切片；

5、s2、使用fci算法对各个数据时间切片进行因果推导，以生成对应的无向完全图；

6、s3、利用信息流量确定各个无向完全图中三变量因果关系的因果指向，以获得对应的具有完整因果关系的因果图。

7、作为本发明的进一步技术方案：利用信息流量确定三变量因果关系的因果指向的具体步骤如下：

8、s31、从当前时间段对应的无向完全图中任选一个变量x2；并以该变量x2为中心变量，从无向完全图中选取两个与该中心变量相邻的变量x1和变量x3作为相邻变量；中心变量和两个相邻变量共同构成三变量因果项(x1,x2,x3)；

9、s32、通过对应的计算公式计算三变量因果项(x1,x2,x3)中的各个变量的信息熵变化率，以及对应的边际熵变化率；

10、s33、根据计算出的信息熵变化率和边际熵变化率，计算三变量因果项(x1,x2,x3)中的各个变量之间的信息流量；

11、s34、基于计算出的信息流量，根据因果指向判断准则，判断三变量因果项(x1,x2,x3)中各个变量之间的因果指向；

12、s35、按照步骤s31到步骤s34的内容确定当前无向完全图中所有三变量节点项的因果指向，以将当前的无向完全图转化成因果关系明确的祖先图；

13、s36、根据时间顺序，按照步骤s35的内容将总时间t内的各个无向完全图均转化成对应的祖先图。

14、作为本发明的再进一步技术方案：变量x1的信息熵变化率的计算公式如下：

15、；

16、式中，表示在当前时间段(ti,ti+δt)内，处于ti+δt时刻时，变量x1的信息熵，δt表示时间间隔，ti表示第i个时刻；表示随时间的变化率，即变量x1的信息熵变化率；e表示期望；f1表示变量x1随时间变化的输入函数；表示在当前时间段(ti,ti+δt)内，处于ti+δt时刻时，变量x1的边际概率密度函数；表示多元求导符号；g111表示一阶矩阵参数；log表示指数函数；

17、变量x2的信息熵变化率包括变量x2的第一信息熵变化率和变量x2的第二信息熵变化率；

18、变量x2的第一信息熵变化率的计算公式如下：

19、；

20、式中，表示在当前时间段(ti,ti+δt)内，处于ti+δt时刻时，变量x2的第一信息熵；表示随时间的变化率，即变量x2的第一信息熵变化率；f2表示变量x2随时间变化的输入函数；表示在当前时间段(ti,ti+δt)内，处于ti+δt时刻时，变量x2的边际概率密度函数；g122表示第一二阶矩阵参数；

21、变量x2的第二信息熵变化率的计算公式如下：

22、；

23、式中，表示在当前时间段(ti,ti+δt)内，处于ti+δt时刻时，变量x2的第二信息熵；表示随时间的变化率，即变量x2的第二信息熵变化率；g222表示第二二阶矩阵参数；

24、变量x3的信息熵变化率包括变量x3的第一信息熵变化率和变量x3的第二信息熵变化率；

25、变量x3的第一信息熵变化率的计算公式如下：

26、；

27、式中，表示在当前时间段(ti,ti+δt)内，处于ti+δt时刻时，变量x3的第一信息熵；表示随时间的变化率，即变量x3的第一信息熵变化率；f3表示变量x3随时间变化的输入函数；表示在当前时间段(ti,ti+δt)内，处于ti+δt时刻时，变量x3的边际概率密度函数；g133表示第一三阶矩阵参数；

28、变量x3的第二信息熵变化率的计算公式如下：

29、；

30、式中，表示在当前时间段(ti,ti+δt)内，处于ti+δt时刻时，变量x3的第二信息熵 ；表示的变化率，即变量x3的第二信息熵变化率；g233表示第二三阶矩阵参数。

31、作为本发明的再进一步技术方案：变量的边际熵变化率的计算公式如下：

32、；

33、式中，表示在当前时间段(ti,ti+δt)内，处于ti+δt时刻时，在排除变量x2对变量x1影响的情况下，其他变量对变量x1产生影响时的边际熵；表示随时间的变化率，即变量x1的边际熵变化率；表示在当前时间段(ti,ti+δt)内，处于ti+δt时刻时，在排除变量x2对变量x1影响的情况下，变量x1的边际概率密度函数；dx3表示变量x3的微分；dxn表示变量xn的微分，n表示变量的总类别数；

34、变量x2的边际熵变化率包括变量x2的第一边际熵变化率和变量x2的第二边际熵变化率；

35、变量x2的第一边际熵变化率的计算公式如下：

36、；

37、式中，表示在当前时间段(ti,ti+δt)内，处于ti+δt时刻时，在排除变量x1对变量x2影响的情况下，其他变量对变量x2产生影响时的边际熵，即变量x2的第一边际熵；表示随时间的变化率，即变量x2的第一边际熵变化率；表示在当前时间段(ti,ti+δt)内，处于ti+δt时刻时，在排除变量x1对变量x2影响的情况下，变量x2的边际概率密度函数；

38、变量x2的第二边际熵变化率的计算公式如下：

39、；

40、式中，表示在当前时间段(ti,ti+δt)内，处于ti+δt时刻时，在排除变量x3对变量x2影响的情况下，其他变量对变量x2产生影响时的边际熵，即变量x2的第二边际熵；表示随时间的变化率，即变量的第二边际熵变化率；表示在当前时间段(ti,ti+δt)内，处于ti+δt时刻时，在排除变量x3对变量x2影响的情况下，变量x2的边际概率密度函数；

41、变量x3的边际熵变化率包括变量的第一边际熵变化率和变量的第二边际熵变化率；

42、变量x3的第一边际熵变化率的计算公式如下：

43、；

44、式中，表示在当前时间段(ti,ti+δt)内，处于ti+δt时刻时，在排除变量x2对变量x3影响的情况下，其他变量对变量x3产生影响时的边际熵，即变量x3的第一边际熵；表示随时间的变化率，即变量x3的第一边际熵变化率；表示在当前时间段(ti,ti+δt)内，处于ti+δt时刻时，在排除变量x2对变量x3影响的情况下，变量x3的边际概率密度函数；

45、变量的第二边际熵变化率的计算公式如下：

46、；

47、式中，表示在当前时间段(ti,ti+δt)内，处于ti+δt时刻时，在排除变量x2对变量x3影响的情况下，其他变量对变量x3产生影响时的边际熵，即变量x3的第二边际熵；表示随时间的变化率，即变量x3的第二边际熵变化率；表示在当前时间段(ti,ti+δt)内，处于ti+δt时刻时，在排除变量x2对变量x3影响的情况下，变量x3的边际概率密度函数。

48、作为本发明的再进一步技术方案：变量x2向变量x1输送的信息流量，计算公式如下：

49、；

50、式中，表示在当前时间段(ti,ti+δt)内，处于ti+δt时刻时，变量x2向变量x1输送的信息流量；

51、变量x1向变量x2输送的信息流量，计算公式如下：

52、；

53、式中，表示在当前时间段(ti,ti+δt)内，处于ti+δt时刻时，变量x1向变量x2输送的信息流量；

54、变量x2向变量x3输送的信息流量，计算公式如下：

55、；

56、式中，表示在当前时间段(ti,ti+δt)内，处于ti+δt时刻时，变量x2向变量x3输送的信息流量；

57、变量x3向变量x2输送的信息流量，计算公式如下：

58、；

59、式中，表示在当前时间段(ti,ti+δt)内，处于ti+δt时刻时，变量x3向变量x2输送的信息流量；

60、变量x1向变量x3输送的信息流量，计算公式如下：

61、；

62、式中，表示在当前时间段(ti,ti+δt)内，处于ti+δt时刻时，变量x1向变量x3输送的信息流量。

63、作为本发明的再进一步技术方案：因果指向判断准则具体表示如下：

64、第一判断条件a：当第一判断条件a的各个判断式均成立时，变量x1、变量x2和变量x3之间的因果指向为：x1→x2→x3；第一判断条件a具体表示如下：

65、；

66、第二判断条件b：当第二判断条件b的各个判断式均成立时，变量x1、变量x2和变量x3之间的因果指向为：x1←x2→x3；第二判断条件b具体表示如下：

67、；

68、第三判断条件c：当第三判断条件c的各个判断式均成立时，变量x1、变量x2和变量x3之间的因果指向为：x1→x2←x3；第三判断条件c具体表示如下：

69、。

70、与现有技术相比，本发明的有益效果是：

71、1、本发明结合骨架生成与因果定向进行因果结构生成，考虑时间变化下，数据之间的因果方向的确定问题。利用fci算法对数据进行预处理，预处理结果表现出马尔科夫等价类，然后借用信息流的概念，通过对动力学系统进行建模，采用非对称信息机制，定量刻画信息在因果变量之间的传递，对建立的数学模型中直接因果对进行因果定向，最后生成唯一确定因果结构图，进而有效地提高因果图生成的准确性。