双点预瞄驾驶员模型参数识别方法

本发明涉及汽车驾驶，具体涉及一种双点预瞄驾驶员模型参数识别方法。

背景技术：

1、驾驶员模型可以从控制的角度模拟人类驾驶员的操作行为，如转向、加速和制动等，被广泛应用于车辆仿真系统开发、主动安全控制系统设计和智能车辆控制系统设计。要构建能准确模拟、描述驾驶员转向特性的驾驶员模型，就必须保证可以高效准确地识别驾驶员的转向特性参数，这也是车辆拟人控制系统开发中的必要环节。

2、驾驶员的转向特性参数一般包括预瞄时间、大脑反应时间和肌肉延迟时间等，不同的驾驶员模型会用不同类型和数量的参数进行描述。驾驶员的转向特性参数识别方法包括离线识别方法和在线识别方法。驾驶员转向特性参数离线识别方法常用于驾驶员模型的验证和相关数据的采集，驾驶员转向特性参数在线识别方法常用于智能车辆控制系统的开发，要求实时性好、精确度高。

3、目前常用的驾驶员转向特性参数在线识别包括基于最小二乘法的在线识别方法和基于传感器测量的在线识别方法。基于最小二乘法的在线识别方法会因数据维度高导致算力需求大从而实时性较差。基于传感器测量的在线识别方法需借助穿戴传感器，如眼动仪、肌电传感器等实现，实用性差且价格高昂。

技术实现思路

1、本发明提出了一种双点预瞄驾驶员模型参数识别方法，以解决现有技术对算力需求大或需要穿戴传感器进行数据采集的技术问题。

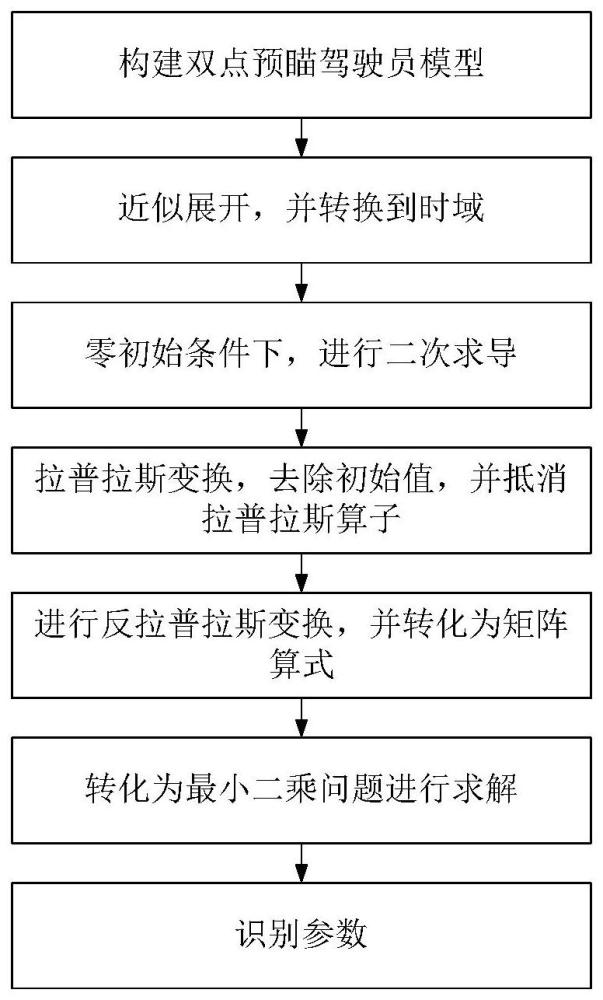
2、为解决上述技术问题，本发明提供了一种双点预瞄驾驶员模型参数识别方法，包括以下步骤：构建双点预瞄驾驶员模型；对所述双点预瞄驾驶员模型中的近似展开，并转换到时域，td1表示驾驶员肌肉延迟时间，s表示拉普拉斯算子；在零初始条件下，进行二次求导；进行拉普拉斯变换；去除拉普拉斯变换过程中产生的初始值，并对拉普拉斯算子进行抵消；进行反拉普拉斯变换，并转化为矩阵算式；将所述矩阵算式转化为最小二乘问题进行求解，识别所述双点预瞄驾驶员模型中的未知参数。

3、优选地，所述双点预瞄驾驶员模型的表达式为：

4、

5、式中，θfar为远视角，θfar≈lfarρ，lfar为驾驶员距道路边界预瞄点的距离，lfar＝tpvx，ρ为道路曲率，tp为驾驶员预瞄时间，vx为车辆纵向速度，θnear为近视角，lnear为驾驶员距道路中心线预瞄点的距离，lnear＝0.4lfar，ey为车辆的侧向位移误差，车辆的航向角误差；kp和kc为两个增益系数；td1为驾驶员肌肉延迟时间，td2为驾驶员神经反应延迟时间；s为拉普拉斯算子；tl表示时间常数。

6、优选地，转化为时域后δsw表达式为：

7、

8、

9、td＝td1+td2。

10、优选地，进行二次求导后的表达式为：

11、

12、优选地，进行拉普拉斯变换的表达式为：

13、

14、式中，is表示转向系统传动比，δsw(0)、θnear(0)和θfar(0)表示未知初始条件。

15、优选地，去除拉普拉斯变换过程中产生的初始值，并对拉普拉斯算子进行抵消的方法包括：对拉普拉斯变换的方程求关于拉普拉斯算子s的二阶导数后将等式两边同时乘以s-2，以消除初始值，并对拉普拉斯算子进行抵消。

16、优选地，等式两边同时乘以s-2的表达式为：

17、

18、优选地，转化为矩阵算式的方法包括：

19、通过反拉普拉斯变换，得到时域中的表达式：

20、

21、带入θfar和θnear得到：

22、

23、令：

24、

25、

26、得到矩阵算式：

27、q(t)＝p(t)n(t)；

28、式中，p(t)＝[p1(t) … p6(t)]，n(t)＝[n1(t) ... n6(t)]t。

29、优选地，求解的过程包括：

30、将所述矩阵算式转化为最小二乘问题：

31、

32、式中，t表示时间，j表示优化目标函数；

33、定义如下矩阵：

34、

35、转化为：

36、j(ν(t))＝mqq(t)-mqp(t)ν(t)-ν(t)tmpq(t)+ν(t)tmpp(t)ν(t)

37、＝[ν(t)-(mpp(t))-1mpq(t)]tmpp(t)[ν(t)-(mpp(t))-1mpq(t)]

38、+mqq(t)-mqp(t)(mpp(t))-1mpq(t)；

39、进行最小化最优解进行解析：

40、

41、优选地，识别得到的未知参数的表达式为：

42、

43、本发明的有益效果至少包括：所提出的驾驶员识别方法是通过对构建的双点预瞄驾驶员模型进行解算得到，所提出的参数识别方法不依赖于李雅普诺夫稳定性理论，识别过程没有渐近收敛阶段，可在短时间内迅速收敛，算力需求小；此外，本发明不需要借助穿戴传感器，实用性好。

技术特征：

1.一种双点预瞄驾驶员模型参数识别方法，其特征在于：包括以下步骤：构建双点预瞄驾驶员模型；对所述双点预瞄驾驶员模型中的近似展开，并转换到时域，td1表示驾驶员肌肉延迟时间，s表示拉普拉斯算子；在零初始条件下，进行二次求导；进行拉普拉斯变换；去除拉普拉斯变换过程中产生的初始值，并对拉普拉斯算子进行抵消；进行反拉普拉斯变换，并转化为矩阵算式；将所述矩阵算式转化为最小二乘问题进行求解，识别所述双点预瞄驾驶员模型中的未知参数。

2.根据权利要求1所述的一种双点预瞄驾驶员模型参数识别方法，其特征在于：所述双点预瞄驾驶员模型的表达式为：

3.根据权利要求2所述的一种双点预瞄驾驶员模型参数识别方法，其特征在于：转化为时域后δsw表达式为：

4.根据权利要求3所述的一种双点预瞄驾驶员模型参数识别方法，其特征在于：进行二次求导后的表达式为：

5.根据权利要求4所述的一种双点预瞄驾驶员模型参数识别方法，其特征在于：进行拉普拉斯变换的表达式为：

6.根据权利要求5所述的一种双点预瞄驾驶员模型参数识别方法，其特征在于：去除拉普拉斯变换过程中产生的初始值，并对拉普拉斯算子进行抵消的方法包括：对拉普拉斯变换的方程求关于拉普拉斯算子s的二阶导数后将等式两边同时乘以s-2，以消除初始值，并对拉普拉斯算子进行抵消。

7.根据权利要求6所述的一种双点预瞄驾驶员模型参数识别方法，其特征在于：等式两边同时乘以s-2的表达式为：

8.根据权利要求7所述的一种双点预瞄驾驶员模型参数识别方法，其特征在于：转化为矩阵算式的方法包括：

9.根据权利要求8所述的一种双点预瞄驾驶员模型参数识别方法，其特征在于：求解的过程包括：

10.根据权利要求9所述的一种双点预瞄驾驶员模型参数识别方法，其特征在于：识别得到的未知参数的表达式为：

技术总结本发明提供了一种双点预瞄驾驶员模型参数识别方法，构建双点预瞄驾驶员模型；对所述双点预瞄驾驶员模型中的近似展开，并转换到时域，t<subgt;d1</subgt;表示驾驶员肌肉延迟时间，s表示拉普拉斯算子；在零初始条件下，进行二次求导；进行拉普拉斯变换；去除拉普拉斯变换过程中产生的初始值，并对拉普拉斯算子进行抵消；进行反拉普拉斯变换，并转化为矩阵算式；将所述矩阵算式转化为最小二乘问题进行求解，识别所述双点预瞄驾驶员模型中的未知参数。解算过程算力需求小且不需要借助穿戴传感器。技术研发人员：汪怡平,李学鋆,苏楚奇,刘珣,袁晓红受保护的技术使用者：武汉理工大学技术研发日：技术公布日：2024/6/13