一种基于时变时滞的马尔可夫跳跃系统的同步控制方法

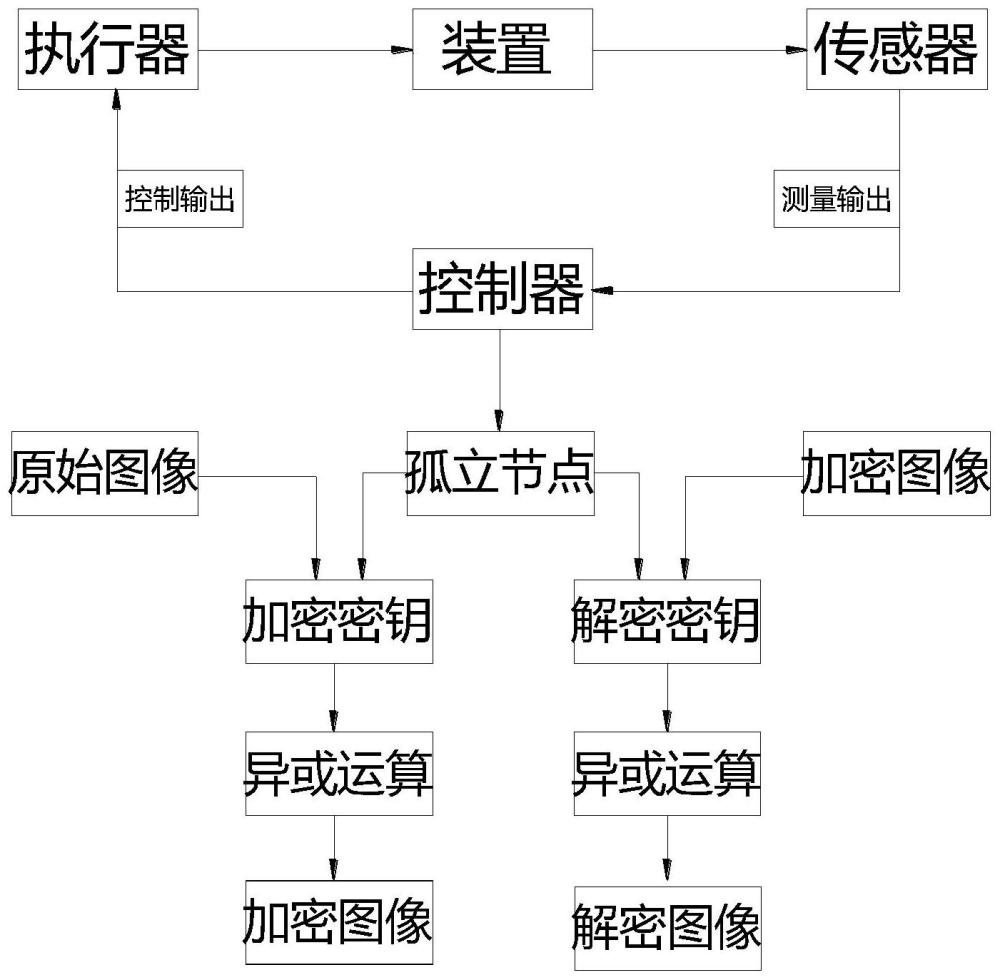
本发明涉及马尔科夫跳跃系统，具体涉及一种基于时变时滞的马尔可夫跳跃系统的同步控制方法。

背景技术：

1、近30年来专家学者开始研究复杂动态网络(cdn)的特性。cdn具有多种模型，由具有通过边或链接连接的顶点或节点的框架组成，并且具有巨大的应用和理论吸引力，特别是在经济学、工程科学和物理学领域。同步是cdn中的普遍现象，许多专家和学者致力于cdn同步控制问题。需要指出的是，复杂网络的拓扑连接在复杂环境下可能会遇到随机突变，这给其同步控制带来一些麻烦。幸运的是，马尔可夫过程可以有效地模拟上述拓扑结构的突变，马尔可夫跳跃复杂动态网络(mjcdn)的同步控制问题得到广泛的研究。

2、在实际应用中，直接测量系统状态是很困难的。考虑到这一点，利用输出信息进行反馈控制已成为一个主要的热点话题。主要研究成果可分为三类：基于观测器的输出反馈、动态输出反馈和静态输出反馈(sof)。由于sof控制具有结构简单、实现成本低的优点，因此得到广泛的研究。例如，在现有技术中，一些学者解决输出矩阵行满秩条件下的sof控制器设计问题。还一些学者在求解事件触发的sof同步控制问题时，要求lyapunov矩阵为对角结构。这些不同的约束对设计控制器的保守性有重大影响。针对控制器包含输入矩阵的情况，一些学者采用一种参数化方法，重点分离控制器的增益矩阵、输入矩阵和测量矩阵之间的耦合，以实现消除限制。虽然上述参数化方法可以消除对特定矩阵结构的要求以及对输入和输出矩阵的秩的约束，但使用一些不等式技术，这也会给控制器的设计带来一定的保守性。基于这种考虑，在没有输入矩阵的情况下，如何在不使用不等式缩放技术的条件下消除上述约束是设计静态输出反馈控制器时一个有趣的问题，也是发明的主要研究方向。

3、另一方面，随着数字和通信技术的快速进步，采样数据控制(sdc)在连续时间系统的研究中也受到高度关注。与传统的周期性采样或时间触发控制相比，sdc具有更多优势，例如，信息传输效率高、安装方便、可靠性高。sdc的研究可以分为两大类：离散时间方和输入延迟方法。其中，输入延迟方法作为分析和合成采样数据系统广泛采用的方法脱颖而出。然而，实际网络中的信号传输存在传输速度、带宽、协议等各种限制。由于这些限制，接收信号的设备可能会遇到不可避免的延迟。面对这种情况，一些研究人员考虑恒定延迟的周期性采样，并实现采样数据极值的搜索。相反，还一些研究人员考虑具有时变延迟的非周期采样，并实现与神经网络相关的sdc同步问题。相比之下，考虑时变延迟更现实。因此，在考虑采样延迟和时变延迟的同时考虑cdn的sof同步控制问题是一个具有挑战性的问题，也是当前研究工作的驱动力。为此，提出一种基于时变时滞的马尔可夫跳跃系统的同步控制方法。

技术实现思路

1、本发明所要解决的技术问题在于：如何在考虑采样延迟和时变延迟的同时考虑cdn的sof同步控制问题，通过基于控制器控制与h∞性能指标控制相结合的方式，可以实现在时变时滞的影响下通过静态输出反馈对系统的同步控制，提供了一种基于时变时滞的马尔可夫跳跃系统的同步控制方法。

2、本发明是通过以下技术方案解决上述技术问题的，本发明包括以下步骤：

3、s1：引入马尔可夫过程来模拟复杂动态网络拓扑中的随机突变现象；

4、s2：构建采样控制器模型，基于采样控制器模型和步骤s1的系统模型得到基于时变时滞的马尔可夫跳跃复杂动态网络的闭环系统模型；

5、s3：给出马尔可夫跳跃复杂动态网络系统在扰动下随机稳定且满足h∞性能指标的线性矩阵不等式条件；

6、s4：利用lyapunov函数和性能指标函数证明步骤s3的线性矩阵不等式条件有效；

7、s5：采用自由权矩阵与解耦方法相结合，求解出采样反馈控制器的增益矩阵；

8、s6：根据采样反馈控制器的增益矩阵和给定的系统参数实现对系统的同步控制。

9、更进一步地，在所述步骤s1中，具体处理过程如下：

10、s11：建立马尔可夫跳跃复杂动态网络系统模型如下：

11、

12、其中，xi、ui(t)∈rn，xi(t)和ui(t)分别表示第i个节点的状态变量和控制输入，zi(t)是控制输出，yi(t)是测量输出，b＝(bij)n×n∈rn×n和a＝(aij)n×n∈rn×n是节点之间的内部耦合矩阵，e＝(eij)n×n是复杂动态网络的外部耦合矩阵，ωi(t)是属于区间上的额外干扰，是传感器的测量矩阵，是马尔可夫跳跃复杂动态网络系统的输出矩阵，为时变时滞函数，且满足

13、s12：引入一个具有预定概率空间的连续时间马尔可夫链其在一个有限集合中取值，模式转换率矩阵

14、

15、其中，δt＞0，πmn≥0，并且为模式转移概率矩阵；

16、s13：当两个不同节点j和i之间存在连接时，表示当两个不同节点j和i之间不存在连接时，表示对角线位置的值满足以下等式：

17、

18、s14：令ei(t)＝xi(t)-v(t)为同步误差，其中，v(t)∈rn是非受迫孤立节点的状态轨迹，推导出马尔可夫跳跃复杂动态网络的同步误差系统表达式如下：

19、

20、其中，g(ei(t))＝f(xi(t))-f(v(t))，f(xi(t))为非线性函数。

21、更进一步地，在所述步骤s2中，具体处理过程如下：

22、s21：构建采样反馈控制器模型：

23、

24、其中，k是一组待设计的采样反馈控制器的增益矩阵，ei(tk)是ei(t)在采样时刻tk的测量值，假设对于任意整数k≥0有tk+1-tk＝βk≤β，β表示最大的采样间隔；

25、s22：将步骤s21中的采样反馈控制器模型带入步骤s11中的系统模型中，得到基于时变时滞的马尔可夫跳跃复杂动态网络的静态输出反馈控制的闭环系统模型如下：

26、

27、其中，ρ(t)＝t-tk，从而可以得到0≤ρ(t)≤β；

28、s23：将基于时变时滞的马尔可夫跳跃复杂动态网络的静态输出反馈控制的闭环系统模型简化如下：

29、

30、其中，et(t)＝[e1t(t),e2t(t),...,ent(t)]，k＝diag{k1,k2,...,kn}，ωt(t)＝[ω1t(t),ω2t(t),...,ωnt(t)]，表示克罗内克积；diag{·}表示对角矩阵。

31、更进一步地，在所述步骤s3中，具体处理过程如下：

32、s31：定义以下符号：

33、

34、

35、

36、

37、

38、s32：对于给定的标量β，κ，γ，δ，ε和σ∈[0,1]，已知矩阵r和s；如果存在可逆矩阵π，p1＞0，p2＞0，t1＞0，t2＞0，t3＞0，u1＞0，u2＞0，u3＞0，使得以下不等式成立：

39、

40、δ1≥0

41、δ2≥0

42、其中：

43、

44、

45、*表示矩阵中的对称块。

46、更进一步地，在所述步骤s4中，具体处理过程如下：

47、s41：选取lyapunov函数如下：

48、

49、s42：引入自由权矩阵如下：

50、

51、s43：选取性能指标函数如下：

52、

53、s44：利用上述的lyapunov函数、自由权矩阵、性能指标函数，基于李雅谱诺夫稳定性理论能够证明同步误差系统是随机稳定的，并且满足规定的混合的h∞性能指标和无源性能指标δ。

54、更进一步地，在所述步骤s5中，具体处理过程如下：

55、s51：令k＝π-tω，结合自由权矩阵；

56、s52：对于给定的标量β，κ，γ，δ，ε和σ∈[0,1]，已知矩阵r和s，如果存在可逆矩阵π，p1＞0，p2＞0，t1＞0，t2＞0，t3＞0，u1＞0，u2＞0，u3＞0，使得以下不等式成立：

57、

58、δ1≥0

59、δ2≥0

60、其中，

61、s53：利用仿真软件通过给定矩阵参数计算出增益矩阵k的值，实现复杂动态网络与孤立节点的同步。

62、本发明相比现有技术具有以下优点：该基于时变时滞的马尔可夫跳跃系统的同步控制方法，对于mjcdn，设计sof控制器，使得网络能够有效应对拓扑中的随机突变，此外，还考虑时变时延的情况，并结合输入时延方法，分析采样间隔和通信时延对系统的影响；与现有的一些sof控制技术相比，自由权矩阵结合新颖的解耦方法，避免了等式约束、对输出矩阵的秩的要求以及一些不等式的使用；通过基于控制器控制与h∞性能指标控制相结合的方式，可以实现在时变时滞的影响下通过静态输出反馈对系统的同步控制。