一种考虑随机和区间混合不确定性的PID控制器序贯可靠设计方法

本发明涉及振动控制及可靠性评估，具体涉及一种考虑随机和区间混合不确定性的pid控制器序贯可靠设计方法。

背景技术：

1、在实际工程中，振动主动控制是实际工程中的一个重要问题。预期之外的振动可能会降低实际系统的性能，甚至导致系统损坏。与被动振动控制相比，主动振动控制可以在不明显增加结构重量的情况下有效抑制振动和噪声，满足了实际工程、特别是航空航天领域的轻量化设计要求。设计主动控制器有各种成熟的经验方法或分析方法，例如比例积分微分(简称pid)控制、极点配置控制和最优控制。以上这些方法中，最优控制是指导控制器设计的常用方法，在最优控制中，控制器被设计为在满足响应极值或控制力极值或其他约束的同时使目标指数最小或最大。然而，在实际工程中存在各种不确定性，如传感器信号中的噪声信号、材料特性的分散性和测量误差，因此实际系统与理想理论模型相比存在误差。由于这些不确定性，根据确定性系统设计的最优控制器很可能不满足约束。在实际工程中，为系统设计控制器时应考虑不确定性。传统的鲁棒控制可以保证不确定系统的安全性，但设计的闭环系统往往过于保守、能耗大。因此，根据可靠性进行设计的方法被提出(即“可靠设计”)，以平衡不确定系统的安全性和能耗。

2、对于某些不确定性参数，它们的统计数据是足够的。在这种情况下，这些不确定性可以用概率密度函数量化，相应地，可以用概率论来评估可靠性。蒙特卡洛模拟将失效可能性定义为样本与总样本的比率。但蒙特卡洛模拟需要大量的样本数据，这限制了它在实际工程中的应用。cornell提出了一次二阶矩方法，其中可靠性指标是在正态分布和线性极限状态函数下建立的。然而，一次二阶矩方法缺乏不变性，因此提出了先进的一次二阶矩，其中非线性极限状态函数在设计点进行展开。rice首先提出了首次穿越理论来计算随机过程响应的概率可靠性。davenport在穿越次数为泊松分布的假设下求解了稳态响应随机过程极值的概率密度函数。vanmarcke在两状态马尔可夫过程的假设下求解极值的概率密度分布。li和chen提出了基于概率守恒原理的概率密度演化方法，得到了解耦的概率密度进化方程。在这种情况下，可以通过引入吸收边界条件并对联合概率密度函数进行积分来求解动态可靠性，或者构造虚拟随机过程并将可靠性的计算转化为一维积分问题。meng等人提出了一种半解析极值方法，通过扩展最优线性估计方法来模拟不同时刻之间的相关性，以此提高极值方法的计算效率。

3、然而，对于实际工程中动态系统的一些不确定性，样本不足，无法准确获得其概率密度函数，因此概率可靠性在这种情况下的应用受到限制。但它们的边界更容易获得，因此这些不确定性用非概率区间形式量化。ben haim和elishakoff首次提出了不确定性的非概率区间量化，相应地，近年来发展了考虑区间不确定性的可靠性。mahadevan和dey计算了具有自适应蒙特卡洛方法的脆性结构的时间依赖可靠性。wang等人进行了区间不确定振动控制系统的时变靠性研究，考虑了首次穿越理论和时间矩的相关性。chang等人提出了一种时间相关模型来估计具有区间误差的机械结构的安全性，其中将存在时间相关性的极限状态函数转换为与时间无相关性的极限状态函数。yang等人考虑结构阻力随时间变化的性能衰减和荷载时间效应，使用时间相关可靠性来评估梁结构的安全性。

4、实际工程中存在各种不确定性，由于样本数据、相关性等因素的影响，其合适的量化方法也不同，即存在混合不确定性。对于这些具有混合不确定性的不确定系统，其可靠性也是混合可靠性。wen等人提出了一种同时考虑概率和模糊不确定性的混合可靠性指标。ni和qiu提出了一种考虑概率和模糊不确定性的混合可靠性模型，该模型可以处理线性或非线性状态函数。shi等人考虑概率和模糊输入，提出了两个指标来从不同方面衡量时变结构的安全度。

5、但是目前的方法仍存在两个主要问题：(1)混合可靠度指标仅是作为系统安全性的度量标准，并未参与指导pid控制器的设计；(2)传统基于可靠度优化问题的双环求解策略中，可靠度分析和参数优化迭代存在耦合，导致优化求解效率严重低下。

技术实现思路

1、为解决上述技术问题，本发明提供一种考虑随机和区间混合不确定性的pid控制器序贯可靠设计方法，针对含不确定变量pid闭环控制系统，同时考虑随机不确定参数和区间不确定参数，进行不确定性系统的混合可靠度评估，并以混合可靠度为参考、采用序贯优化策略进行控制器最优设计。该方法可以用于存在多个混合不确定性参数、并且其中一些不确定参数的概率信息较少的pid闭环系统的控制器设计，所得控制器符合系统的混合可靠度要求，并且具有很高的求解效率。

2、为达到上述目的，本发明采用的技术方案为：

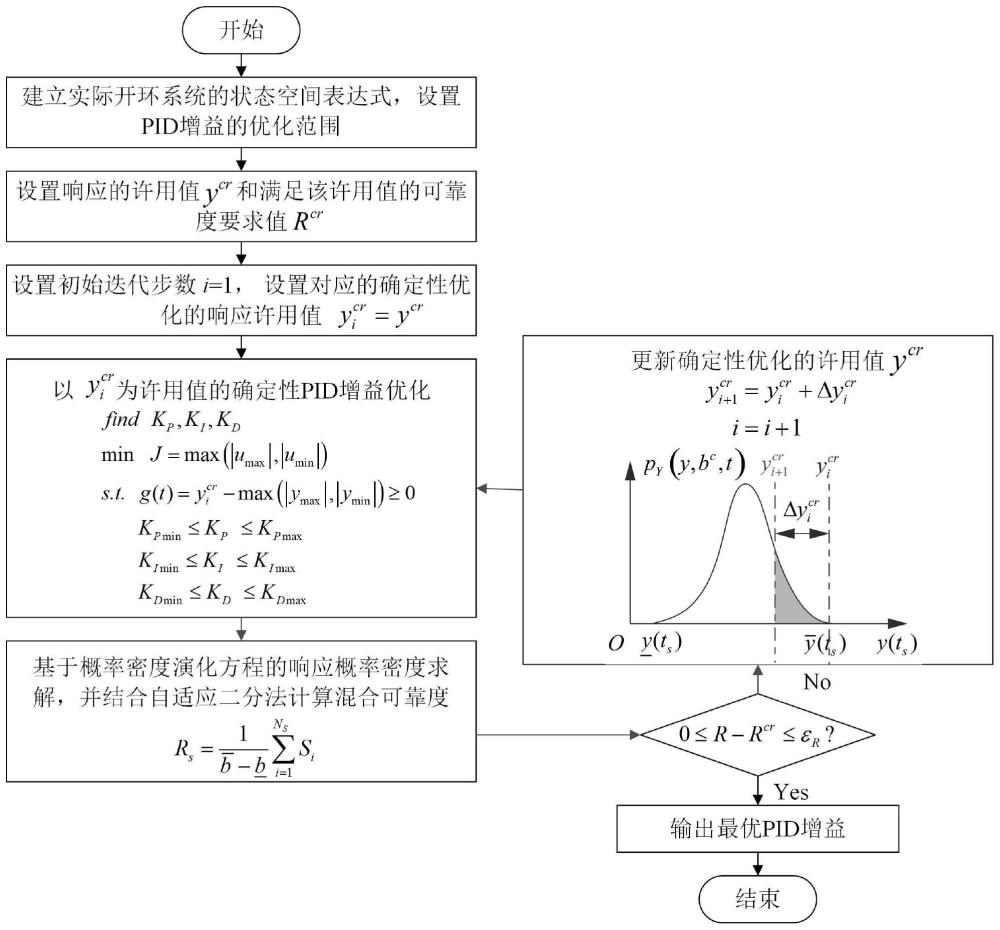
3、一种考虑随机和区间混合不确定性的pid控制器序贯可靠设计方法，针对含随机和区间不确定变量pid闭环控制系统，通过将不确定变量进行概率和非概率区间化描述，计算混合可靠度并以此进行控制器最优设计，包括如下步骤：

4、第一步：根据实际工程系统建立对应的状态空间表达式以及确定性系统；所述确定性系统为不考虑不确定性，各参数均取名义值的系统；

5、第二步：设随机不确定参数为θ，区间不确定参数为b，其中概率不确定参数通过概率密度函数pθ(θ)进行定量化描述，区间不确定参数通过区间数学形式进行定量化描述；

6、第三步：通过自适应二分法结合概率密度演化方程计算混合可靠度；

7、第四步：由于混合可靠度反映不确定性系统的安全性，将原确定性优化列式中的极限状态函数更换为可靠度约束，从而体现不确定性对于系统安全性的影响。

8、进一步地，所述的第一步包括：

9、设n自由度控制系统系统得到的状态空间为：

10、

11、y(t)＝cz(t)

12、其中，t为时间，u(t)为施加的控制力，f(t)为扰动外载荷，z(t)为状态向量，为状态向量对时间的导数，y(t)为输出向量，a为状态传递矩阵，b和e分别为控制力和扰动外载荷的输入矩阵，c为输出矩阵；

13、针对确定性系统的pid增益最优设计表达式写为：

14、寻找kp,ki,kd

15、min j＝max(|umax|,|umin|)

16、s.t. g(t)＝ycr-max(|ymax|,|ymin|)≥0

17、kpmin≤kp≤kpmax

18、kimin≤ki≤kimax

19、kdmin≤kd≤kdmax

20、其中，kpmax、kimax、kdmax、kpmin、kimin和kdmin分别为kp、ki、kd的设计域上下界，g(t)为极限状态函数，ycr为响应许用值，取绝对值；[t0 tf]为所关注的时间段；响应的最大峰值为ymax，取绝对值；响应的最大谷值为ymin，取绝对值；控制力指标j通过施加的控制力u(t)的峰值umax和谷值umin表示，均取绝对值。

21、进一步地，所述第二步中的定量化描述为：

22、b＝[bl bu]＝[bc-br bc+br]

23、其中，bl和bu分别为不确定区间参数的下界和上界，bc和br分别为不确定参数的中心值和半径；对于单输出系统，结合n自由度系统得到的状态空间表达式，考虑混合不确定性(θ,b)的系统表示为：

24、

25、y(θ,b,t)＝c(θ,b)z(θ,b,t)

26、给定区间不确定参数b的第j个样本点bj∈[bl bu]，其中bl和bu分别为bj的下界和上界，原不确定性系统简化为只存在随机不确定参数的系统，采用考虑失效的概率密度演化方程进行求解：

27、

28、其中，pyθ(y,θ,bj,t)为响应y(t)和随机不确定参数θ在样本点下的联合概率密度函数，是相应的速度矢量；h[·]为阶跃函数，即：

29、

30、当系统响应超过许用值时系统失效，响应概率分布通过对pyθ(y,θ,bj,t)在随机不确定参数θ的分布域ωθ上的积分得到，概率密度函数py(y,bj,t)为：

31、

32、此时在任意时刻t的概率可靠度rp(bj,t)表示为：

33、

34、其中，pr(·)表示事件发生的概率，ωs表示安全域，t0为存在可靠度要求的初始时刻，y(τ)为时间段t0≤τ≤t内的响应。

35、进一步地，所述第三步包括：

36、混合表示为概率可靠度曲线与区间变量横坐标轴在区间[bl bu]之间围成的面积；之后通过自适应二分法在区间[bl bu]内选取合适的样本点，将积分运算近似离散为若干梯形面积求和；

37、设任一区间[b1 b2]的二分点为s表示[b1 b2]内的近似梯形面积，s1表示[b1 b3]内的近似梯形面积，s2表示[b3 b2]内的近似梯形面积：

38、s1＝0.5(rp(b1)+rp(b3))(b3-b1)

39、s2＝0.5(rp(b2)+rp(b3))(b2-b3)

40、s＝0.5(rp(b1)+rp(b2))(b2-b1)

41、当以下不等式满足时，判定二分收敛，则无需添加新样本点，其中εs为预先设置的收敛阈值：

42、|s-(s1+s2)|＜εs

43、若上述不等式不满足，则对不满足的区间继续添加二分点，重复第三步，直至所有区间均符合收敛准则，由此得到一系列区间不确定参数的样本点；

44、设所得样本点将原积分区域离散为ns个梯形，混合可靠度r由各个近似梯形的面积si求和进行近似计算：

45、

46、进一步地，所述第四步包括：

47、寻找kp,ki,kd

48、min j＝max(|umax|,|umin|)

49、s.t.r≥rcr

50、kpmin≤kp≤kpmax

51、kimin≤ki≤kimax

52、kdmin≤kd≤kdmax

53、其中，rcr为可靠度要求的许用值；

54、采用序贯优化求解策略进行求解，包括：在第i个给定许用值的情况下，重复第一步至第三步得到确定性优化得到的pid增益下的混合可靠度r；

55、判断计算得到的混合可靠度r是否符合如下收敛准则：

56、0≤r-rcr≤εr

57、其中，εr为预先设置的收敛阈值；

58、若上式符合收敛准则，则说明优化收敛，反之则根据可靠度迭代下一步，即第i+1步确定性优化的响应许用值：

59、

60、其中，为两步确定性优化中响应许用值的变化量，其值通过响应超过许用值前一时刻，即可靠度小于1或者响应绝对值最大值时刻，即可靠度等于1的静态可靠度η进行调整，静态可靠度η的计算方法为：

61、峰值绝对值大于谷值绝对值：

62、

63、峰值绝对值小于谷值绝对值：

64、

65、其中，stotal和sshadow分别是响应的概率密度函数py(y,bj,t)与横轴围成的总面积和阴影部分面积，通过对概率密度函数的积分进行求解；

66、重复第二步至第四步，直至达到混合可靠度r的收敛准则或者最大迭代步数，由此得到能耗最小且符合安全性要求的最优pid增益。

67、进一步地，所述的第二步中，给定区间不确定参数样本点，通过概率密度演化方程求解响应和随机不确定参数的联合概率密度函数，在考虑失效的情况下通过积分求解概率可靠度，实现概率可靠度的实时评估。

68、进一步地，所述的第三步中使用第二步中计算得到的概率可靠度rp(bj,t)，采用自适应二分法在区间不确定参数内选取合适的样本点，将混合可靠度定义为概率可靠度在区间上的均值，实现混合可靠度兼顾效率和高精度的求解。

69、进一步地，所述的第四步中，通过定义第一步中的控制力指标j最小和第三步得到的混合可靠度作为约束构建优化列式，通过序贯优化策略提高优化列式求解效率，得到符合要求的pid参数。

70、有益效果：

71、(1)本发明在前三步进行的混合可靠度分析，可以有效评估不确定性系统的安全性，并在第四步中通过在优化列式中引入混合可靠度约束，将混合可靠度用于指导pid控制器的设计；

72、(2)本发明在第四步中采用序贯优化策略，通过响应许用值迭代使得混合可靠度评估与确定性系统的pid控制器优化设计相解耦，实现了优化的高效求解。