一种无人步履式挖掘机姿态平稳性最优控制方法及系统

本发明涉及机器人控制领域，涉及一种无人步履式挖掘机姿态平稳性最优控制方法及系统。

背景技术：

1、步履式挖掘机作为一种全地形、多用途步行式挖掘机，被广泛用于山地、丘陵、森林等复杂地形环境中的作业任务。相比于传统履带式挖掘机，步履式挖掘机底盘通过四个独立的步行机构用来调节车身的平衡，因此使挖掘机的适用性和稳定性大大提高。近年来，为应对山地、森林等复杂环境下的作业任务，步履式挖掘机正朝着智能化、无人化的方向发展，其中挖掘机姿态平稳性控制成为了无人化开发过程中的具有较大难度挑战的技术。由于作业场景中地形起伏复杂，容易导致运动过程颠簸较大、能耗较高甚至车身倾翻等情况的发生，目前挖掘机控制算法难以根据实际复杂地形高效准确的调控车身姿态，存在自主作业过程中的安全性问题。

技术实现思路

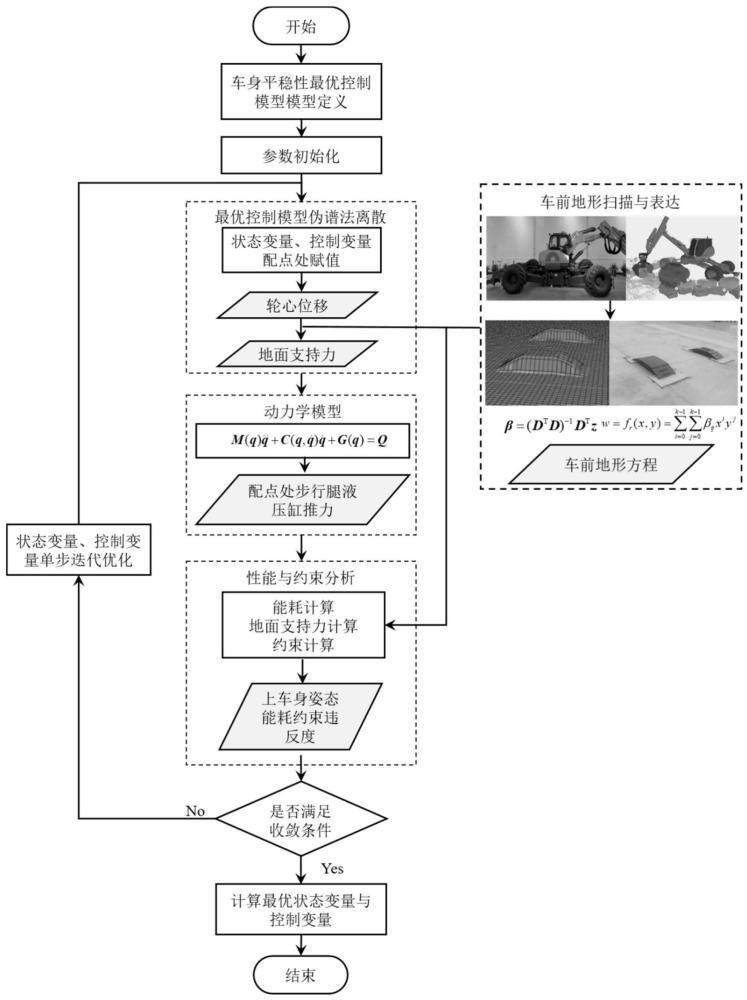
1、为了解决现有技术中存在的上述问题，本发明的目的在于提出一种无人步履式挖掘机姿态平稳性最优控制方法，能够获得四个支撑腿处液压缸最优的运动轨迹和输出力序列，实现在实际复杂地形中高效准确的调控无人步履式挖掘机车身姿态，对于保证无人步履式挖掘机自主作业过程中的安全性，提高作业质量具有重要意义。

2、为实现上述技术目的，本案的技术方案具体如下。

3、第一方面，本案提出一种无人步履式挖掘机姿态平稳性最优控制方法，所述方法包括下述步骤：

4、将系统广义坐标定义为其中，zs为上车身垂向位移，θs为上车身俯仰角，为上车身侧倾角，θ1，θ2，θ3，θ4分别为左前、左后、右前、右后支撑腿液压缸与回转底盘夹角；令运动时域t的状态变量将四腿处液压缸输出力fi(t)(i＝1，2，3，4)作为系统控制变量u(t)，将状态变量x(t)、控制变量u(t)和系统运行时间tf同时作为优化变量xopt：

5、

6、建立车身平稳性最优控制模型的目标函数：

7、

8、式中：vi为第i个支撑腿液压缸伸缩速度；

9、所述目标函数需满足约束条件包括：动力学约束、在姿态调整过程中步履式挖掘机四个支撑腿液压缸伸缩速度需要保证在最大允许下限和上限之间、运动过程中四腿轮胎中心处位移与各轮所对应路边高程差值需要保持在最大允许下限和上限之间、轮胎支持力限制在最小允许值和最大允许值之间、四腿处液压缸输出力在最小允许值和最大允许值之间；

10、获取使目标函数取得最小值的优化变量，从而获得四个支撑腿处液压缸最优的运动轨迹和输出力序列实现无人步履式挖掘机的平稳性控制；

11、其中：为第p组左前、左后、右前、右后支撑腿液压缸与回转底盘夹角值，为第p组左前、左后、右前、右后四腿处液压缸输出力值。

12、在上述技术方案的一种实施方式中，采用伪谱离散方法将连续最优控制模型变量在lgr配点处离散，从而将求解最优控制模型的最优控制问题转化为非线性规划问题。

13、在上述技术方案的一种实施方式中，轮胎支持力通过轮胎力计算，在计算轮胎力时，将轮胎近似为弹簧阻尼系统，采用下式计算：

14、

15、式中：fwi(t)为轮胎支持力，zui为轮胎铰接点处中心位移，由上车姿态与液压缸角度通过运动学关系获得，kw、cw分为轮胎刚度与阻尼，wi(t)为第i个轮胎所在的路面高程。

16、在上述技术方案的一种实施方式中，所述路面高程通过建立车前地形的数学解析表达式获取，步骤包括：

17、利用激光雷达扫描地形环境，获取无人步履式挖掘机周围地形点云；

18、通过区域生长法分割获取车前地形点云p＝[x，y，z]，其中，x＝[x1，x2，…xm]t，y＝[y1，y2，…ym]t，z＝[x1，x2，…zm]t，m为点云数目；

19、采用多项式响应面回归方法，建立车前地形x，y方向与高程z方向上的函数关系表达式；

20、将m个点云代入函数关系表达式，利用最小二乘法建立多项式响应面回归预测模型，从而获得车前地形任意水平坐标(x，y)下的路面高程。

21、第二方面，本案提出一种计算机可读存储介质，存储有能够被处理器加载并执行上述任一种所述方法的计算机程序。

22、第三方面，本案根据上述方法技术方案，实现了一种无人步履式挖掘机姿态平稳性最优控制系统，具体地：

23、所述系统的广义坐标定义为其中，zs为上车身垂向位移，θs为上车身俯仰角，为上车身侧倾角，θ1，θ2，θ3，θ4分别为左前、左后、右前、右后支撑腿液压缸与回转底盘夹角；

24、所述系统在运动时域t的状态变量为控制变量u(t)为四腿处液压缸输出力fi(t)(i＝1，2，3，4)，所述系统将状态变量x(t)、控制变量u(t)和系统运行时间tf同时作为优化变量xopt：

25、

26、所述系统通过求解下述车身平稳性最优控制模型获得优化变量，从而获得四个支撑腿处液压缸最优的运动轨迹和输出力序列实现无人步履式挖掘机的平稳性控制；

27、车身平稳性最优控制模型的目标函数为：

28、

29、式中：vi为第i个支撑腿液压缸伸缩速度。

30、所述目标函数需满足约束条件包括：动力学约束、在姿态调整过程中步履式挖掘机四个支撑腿液压缸伸缩速度需要保证在最大允许下限和上限之间、运动过程中四腿轮胎中心处位移与各轮所对应路边高程差值需要保持在最大允许下限和上限之间、轮胎支持力限制在最小允许值和最大允许值之间、四腿处液压缸输出力在最小允许值和最大允许值之间；

31、其中：为第p组左前、左后、右前、右后支撑腿液压缸与回转底盘夹角值，为第p组左前、左后、右前、右后四腿处液压缸输出力值。

32、本案的有益技术效果为：(1)本案构建了最优控制模型，可以求解四个支撑腿处液压缸最优的运动轨迹和输出力序列。(2)在求解时，利用离散方法将最优控制模型转化为非线性规划问题，使得计算方便易实施。(3)利用激光雷达扫描地形环境，并获得车前地形的数学解析表达，实现高效准确调控实际复杂地形中的无人步履式挖掘机车身姿态，对于保证无人步履式挖掘机自主作业过程中的安全性，提高作业质量具有重要意义。

技术特征：

1.一种无人步履式挖掘机姿态平稳性最优控制方法，其特征在于：

2.根据权利要求1所述的方法，其特征在于，采用伪谱离散方法将连续最优控制模型变量在lgr配点处离散，从而将求解最优控制模型的最优控制问题转化为非线性规划问题。

3.根据权利要求1所述的方法，其特征在于，轮胎支持力通过轮胎力计算，在计算轮胎力时，将轮胎近似为弹簧阻尼系统，采用下式计算：

4.根据权利要求3所述的方法，其特征在于，所述路面高程通过建立车前地形的数学解析表达式获取，步骤包括：

5.一种计算机可读存储介质，其特征在于：存储有能够被处理器加载并执行如权利要求1至4中任一种所述方法的计算机程序。

6.一种无人步履式挖掘机姿态平稳性最优控制系统，其特征在于：

7.根据权利要求6所述的系统，其特征在于：采用伪谱离散方法将连续最优控制模型变量在lgr配点处离散，从而将求解最优控制模型的最优控制问题转化为非线性规划问题。

8.根据权利要求6所述的系统，其特征在于：轮胎支持力通过轮胎力计算，在计算轮胎力时，将轮胎近似为弹簧阻尼系统，采用下式计算：

9.根据权利要求8所述的系统，其特征在于：所述路面高程通过建立车前地形的数学解析表达式获取，步骤包括：

技术总结本案涉及一种无人步履式挖掘机姿态平稳性最优控制方法及系统，属于机器人控制领域，用于解决目前挖掘机控制算法难以根据实际复杂地形高效准确的调控车身姿态，存在自主作业过程中的安全性问题。本方案针对无人步履式挖掘机建立了最优控制模型，可提高求解四个支撑腿处液压缸最优的运动轨迹和输出力序列的准确度。在求解时，利用离散方法将最优控制模型转化为非线性规划问题，使得计算方便易实施。并且，利用激光雷达扫描地形环境，并获得车前地形的数学解析表达，有利于在在实际复杂地形中高效准确的调控无人步履式挖掘机车身姿态，对于保证无人步履式挖掘机自主作业过程中的安全性，提高作业质量具有重要意义。技术研发人员：张天赐,赵丁选,王子鹤,郭瑞,倪涛受保护的技术使用者：燕山大学技术研发日：技术公布日：2024/7/15