包括盲旋转的加密计算的制作方法

当前公开的主题涉及一种密码加密计算方法、一种确定测试多项式的方法、相应的设备以及一种计算机可读介质。

背景技术：

1、同态密码学允许人们执行加密计算：由一方对加密数据执行该计算(例如，电路评估)而该方无法解密。例如，输入数据和计算结果可以以加密形式接收和返回。中间数据(例如，计算的内部状态)也可以采用加密形式。

2、即使计算的结果以加密形式返回，在解密时，预计输出会与对未加密数据执行运算相同或非常接近。同态加密可被用于保护隐私的外包存储和计算。这允许数据被加密且被外包到云环境，以进行处理和/或存储，同时加密。

3、例如，同态密码学可被应用在诸如医学保健的领域中，在这些领域中，隐私法规可能使得共享明文数据变得困难，但是对加密医学数据的计算可能是允许的。例如，被开发如用于对医学数据进行分类的医学模型可以被配置为从第三方(如，医院)接收加密形式的医学数据。医学模型可以例如将医学数据分类为例如正常的或异常的，或者分类为具有某种特定的医学综合征、疾病或其他病症。使用同态加密，医学模型可被应用于接收加密形式的医学数据。这意味着提供医学模型的一方无法访问与加密医学数据相对应的明文医学数据。该服务的用户可以对医学模型应用的结果进行解密。

4、特别是，存在至少在原理上可用于计算加密数据的任何函数的同态密码技术。此类技术被称为“全同态加密”(fhe)技术。

5、出于安全原因，fhe的已知实施方式使用噪声密文。例如，数据项的加密可以包括将数据项映射到密钥相关格中的点，向该点添加噪声。特别是，fhe的许多已知实施方式使用lwe类型密文，lwe类型密文的安全性取决于容错学习问题的加密难度。这种lwe类型密文可以包括一个或多个掩码值(例如，按某个模数q取模的值，或环面元素)，加上主体值，所述主体值使用加密密钥从掩码值以及明文中导出，并且所述主体值包含噪声。它的一个变体是glwe类型密文，所述glwe类型密文加密并使用多项式而不是标量值。fhe的其他已知实施方式使用ntru类型密文，其基本适用相同的考虑。

6、当数据项刚刚被加密时，噪声很低——加密是新近的。例如，噪声量很低，使得如果要解密数据项，则可以在解密过程中的某个点去除噪声，例如通过舍入。另一方面，噪声应该足够高，以使对系统的攻击足够困难。例如，在假设没有噪声的情况下，许多同态加密方案可能会受到线性代数或其他有效算法(例如，格规约算法)的攻击。当数据项被加密时，会添加经过选择的噪声，使得攻击是困难的，同时仍然可以执行同态运算，并且解密仍然是可能的。

7、大多数同态运算都会增加同态加密数据项中固有的噪声。当许多这样的运算被执行时，噪声可能达到不再可能进行唯一解密的水平。一般来说，已知使用称为自举的技术来降低同态加密值的噪声。自举可以使用称为自举密钥的公钥。通过在需要时使用自举来降低噪声，原理上可以计算任何所需数目的同态运算。

8、一种特殊类别的全同态加密方案是tfhe类的同态加密方案。这样的方案在i.chillotti等人的“programmable bootstrapping enables efficient homomorphicinference of deep neural networks”,cyber security cryptography and machinelearning(cscml 2021),lecture notes in computer science的第12716卷,第1-19页，springer,2021(通过引用纳入本文)中被描述。tfhe类方案与其他fhe方案的不同之处在于，它们支持一种相对非常高效的自举技术；此外，它们还能够在自举运算过程中同时对函数进行评估，被称为可编程自举。常规自举与带有标识函数的可编程自举相对应。

9、这种可编程自举技术可以通过执行所谓的盲旋转来降低密文(例如，lwe类型密文)中的噪声。盲旋转可以使用所定义的测试多项式使得其每个系数对对应于经缩放的明文值i的期望输出值进行编码。盲旋转可能涉及对加密的自举单项式(例如，glwe加密)的指数的解密(例如，lwe解密)进行同态评估，从而产生测试多项式与自举单项式的加密的(例如，glwe加密的)多项式乘积所产生的多项式乘积被加密为按模数q＝2ω以及多项式xn+1取模的密文，其中n是2的幂。可以确保经缩放的明文值的最高有效位设定为0。在这种情况下，多项式乘积将的期望输出值作为其常数系数。这是因为加密是按商多项式xn+1取模来定义的。也就是说，由于商多项式xn+1的这个具体选择，恒等式xk＝-xk+n成立，因此然后可以提取该系数，以获得期望输出值的加密。

10、有趣的是，盲旋转的输出具有与输入密文中的噪声无关的噪声量。因此，通过执行包括盲旋转的可编程自举，可以将输入密文中的噪声降低到固定量，而可能同时将函数应用于输入密文。通过在适当的时间执行可编程自举，可以执行无限乘法复杂度的加密计算。

11、已知的可编程自举，特别是其盲旋转，具有许多限制。首先，盲旋转通常要求将经缩放的明文值的最高有效位设定为0，换句话说，可对其值进行编程的明文的比率仅为1/2。其次，已知的盲旋转需要计算大量按模数q＝2ω以及多项式xn+1取模的多项式乘积，其中n是2的幂。这种多项式乘法的计算成本很高，使得盲旋转以及因此可编程自举的计算成本仍然相对较高。

技术实现思路

1、根据本发明的一方面，提供了如权利要求所定义的一种密码加密计算方法。根据本发明的另一方面，提供了如权利要求所定义的一种确定在这种加密计算方法中所使用的测试多项式的方法。根据另一些方面，提供了如权利要求所定义的与这些计算机实施方法相对应的设备。根据另一方面，提供了如权利要求所定义的一种计算机可读介质。

2、加密计算可能涉及执行密文(例如，lwe类型密文)的盲旋转；例如作为可编程自举的一部分。密文可以对某个明文加密，例如原始密文的缩放。盲旋转可以计算测试多项式与多项式环中将明文值表示为指数的自举单项式(例如，)的加密多项式乘积，例如

3、盲旋转可能涉及计算多项式环中的多个多项式乘积。在现有技术中，该多项式环是按模数q以及商多项式xn+1取模的环其中q和n都是2的幂。发明人意识到，由于多项式乘积是盲旋转的主要部分，因此使用更有效的技术来计算盲旋转中的多项式乘积将会很有益。

4、一种本身已知的在多项式环中执行有效乘法的技术是数论变换(ntt)。为了使用ntt执行多项式乘法，多项式可以用所谓的ntt傅里叶域表示来表示。通常，多项式的傅里叶域表示包括多项式在多个相应估值点中的多个相应估值。当采用傅里叶域表示时，多项式可以高效地相乘，例如，通过估值的逐点乘法。此外，使用ntt，可以从多项式的系数表示来有效地计算其傅里叶域表示(通过应用数论变换本身)，并从傅里叶域表示来有效地计算系数表示(使用逆数论变换)。多种数论变换本身都是已知的，包括离散傅里叶变换(以其标准形式定义为商多项式xn-1以及质数幂模数q，其中n|q-1)，例如在j.von zur gathen和j.gerhard的“modern computer algebra”，剑桥大学出版社，第3版，2013年，第8章(就dft的描述而言，通过引用纳入本文)中公开的，算法和nussbaumer算法，例如在d.j.bernstein的“multidigit multiplication for mathematicians”，未发表的手稿(可在https://cr.yp.to/papers.html#m3获得)，2001年8月(就和nussbaumer算法的描述而言，通过引用纳入本文)中公开的。

5、因此，“使用数论变换”执行多项式乘法通常可以指在数论变换的傅里叶域中执行多项式乘法，可选地结合使用ntt和/或其逆从该傅里叶域表示转换多项式或将多项式转换为该傅里叶域表示。

6、不幸的是，现有技术的盲旋转本身无法通过应用数论变换变得更加有效。出于效率原因，现有技术采用模数q＝2ω，例如q＝232或q＝264。同时，使用商多项式xn+1，因为这意味着关系xk＝-xk+n在多项式环中成立，这对于使现有技术的盲旋转起作用是必要的。然而，对于这些参数，应用数论变换是不可能的，因为数论变换需要xn+1除以多项式xm-1，其中m与q互质。在现有技术所采用的参数中，n和q都是2的幂，因此n的任何倍数都不可能与q互质。

7、此外，使用现有技术，不可能通过简单地改变所使用的多项式环的参数来充分受益于由数论变换所提供的改进的性能。如上所讨论的，由于关系xk＝-xk+n，因此需要商多项式xn+1。模数q＝2ω可以实现有效的模块化运算。

8、有趣的是，发明人找到了一种使盲旋转与数论变换兼容的方法。发明人意识到，没有必要依赖关系xk＝-xk+n来使与测试多项式的乘法起作用。相反，给定特定的模数以及特定的商多项式，就可以定义测试多项式，使得测试多项式与某个明文值的自举单项式的乘积将该明文值的期望输出值作为固定系数。在这种情况下，测试多项式的每个相应系数不再像现有技术中的情况那样对应于相应期望输出值，例如，测试多项式不同于尽管如此，在盲旋转中使用这样的测试多项式可以产生加密多项式，通过提取固定系数可以从中提取期望输出值。

9、利用该改进的测试多项式，可以在应用数论变换的多项式环中进行盲旋转。具体而言，多项式环可以由模数q(其例如可以是2的幂)定义并且由商多项式p(x)(例如，不同于xn+1)定义。这里，商多项式可以除以ntt多项式(即允许按模数q取模的数论变换的多项式)。通常，这意味着ntt多项式等于xm-1，其中m与q互质。给定这样的模数以及这样的商多项式，按商多项式取模的多项式乘法可以被实施为数论变换的傅里叶域中的多项式乘法，例如，作为按ntt多项式取模的多项式乘法。实际上，计算按ntt多项式取模的多项式乘法并将按商多项式取模的结果约化可以给出与执行按商多项式取模的乘法相同的结果，例如，a(x)b(x)mod p(x)＝(a(x)b(x)mod(xm-1))mod p(x)。

10、因此，可以按模q取模以及按除以ntt多项式的商多项式p(x)取模来执行盲旋转，因此，可以使用数论变换来实施盲旋转的多项式乘法。这样，与已知的盲旋转相比，盲旋转的效率得到了提高。此外，由于按模数以及商多项式取模的多项式乘法也可以出现在加密计算的其他运算中，例如，在可以作为可编程自举的一部分可选地执行的密钥切换中，这些其他运算也可以使用数论变换，因此也可以变得更加有效。

11、在一个实施方案中，模数是2的幂，例如，模数可以等于232、264或2128。因此，可以在环上执行计算，其中q是2的幂。例如，使用cpu的本机指令，此类模数可允许特别有效地实施模运算(例如，加法和/或乘法)。2的幂模数是模数的一个特定实施例，对于该模数，已知的盲旋转无法使用数论变换实施按商多项式xn+1取模，因为xm-1＝(xn+1)(xn-1)的阶数为偶数，因此不与q互质。通过使用不同的商多项式，例如xn+xn/2+1与本文所描述的测试多项式结合，有趣的是，ntt可以与这样的q一起使用。

12、在一个实施方案中，对于整数m，ntt多项式等于xm-1。例如，m可以是2的幂，或者是2的幂和/或3的幂的乘积。对于这样的m值，有效的数论变换是已知的。商多项式p(x)可能不等于xn+1，n＝m/2。在这种情况下，关系xk＝-xk+n不成立，但有利的是，使用如本文所描述的测试多项式仍然允许使用ntt。例如，商多项式p(x)可以是不等于xn+1的分圆多项式，但也可以使用不等于分圆多项式的商多项式。

13、在一个实施方案中，商多项式的阶数n严格大于ntt多项式阶数m的一半。例如，商多项式可以等于xn+xn/2+1或xn-xn/2+1，其中ntt多项式等于xm-1，m＝3n/2。这是特别有利的，因为它允许盲旋转以及因此也允许可以成为更广泛的明文值的一部分或对更广泛的明文值起作用的可编程自举。

14、具体来说，应用盲旋转的密文通常以ntt多项式的阶数m取模来定义，例如，明文可以取m个可能的值。例如，可以通过盲旋转获得密文，在所述盲旋转中将输入密文缩放到ntt多项式的阶数m。盲旋转可以能够为这些m个可能值中的n个提供期望输出值。这是因为盲旋转是基于按商多项式取模的多项式乘法，而商多项式的阶数为n。例如，在现有技术中，m＝2n，并且盲旋转通常假设输入明文的最高有效位未被设定。

15、通过选择严格大于m/2的阶数n，可以通过盲旋转来编程出大于一半的明文的比例。例如，商多项式xn±xn/2+1(例如，其中n是3的幂的两倍或3的幂的四倍)允许将可编程密文的比例从一半增加到三分之二。因此，盲旋转以及可编程自举可以对更广泛的输入密文起作用。例如，可以避免在加密计算中需要确保输入明文的最高有效位未被置位所需的额外运算，从而使加密计算更加有效。

16、在一个实施方案中，ntt多项式的阶数是2的幂和/或3的幂的乘积。在这种情况下，数论变换特别有效，因此使用它特别有利。例如，ntt多项式的阶数可以是2的幂。这个特别有效。ntt多项式的阶数也可以是3的幂，这是有利的，因为商多项式p(x)的阶数可以设定为ntt多项式的阶数的三分之二，例如p(x)＝xn+xn/2+1除以ntt多项式x3n/2-1，从而允许对很大比例的明文值进行编程。

17、在一个实施方案中，模数q为质数，并且ntt多项式的阶数m除以模数减一。在这种情况下，按模数q取模的整数域包含m次本原单位根，从而允许使用特别有效的ntt技术(诸如离散傅里叶变换)。取决于模数q，模运算也可以有效地实施，例如，按模数231<q＝10·318+1<232或263<q＝4·339+1<264取模的计算可以使用32位、64位和/或128位运算相对有效地实现，并且由于它们与常见的数据类型匹配，所以是方便的。

18、在一个实施方案中，商多项式等于xn+xn/2+1或xn-xn/2+1。正如其他地方所讨论的，商多项式的这种选择是有利，因为它允许对相对大比例的明文值进行编程。此外，对于商多项式的这种选择，可以特别有效地确定给定一组期望输出值的测试多项式。具体地，如本文所描述的，测试多项式的每个系数可以根据最多两个期望输出值来计算，具体地，作为两个期望输出值可能为负的总和。此外，有趣的是，可以以任意固定系数对期望输出值进行有效编程，例如，该系数可以不同于首项系数以及常数系数。这对于加密计算的进一步运算是有益的，其中在提取系数之前对从盲旋转所产生的加密多项式应用进一步运算。

19、可以基于定义相应明文值的期望输出值的查找表来确定测试多项式。发明人意识到，给定模数、商多项式p(x)以及ntt多项式，通常可以为给定的查找表确定合适的测试多项式。具体地，发明人意识到，对于m，商多项式p(x)除以xm-1，多项式x的逆x-1存在于r[x]/(p(x))中，并且可以表示为阶数<n且系数在r中的多项式。这使得对于给定的多项式能够推导出以下关系：xi作为r[x]/(p(x))的元素。这里，vn＝0。实际上，将测试多项式v(x)乘以单项式x-1从而会对应于将v(x)的常数项的缩放型式添加到其他系数并进行移位。基于这种关系，可以获得测试多项式与表示明文值的单项式的加密多项式乘积的表达式，作为盲旋转的一部分。从可以获得这样的表达式的事实来看，由此可以确定具有针对相应明文值的期望输出值的测试多项式。本文给出了详细的实施例，特别是对于固定系数为常数系数或首项系数的情况，以及对于商多项式等于xn+xn/2+1或xn-xn/2+1的情况。在这些情况下，测试多项式可以特别有效地计算。

20、在一个实施方案中，固定系数是常数系数或首项系数。在这种情况下，可以通过从相应期望输出值计算测试多项式的相应系数来特别有效地确定给定查找表的测试多项式，例如，测试多项式的系数可以被计算为(1)或(2)其中vi是明文值i的系数，pk是商多项式的第k个系数，并且kj是明文值j的期望输出值。

21、在一个实施方案中，应用盲旋转的密文可以是lwe类型密文。例如，盲旋转可以是对lwe类型密文执行的加密计算的一部分(例如，不涉及任何ntru类型密文)。或者，lwe类型密文可以通过从ntru类型密文转换获得，例如，作为对ntru类型密文执行的加密计算的一部分。也可以直接将盲旋转应用于ntru类型密文，而无需转换为lwe。更一般地，密文可以是格类型密文，其安全性取决于格问题的密码难度，lwe和ntru是两个实施例。

22、在一个实施方案中，执行盲旋转可以包括计算密文与小工具密文的一个或多个外积。这样的小工具密文可以包括基于小工具矩阵所定义的多个组成密文。在lwe/glwe的设置中，小工具密文可以是ggsw类型的密文。在ntru设置中，小工具加密也称为ngs加密或小工具ntru。小工具密文可以包含在自举密钥中，例如，可以表示数字，诸如用于解密应用盲旋转的密文的解密密钥的位。这种外积的计算通常涉及按模数以及商多项式取模的大量多项式乘法。通过使用所提供的技术，可以使用数论变换来执行这些多项式乘法，从而显著提有效率。

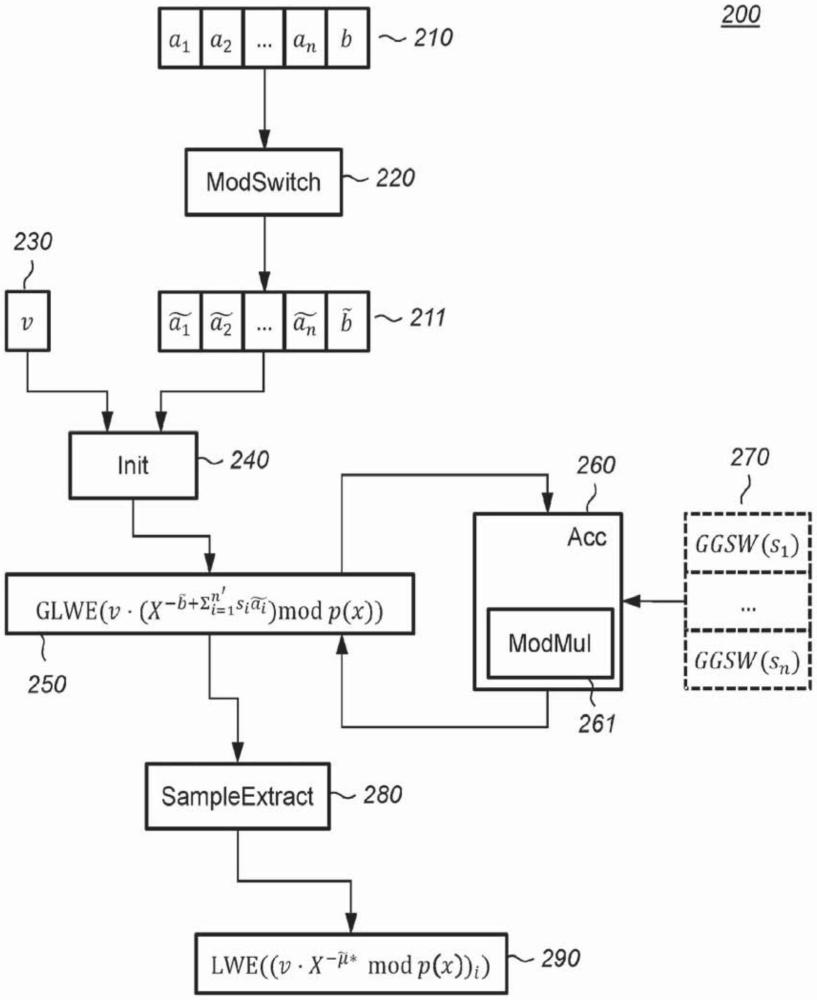
23、在一个实施方案中，加密计算方法可以包括执行可编程自举。可以对输入密文应用模数切换以获得进一步的密文，例如lwe类型密文。如本身已知，这可能涉及将输入密文缩放到ntt多项式的阶数。可以对该进一步的密文进行盲旋转。盲旋转之后可以进行样本提取，其中从通过盲旋转所计算出的多项式乘积中提取固定系数的加密。样本提取之后可以可选地进行密钥切换。具体地，该加密计算方法可以是“tfhe类”的加密计算方法，其中可编程自举是其核心运算。改进此所涉及的盲旋转可在此设置中提供重要的效率改善。

24、一般来说，可编程自举的各个步骤之间可以进行附加运算，例如，可以将若干个模数交换的密文相加在一起；在执行样本提取之前可以将若干个盲旋转的输出相加；等等。各种这样的运算可能涉及多项式乘法，例如，按商多项式取模或按除以ntt多项式的其他多项式取模。具体地，盲旋转的输出可以包括按商多项式取模的多项式，在执行样本提取之前可以对所述商多项式应用附加多项式乘法。在这种情况下，使用本文所描述的盲旋转还允许ntt用于此类附加多项式乘法，从而进一步提高可编程自举的效率。

25、在一个实施方案中，当使用数论变换执行盲旋转时，可以使用自举密钥的多项式，该多项式不是以系数表示获得的，而是以数论变换的傅里叶域表示获得的。然后，盲旋转不包括将自举密钥的这些多项式从系数表示转换为傅里叶域表示。例如，多项式可以从另一方接收或者从傅里叶域表示中的存储器中访问。这使得盲旋转特别有效，因为可以预先进行转换。由于自举密钥通常生成一次然后使用多次，因此在生成时确定其傅里叶域表示比在使用它时更有效。

26、加密计算可以是“tfhe类”加密计算。这种tfhe类加密计算的特征在于使用可编程的自举运算，其中加密多项式乘积由将明文值表示为指数的自举单项式以及测试多项式计算得出。换句话说，可编程自举可能涉及评估加密单项式的指数中的密文的解密。可以使用带有自举密钥的小工具密文的外积来计算该评估，例如ggsw类型密文、ngs密文或小工具ntrli密文。这样的小工具密文可以包含多个组成密文(例如，ggsw情况下的glwe类密文)，并且外积的计算可能涉及将小工具密文的相应组成密文乘以相应多项式。如本文所描述的，这种可编程自举在所接受的输入明文方面变得更加有效和/或更加灵活。

27、所提供的用于改进对加密数据的计算的技术可被应用于广泛的实际应用。此类实际应用包括在无需访问明文数据的情况下对软件程序进行加密评估。例如，人们可以评估关于医学数据的医学诊断软件，而无需实际访问医学数据。医学数据可以包括医学图像。医学图像可以包括例如通过多种获取方式所获取的多维图像数据，例如二维(2d)、三维(3d)或四维(4d)图像，所述多种获取方式诸如但不限于标准x射线成像、计算机断层扫描(ct)、磁共振成像(mri)、超声(us)、正电子发射断层扫描(pet)、单光子发射计算机断层扫描(spect)以及核医学(nm)。

28、在一个实施方案中，所提供的技术可用于评估关于加密输入的神经网络。评估神经网络的一方可能会或可能不会以明文方式访问神经网络的训练参数，例如权重和偏差。总体上，本文所提供的技术(例如，改进的多项式乘法、可编程自举以及外积)提高了评估神经网络的效率和/或减少了所用密文或密钥材料的存储和传输要求。

29、本方法的一个实施方案可作为计算机实施的方法而在计算机上被实施，或者在专用硬件中实施，或者在这二者的组合中实施。用于该方法的一个实施方案的可执行代码可被存储在计算机程序产品上。计算机程序产品的实施例包括内存设备、光学存储设备、集成电路、服务器、在线软件等。优选地，计算机程序产品包括存储在计算机可读介质上的非暂时性程序代码，用于当所述程序产品在计算机上执行时执行该方法的一个实施方案。

30、在一个实施方案中，该计算机程序包括计算机程序代码，当计算机程序在计算机上运行时，该计算机程序代码适于执行该方法的一个实施方案的全部或部分步骤。优选地，该计算机程序被实施在计算机可读介质上。