基于运动伪装的三方微分博弈的防御制导方法及系统

本发明属于飞行器制导方法，具体涉及基于运动伪装的三方微分博弈的防御制导方法及系统。

背景技术：

1、多人追逃微分博弈是解决多智能体系统协同控制背景下运动策略挑战的重要工具。追逃博弈的一个更实际的应用是目标-攻击者-防御飞行器(target-attack-defender,tad)三方微分博弈，其中攻击者的目标是捕获目标，而防御飞行器的目标是捕获攻击者以保护目标，而目标则努力逃避攻击者。在实际场景中，这样类似的场景经常出现在防御措施的部署中，例如发射武器以保护飞机免受来袭导弹的攻击或保护重要资产免受潜在破坏。

2、而基于微分博弈的三方博弈方法，给出的鞍点策略，在对抗更智能的追捕飞行器时能够达到更好的性能。此外，在传统的tad三体博弈中，防御飞行器的目标仅仅为捕获追捕飞行器，因此所设计的机动策略类似于追捕飞行器的捕获策略，也就是说如果需要保证可捕获性，防御飞行器的机动能力要比追捕飞行器强，这对防御飞行器的速度与过载需求过高。

3、因此，设计一种能够降低对防御飞行器性能需求，能够应用于小无人机等较低性能防御飞行器的基于运动伪装的三方微分博弈的防御制导方法及系统，就显得十分重要。

技术实现思路

1、本发明是为了克服现有技术中，在传统的tad三体博弈中，由于防御飞行器的目标仅仅为捕获追捕飞行器，需要防御飞行器的机动能力比追捕飞行器强，进而对防御飞行器的速度与过载需求过高的问题，提供了一种能够降低对防御飞行器性能需求，能够应用于小无人机等较低性能防御飞行器的基于运动伪装的三方微分博弈的防御制导方法及系统。

2、为了达到上述发明目的，本发明采用以下技术方案：

3、基于运动伪装的三方微分博弈的防御制导方法，包括如下步骤：

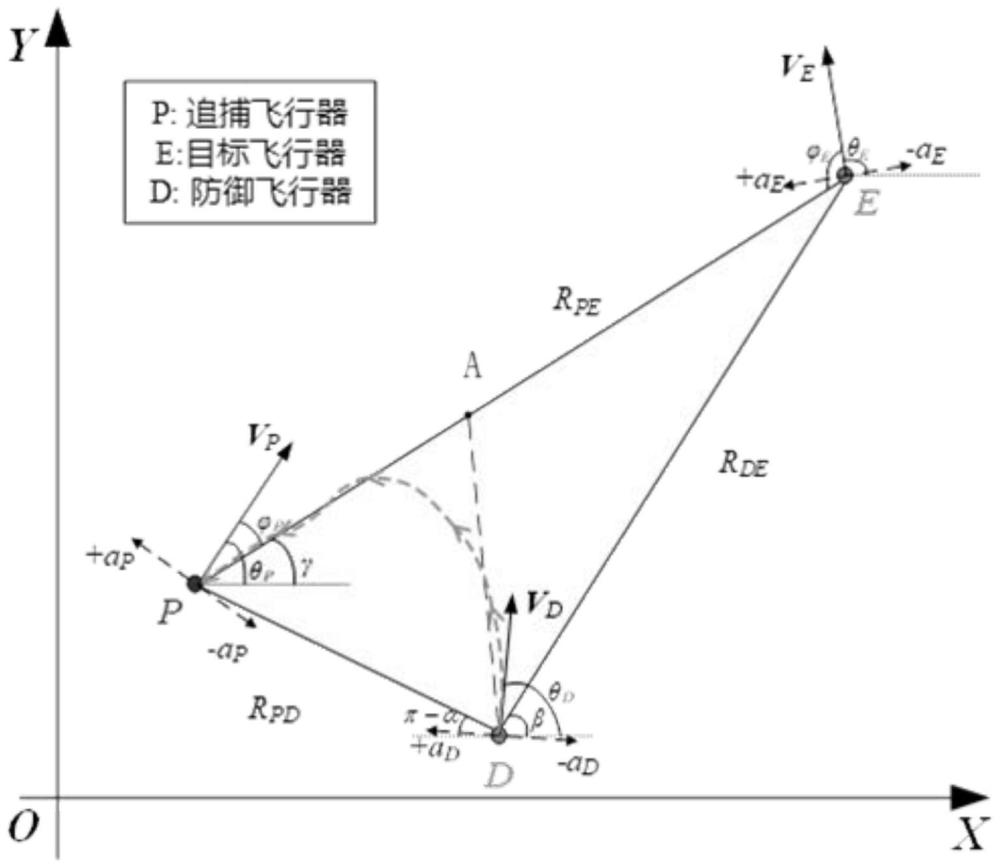
4、s1，建立三方博弈坐标系；所述三方包括追捕飞行器p、目标飞行器e和防御飞行器d；

5、s2，根据三方博弈坐标系，推导每个参与方的机动策略，以及对应所需的航向角度；

6、s3，根据步骤s2推导出的结果以及步骤s1中三方博弈的初始条件，分析追捕飞行器和防御飞行器的可捕获性。

7、作为优选，步骤s1包括如下步骤：

8、s11，设定三方博弈中每个飞行器的运动模型用如下方程表示：

9、

10、其中，xi＝[xi,yi,vxi,vyi]t，表示飞行器的运动学方程；xi,yi表示飞行器在交战平面的坐标位置，vxi,vyi表示飞行器的速度向量，θi∈[-π,π]表示瞬时航向角，具体表示为：

11、

12、其中vi为各飞行器的速度值，ai为各飞行器的转向过载，aim为飞行器转向过载上限，且|ai|≤aim；ai的符号表示各飞行器的机动方向，ai＞0为顺时针机动，ai＜0表示逆时针机动；每个飞行器的转弯半径和角速度分别表示为ri＝vi2/aim和ωi＝aim/vi；

13、s12，设定rpd、rpe和rde分别为每个飞行器之间的距离；α和β分别是x轴正方向与和方向的夹角；γ表示x轴正方向和之间的夹角；φp和φe分别是追捕飞行器p、目标飞行器e的视线方向和速度矢量之间的夹角；∠pde的角平分线记为da，a为角平分线与追捕飞行器p、目标飞行器e的视线的交点；dp＝rpd，de＝rde，分别表示空间上飞行器之间的距离；ap，ae分别飞行器与a点的距离；根据角平分线的性质，成立以下条件：

14、

15、其中，μ为一个无量纲比例参数；

16、基于运动方程(1.1)，系统的状态转移矩阵用如下形式表示：

17、

18、其中，φ(t,t+δt)为零输入状态转移矩阵；定义三方博弈的终端时间tf为追踪者捕获目标飞行器的时刻，根据los方向的相对速度来估计终端时间tf：

19、

20、vp，ve分别表示速度追捕飞行器和目标飞行器的速度向量，pe为由追捕飞行器指向目标飞行器的向量。

21、作为优选，步骤s2包括如下步骤：

22、s21，定义追捕飞行器和目标飞行器的收益函数为jpe：

23、

24、表示对于目标飞行器则寻求一个策略来最大化收益，追捕飞行器需要寻求一个策略最小化收益；

25、将状态向量和动力学写成相对形式，即

26、

27、

28、其中xp(t)和xe(t)为追捕飞行器和目标飞行器双方的状态向量；xp和yp表示追捕飞行器的位置坐标；和表示追捕飞行器的速度；xe和ye表示目标飞行器的位置坐标；和表示追捕飞行器的速度；ap和ae表示追捕飞行器和目标飞行器的机动过载值；θp和θe为追捕飞行器和目标飞行器的航向角；xpe(t)为追捕飞行器和目标飞行器双方的相对状态向量；fpe(t)均表示追捕飞行器和目标飞行器双方的相对动力学模型；

29、最终得到对应博弈的哈密顿函数hpe为

30、

31、其中，λpe＝[λ1,λ2,λ3,λ4]t为协态变量向量，λ1～λ4为协态变量；

32、根据追逃博弈公式(1.6)和相对动态博弈公式(1.7)和(1.8)，得出追捕飞行器和目标飞行器的机动策略如下：

33、

34、其中，p1＝xpf-xef,p2＝ypf-yef；

35、为双方的最优策略向量；分别表示追捕飞行器与目标飞行器的最优策略；apm与aem分别为追捕飞行器与目标飞行器的转向过载上限；xpf，ypf表示追捕飞行器的终端位置；xef，yef表示目标飞行器的终端位置。

36、作为优选，步骤s2还包括如下步骤：

37、s22，定义追捕飞行器和防御飞行器的收益函数jpd为：

38、

39、表示对于追捕飞行器则寻求一个策略来最大化收益，防御飞行器需要寻求一个策略最小化收益；

40、将相对状态、相对运动方程和协态变量写成如下形式：

41、

42、其中xp(t)、xd(t)分别为追捕飞行器和防御飞行器的状态向量；xpd(t)为相对状态向量形式；fpd则为相对动力学形式；λpd为协态变量向量，λ5～λ8则为相应的协态变量；

43、得到对应的哈密顿方程hpd为：

44、

45、基于博弈公式(1.11)和相对动态公式(1.12)，确定防御飞行器的机动策略为：

46、

47、其中

48、其中xd，yd为防御飞行器的坐标位置；为防御飞行器的最优策略；adm为防御飞行器的过载上限；θd为防御飞行器的航向角。

49、作为优选，步骤s2还包括如下步骤：

50、s23，在追逃博弈中，对于追击者来说，最优的捕获策略为平行策略，即追捕飞行器和目标飞行器只有在los方向上才有相对速度，即满足

51、

52、其中vp和ve分别为追捕飞行器和目标飞行器的速度值；在已知追捕飞行器和目标飞行器的速度和方向角的情况下，获得追捕飞行器和目标飞行器之间的接近速度和沿los垂直方向的速度vl，即

53、

54、

55、和分别为追捕飞行器和目标飞行器的最优航向角。

56、作为优选，，步骤s2还包括如下步骤：

57、s24，根据式(1.13)中防御飞行器的机动策略，推导出防御飞行器的航向角为：

58、

59、其中为防御飞行器的目标航向角。

60、作为优选，步骤s3包括如下步骤：

61、s31，追捕飞行器捕获目标飞行器条件分析：

62、为了保证追捕飞行器在有限的时间内捕获目标飞行器，设定满足以下条件：

63、vp＞ve,rp＜re(1.19)；

64、其中，条件vp＞ve确保整个策略空间在追捕飞行器的捕获域内；条件rp＜re表示追捕飞行器的转弯半径小于目标飞行器的转弯半径，使得在双方相对位置接近时，目标飞行器无法通过持续机动转弯的方式逃脱。

65、作为优选，步骤s3还包括如下步骤：

66、s32，防御飞行器的捕获条件分析：

67、基于推导出的机动策略公式(1.10)和(1.13)及对应的几何含义公式(1.14)和(1.18)，对博弈结束时间tf的精确估计表示为：

68、

69、其中和分别为追捕飞行器和目标飞行器的最优航向角，表示为：

70、

71、和分别代表初始时刻追捕飞行器和目标飞行器航向和视线方向的夹角；和表示追捕飞行器和目标飞行器最优机动值；ts表示追捕飞行器和目标飞行器在初始阶段的机动时间，具体表示为：

72、

73、由于设定防御飞行器的初速度矢量表示为vd[cosθd0,sinθd0]t，则求解捕获区域相当于找到防御飞行器的速度值vd和初始航向角θd0的边界；

74、设定防御飞行器赢得比赛的充分条件表示为：

75、

76、式中，ωd＝adm/vd为防御飞行器的最大角速度；为防御飞行器的转向半径；为防御飞行器的最优航向角；γ表示追捕飞行器和目标飞行器视线与x轴正方向夹角；va＝|va|，va表示a点处的速度矢量，表达式为：

77、

78、其中vp和ve分别代表追捕飞行器和目标飞行器的速度矢量。

79、本发明还提供了基于运动伪装的三方微分博弈的防御制导系统包括：

80、模型建立模块，用于建立三方博弈坐标系；所述三方包括追捕飞行器p、目标飞行器e和防御飞行器d；

81、机动策略推导模块，用于根据三方博弈坐标系，推导每个参与方的机动策略，以及对应所需的航向角度；

82、可捕获性分析模块，用于根据机动策略推导模块推导出的结果以及三方博弈的初始条件，分析追捕飞行器和防御飞行器的可捕获性。

83、本发明与现有技术相比，有益效果是：(1)本发明建立了三体博弈对抗模型，结合运动伪装理论，主要设计了防御飞行器的掩护策略；不同于以直接捕获追捕飞行器为目标的传统的防御制导方法，该策略下，防御飞行器以目标飞行器与追捕飞行器的视线为目标，通过使自身在两方视线上移动来掩护目标飞行器；(2)相比于传统的三体博弈中对防御飞行器的机动策略设计，本发明方法降低了对防御飞行器的过载的需求；并且所设计的策略为解析形式，因此可以应用于小无人机等较低性能的防御飞行器中；(3)本发明由于机动策略并非以拦截追逐飞行器为主要目标，属于是一种非自杀式的防御策略，因此未来有望用于可回收类型的智能飞行器或低成本卫星的追逃博弈、空间轨道博弈场景。