基于曲率自适应调节曲率线疏密的曲板曲率线展开法及其应用

本发明属于复杂形状曲板成形相关，更具体地，涉及一种基于曲率自适应调节曲率线疏密的曲板曲率线展开法及其应用。

背景技术：

1、船舶、航空、汽车和建筑等领域存在大量三维复杂形状曲板成型需求。对于薄板而言，将薄板曲面展开后采用折弯、冲压、拉深等钣金工艺即可成型。而对于一般中厚板，如船舶曲板，采用曲率线展开法将其展开，再使用线加载成型工艺成型。对于复杂形状中厚曲板，其曲面上两族曲率线构成曲率线网，将法曲率积分均值较大的一族曲率线称为第一族曲率线，将法曲率积分均值较小的另一族曲率线称为第二族曲率线。使用曲率线展开法，将这两族曲率线保长保持正交地展开到平面，从而得到曲板的展开平板。两族曲率线展开后，第一族曲率线法曲率变化量及第二族曲率线收缩量即曲板成型所需的弯曲量和收缩量。由于两族曲率线及其展开线的正交性，沿第二族曲率线的展开线进行线冷弯加工，板在第一族曲率线展开线方向弯曲，然后沿第一族曲率线的展开线进行线加热，板在第二族曲率线展开线方向收缩与弯曲，使得曲板成型。

2、由于展开的曲率线作为线加载的加工路径，同时，展开过程两族曲率线的法曲率变化量和收缩量是曲板线加载成型加工中沿加工路径所需的弯曲量和收缩量。故中厚曲板的线加载成型会受曲率线的疏密情况影响。现有的曲率线展开法采用的是等间隔的曲率线网。而对于复杂形状的曲板，曲面上曲率分布不均匀，不同区域曲率值大小不等，在曲率较大的区域需要更大的弯曲量，当该区域第二族曲率线的间隔较大即较为稀疏时，其在展开中法曲率变化量即曲面所需弯曲量不足，曲板在此区域难以成型；而若对曲面进行全局曲率线加密，就会增加线加载路径从而消耗更多工时，效率较低，同时还会由于相邻线间的影响，导致可加工性变差。

技术实现思路

1、针对现有技术的以上缺陷或改进需求，本发明提供了一种基于曲率自适应调节曲率线疏密的曲板曲率线展开法及其应用，其解决了现有的等间距曲率线网导致的曲板成形效果及效率差的问题。

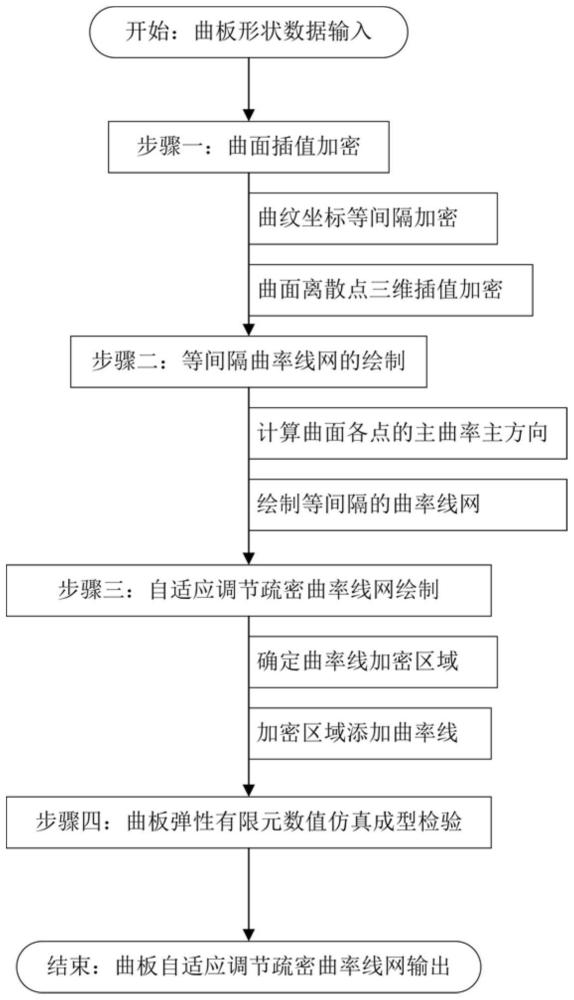
2、为实现上述目的，按照本发明的一个方面，提供了一种基于曲率自适应调节曲率线疏密的曲板曲率线展开法，该展开法包括以下步骤：

3、s1，对曲板进行预处理以得到等间距插值加密的离散曲面；

4、s2，基于等间距插值加密的离散曲面得到等间距曲率线网；

5、s3，依据曲板面上高斯曲率分布特征确定曲率待加密区域，计算待加密区域中所有曲率线法曲率积分均值的平均值，在通过该待加密区域的第二族曲率线中法曲率积分均值大于该平均值的曲率线附近添加曲率线，得到基于曲面高斯曲率和曲率线法曲率自适应调节疏密的曲率线网；

6、s4，基于得到的曲率线网对曲板曲面进行曲率线展开。

7、进一步地，采用基于三角剖分的自然邻点三维插值法对曲面离散点进行加密后，对等间隔加密的曲纹坐标网格进行关于曲面垂向坐标的插值加密，以得到等间距插值加密的离散曲面。

8、进一步地，计算等间距插值加密后曲面的第一、第二类基本量、高斯曲率和平均曲率，并求取曲面各点的主曲率以及相应的主方向；曲率线横向与纵向分别取预定间隔，然后从曲面边界按照间隔取点作为起点分别绘制曲率线，得到曲率线网。

9、进一步地，计算两族曲率线上法曲率的积分值，再求取该积分值关于弧长的均值，即两族曲率线的法曲率积分均值，数值大的为第一族曲率线，较小的为第二族曲率线。

10、进一步地，计算曲面关于曲纹坐标(u,v)的一阶偏导ru和rv、二阶偏导ruu、ruv和rvv、以及法向量并由此计算曲面的第一、第二类基本量：

11、e＝ru·ru,f＝ru·rv,g＝rv·rv

12、l＝ruu·n,m＝ruv·n,n＝rvv·n

13、再计算曲面的高斯曲率k和平均曲率h，计算式如下：

14、

15、利用两者与主曲率(κ1,κ2)的关系式：计算得到曲面各点处主曲率。

16、进一步地，曲面各点主方向(du:dv)由下式计算得到：

17、-ldu-mdv＝-ki(edu+fdv)i＝1,2

18、-mdu-ndv＝-ki(fdu+gdv)i＝1,2

19、得到曲面上各点的主曲率和主方向后，从曲面左下角点开始，向右沿着边界线，按照间隔δu取点；然后从左下角点向上沿边界线，按照间隔δv取点，取得的点分别作为两族曲率线的起点，初始间隔为

20、进一步地，依据曲板曲面到展开平面的点坐标映射关系，求取外板曲面数值仿真成型所需的应变，将得到的应变以初应力的形式加载于展开平面上，采用弹性有限元计算方法，通过曲板数值仿真成型的结果检验自适应调节疏密的曲率线网，最终输出该曲率线网。

21、进一步地，计算曲面上各点高斯曲率的绝对值|k|，进而将绝对值|k|与设定阈值进行比较，将高斯曲率绝对值|k|大于设定阈值的区域确定为曲面曲率线待加密区域。

22、进一步地，设定阈值为绝对值|k|的平均值；将通过待加密区域的第二族曲率线群记作gcl，求取gcl中各条曲率线上法曲率关于弧长的积分均值imκn，计算式如下：

23、

24、计算第二族曲率线各线法曲率积分均值imκn的平均值msum，对于gcl中法曲率积分均值imκn大于msum的曲率线，在其两侧增加an条曲率线，an计算式如下：

25、

26、本发明还提供了一种如上所述的基于曲率自适应调节曲率线疏密的曲板曲率线展开法在曲板成形中的应用。

27、总体而言，通过本发明所构思的以上技术方案与现有技术相比，本发明提供的基于曲率自适应调节曲率线疏密的曲板曲率线展开法及其应用主要具有以下有益效果：

28、1.本发明在曲板高斯曲率较大的区域适当加密法曲率积分均值较大的曲率线，同时保证全局曲率线不过于稠密，从而得到复杂形状中厚曲板成型展开所需的曲率线网，实现曲板成型，并提高其可加工性，进而提高了曲板的成形效率及成形质量。

29、2.工程中复杂形状曲板一般以离散数据点来表示，先进行预处理，即得到等间距插值加密的离散曲面，从而提高曲率线的绘制精度。

30、3.计算曲面上各点高斯曲率的绝对值|k|，并求取|k|的平均值m|k|，将高斯曲率绝对值|k|大于其平均值m|k|的区域确定为曲面曲率线待加密区域，如此能够准确快速的得到待加密区域，进而可以实现高效的区域加密。

技术特征：

1.一种基于曲率自适应调节曲率线疏密的曲板曲率线展开法，其特征在于，该展开法包括以下步骤：

2.如权利要求1所述的基于曲率自适应调节曲率线疏密的曲板曲率线展开法，其特征在于：采用基于三角剖分的自然邻点三维插值法对曲面离散点进行加密后，对等间隔加密的曲纹坐标网格进行关于曲面垂向坐标的插值加密，以得到等间距插值加密的离散曲面。

3.如权利要求1所述的基于曲率自适应调节曲率线疏密的曲板曲率线展开法，其特征在于：计算等间距插值加密后曲面的第一、第二类基本量、高斯曲率和平均曲率，并求取曲面各点的主曲率以及相应的主方向；曲率线横向与纵向分别取预定间隔，然后从曲面边界按照间隔取点作为起点分别绘制曲率线，得到曲率线网。

4.如权利要求3所述的基于曲率自适应调节曲率线疏密的曲板曲率线展开法，其特征在于：计算两族曲率线上法曲率的积分值，再求取该积分值关于弧长的均值，即两族曲率线的法曲率积分均值，数值大的为第一族曲率线，较小的为第二族曲率线。

5.如权利要求4所述的基于曲率自适应调节曲率线疏密的曲板曲率线展开法，其特征在于：计算曲面关于曲纹坐标(u,v)的一阶偏导ru和rv、二阶偏导ruu、ruv和rvv、以及法向量并由此计算曲面的第一、第二类基本量：

6.如权利要求5所述的基于曲率自适应调节曲率线疏密的曲板曲率线展开法，其特征在于：曲面各点主方向(du：dv)由下式计算得到：

7.如权利要求1所述的基于曲率自适应调节曲率线疏密的曲板曲率线展开法，其特征在于：依据曲板曲面到展开平面的点坐标映射关系，求取外板曲面数值仿真成型所需的应变，将得到的应变以初应力的形式加载于展开平面上，采用弹性有限元计算方法，通过曲板数值仿真成型的结果检验自适应调节疏密的曲率线网，最终输出该曲率线网。

8.如权利要求1-7任一项所述的基于曲率自适应调节曲率线疏密的曲板曲率线展开法，其特征在于：计算曲面上各点高斯曲率的绝对值|k|，进而将绝对值|k|与设定阈值进行比较，将高斯曲率绝对值|k|大于设定阈值的区域确定为曲面曲率线待加密区域。

9.如权利要求8所述的基于曲率自适应调节曲率线疏密的曲板曲率线展开法，其特征在于：设定阈值为绝对值|k|的平均值；将通过待加密区域的第二族曲率线群记作gcl，求取gcl中各条曲率线上法曲率关于弧长的积分均值imκn，计算式如下：

10.一种权利要求1-9任一项所述的基于曲率自适应调节曲率线疏密的曲板曲率线展开法在曲板成形中的应用。

技术总结本发明属于复杂形状曲板成形相关技术领域，其公开了一种基于曲率自适应调节曲率线疏密的曲板曲率线展开法及其应用,该展开法包括以下步骤：S1，对曲板进行预处理以得到等间距插值加密的离散曲面；S2，基于等间距插值加密的离散曲面得到等间距曲率线网；S3，依据曲板面上高斯曲率分布特征确定曲率待加密区域，计算待加密区域中所有曲率线法曲率积分均值的平均值，在通过该待加密区域的第二族曲率线中法曲率积分均值大于该平均值的曲率线附近添加曲率线，得到基于曲面高斯曲率和曲率线法曲率自适应调节疏密的曲率线网；S4，基于得到的曲率线网对曲板曲面进行曲率线展开。本发明解决了等间距曲率线网导致的曲板成形效果及效率差的问题。技术研发人员：赵耀,邵凯,袁华,常利春,魏振帅受保护的技术使用者：华中科技大学技术研发日：技术公布日：2024/9/9