一种路基沉降预测置信度分析方法及系统与流程

本发明涉及铁路以及路基沉降预测分析，特别涉及一种路基沉降预测置信度分析方法及系统。

背景技术：

1、铁路运输在我国总体交通网络中占据骨干地位。近年来，基于我国高速铁路的飞速发展，铁路建设和运维已经成为拉动我国国内经济增长的重要动力以及对外展示国际形象的靓丽名片。我国对铁路的中长期发展进行了规划。但由于我国是一个软土广泛分布的国家，铁路线路势必要通过大量的软土地区。软土地区修建高速铁路所面临的一个重要的问题是地基沉降及工后沉降控制问题。针对不同等级的铁路，提出了不同的沉降控制标准，高速铁路无砟轨道的高平顺性需求，对路基工后沉降提出了更为严苛的要求，一般要求工后沉降需不大于15mm，这就使建设过程中必须对路基的最终沉降量进行准确的控制。

2、然而，现有技术中仍然存在如下技术缺陷：

3、第一，现行的工程设计和施工中主要以在设计阶段进行沉降计算和在施工阶段进行路基沉降观测预测与评估以进行工后沉降控制。但由于土体应力—应变关系的非线性，岩土参数的变异性和各向异性等因素，导致了理论计算方法，尤其是设计阶段的以分层总和法为基础的理论计算方法，对地基的沉降发展过程和最终沉降量的计算偏差较大。施工阶段的路基沉降观测预测与评估是以观测数据外推沉降发展过程和最终沉降量，由于沉降观测过程中受到地基处理形式、地质条件、观测条件等众多因素的影响，且上述因素对沉降预测结果的影响规律不清，采用沉降观测预测不易进行高速铁路路基沉降控制。

4、第二，现有技术中并没有研究观测条件对沉降预测均值和标准差的影响规律的成熟的技术方案。

5、第三，沉降预测是基于现场实测数据，采用曲线拟合方法等数学手段，以外推路基的最终沉降量和工后沉降。但对于沉降预测置信度的分析，需要大量的试验数据。现场条件复杂，难以有效地准确控制地基处理形式和土性条件、观测精度、观测频次、观测时长等影响；由于土性参数的变异性和各向异性，试验室内无法得到精度的试验数据。

技术实现思路

1、本发明的目的是提供一种路基沉降预测置信度分析方法及系统，采用根据观测频次、观测时长、观测精度等观测条件，对沉降理论计算曲线通过离散、截取和叠加随机误差生成模拟沉降观测数据，开展样本的曲线拟合沉降预测与分析，研究观测条件对沉降预测均值和标准差的影响规律。

2、本发明的第一方面在于提供一种路基沉降预测置信度分析方法，包括：

3、s1，生成模拟沉降观测数据，其中所述模拟沉降观测数据基于带有观测误差的离散观测数据生成；

4、s2，确定均质天然地基条件下和均质砂井地基条件下高铁软土路基沉降预测模型适用性；

5、s3，基于所述模拟沉降观测数据、所述均质天然地基条件下和所述均质砂井地基条件下高铁软土路基沉降预测模型适用性进行路基沉降预测置信度分析。

6、优选的，所述s1包括：

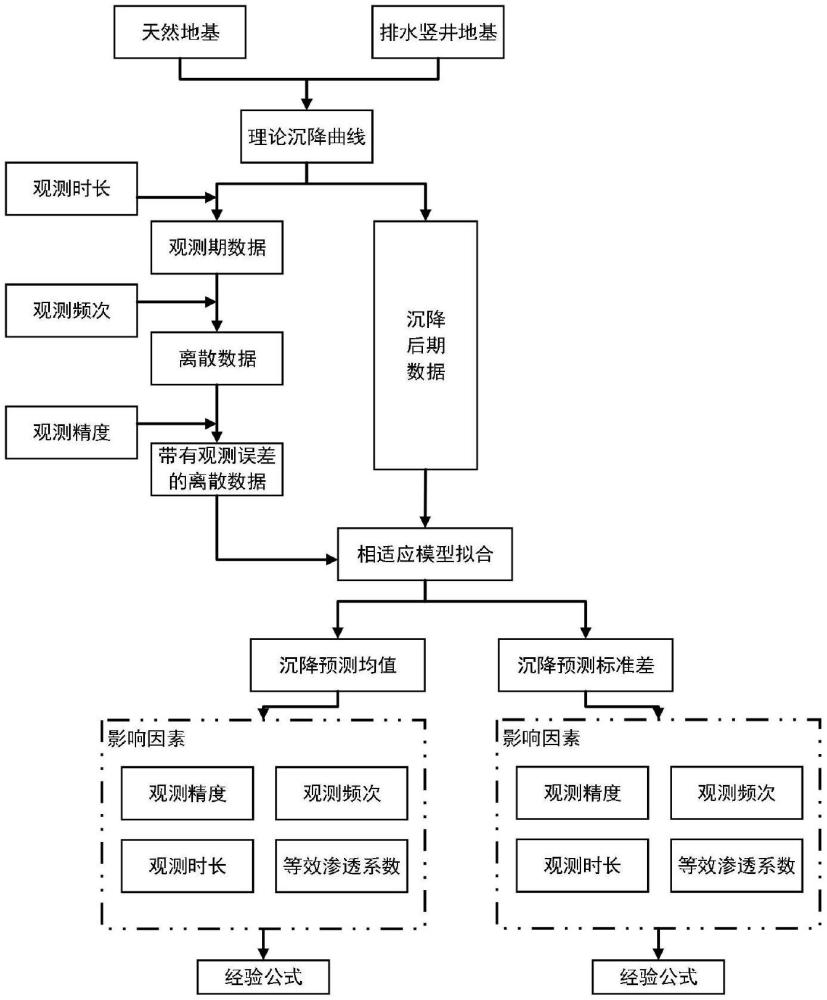
7、s11，针对不同地基处理形式和不同土性条件下的软土路基沉降问题，基于均质天然地基计算模型和砂井地基计算模型计算并获得不同条件下对应的理论连续数据；

8、s12，将所述理论连续数据按照不同的第一沉降观测条件分为观测期数据和沉降后期数据，并对所述观测期数据按照第二沉降观测条件进行离散后获得离散数据；

9、s13，按照不同的第三沉降观测条件对离散的观测期数据叠加观测误差以生成带有所述观测误差的离散观测数据，并基于带有所述观测误差的离散观测数据生成所述模拟沉降观测数据。

10、优选的，所述第一沉降观测条件为观测时长；所述第二沉降观测条件为观测频次；所述第三沉降观测条件为观测精度。

11、优选的，所述观测精度参考工程水准测量中ⅰ等水准、ⅱ等水准、ⅲ等水准、ⅳ等水准以及较ⅳ等水准观测误差更大的观测精度条件对沉降预测置信度的影响，以变形点高程中误差作为区分各级别水准测量精度的控制指标；所述观测频次是指在观测时长内采用水准观测方法观测的次数或频率；在分析观测频次对沉降预测置信度影响时，将路基填筑完成后不同恒载期划分为填筑完成后0～3个月内、填筑完成后4-6个月以及填筑完成后6个月三个观测时期，分别确定较现行相关规定中加密或减疏相应观测期内的观测频次对预测置信度的影响规律。

12、优选的，所述s2包括：

13、s21，运用均质天然地基和排水竖井地基沉降理论模型，得到不同土性、地基处理条件下沉降理论曲线；

14、s22，基于工程常用的观测条件对所述沉降理论曲线进行处理，生成模拟沉降观测数据，采用曲线拟合模型对模拟沉降观测数据展开预测；

15、s23，基于等效渗透系数方法对均质排水竖井地基的土性和结构参数进行归一化处理，综合利用沉降预测结果相关系数、相对误差和变异系数确定沉降预测模型适用性评价指标，基于所述适用性评价指标分析得到不同曲线拟合模型的最佳使用条件；

16、优选的，所述s3包括：

17、s31，基于所述带有所述观测误差的离散观测数据，运用曲线拟合方法进行预测获得每组观测数据对应的预测值；重复s31获得多个预测值组成预测结果；

18、s32，对所述预测结果进行统计学分析，获得预测沉降统计均值和预测沉降标准差；

19、s33，分别基于所述预测沉降统计均值和预测沉降标准差得出相应的影响规律。

20、优选的，所述影响规律包括观测时长对预测沉降统计均值的影响规律、观测精度对预测沉降统计均值的影响规律、观测频次对预测沉降统计均值的影响规律、土性条件对预测沉降统计均值的影响规律、观测时长对预测沉降标准差的影响规律、观测精度对预测沉降标准差的影响规律、观测频次对预测沉降标准差的影响规律以及土性条件对预测沉降标准差的影响规律。

21、本发明的第二方面还提供一种路基沉降预测置信度分析系统，用于实施第一方面的方法，包括：

22、数据生成模块(101)，用于生成模拟沉降观测数据，其中所述模拟沉降观测数据基于带有观测误差的离散观测数据生成；

23、预测模型适用性分析模块(102)，用于确定均质天然地基条件下高铁软土路基沉降预测模型适用性；

24、置信度分析模块(103)，用于基于所述模拟沉降观测数据和所述均质天然地基条件下高铁软土路基沉降预测模型适用性进行路基沉降预测置信度分析。

25、本发明的第三方面提供一种电子设备，包括处理器和存储器，所述存储器存储有多条指令，所述处理器用于读取所述指令并执行如第一方面所述的方法。

26、本发明的第四方面提供一种计算机可读存储介质，所述计算机可读存储介质存储有多条指令，所述多条指令可被处理器读取并执行如第一方面所述的方法。

27、本发明的方法和系统的有益效果：

28、(1)预测沉降统计均值随观测时长的增加而减小。二者呈指数关系，分析了预测沉降统计均值受观测时长的影响规律并获得了其相关关系。观测时长较短时，预测最终沉降量系统误差较大，预测沉降统计均值随着观测时长的延长减小幅度明显，表明预测最终沉降量的系统误差随着观测时长的增加明显减小。

29、(2)预测沉降标准差随观测时长的增加而减小。二者呈指数关系，分析了预测沉降标准差受观测时长的影响规律并获得了其相关关系。观测时长较短时，表明预测最终沉降量偶然误差偏大，预测沉降标准差随着观测时长的延长减小幅度明显，表明预测最终沉降量的偶然误差随着观测时长的增加明显减小。

30、(3)观测频次越密，相同观测时长时预测沉降统计均值越小，分析了预测沉降统计均值受观测频次的影响规律并获得了其相关关系。预测最终沉降量的系统误差越小且改变0～3个月观测频次、4～6个月观测频次、6个月后观测频次对预测沉降统计均值的影响程度依次递减。当观测时长为3个月，观测频次为分别为1次/5天、1次/1周、1次/10天时，预测沉降统计均值相对误差分别为6.89％、15.97％、

31、(4)改变0～3个月观测频次、4～6个月观测频次、6个月后观测频次对预测沉降标准差的影响规律不同，分析了预测沉降标准差受观测频次的影响规律并获得了其相关关系。加密0～3个月观测频次对偶然误差的减小无益。对观测时长为6个月时，改变4～6个月观测频次为1次/10天、1次/2周、1次20天的预测沉降标准差分别为2.85mm、4.11mm、4.45mm。

32、(5)对于大量样本重复统计，观测精度对预测沉降统计均值的影响不显著。随着观测精度的放宽，预测沉降标准差呈指数级增长，分析了预测沉降标准差受观测精度的影响规律并获得了其相关关系。采用ⅰ等水准观测预测得到预测沉降标准差为ⅱ等水准的50.7％，为ⅲ等水准的25.2％.为ⅳ等水准的8.4％，为较ⅳ等水准更宽精度的2.9％～4.6％。

33、(6)分析获得了预测沉降统计均值和标准差随观测条件的影响规律，建立了不同拟合曲线、不同软土地基条件预测沉降统计均值和标准差随观测精度、观测时长、观测周期的经验公式。