基于自导向在线学习与高效率采样的机床结构优化方法

本发明涉及了一种机床结构优化方法，涉及结构设计相关，具体涉及一种基于自导向在线学习与高效率采样的机床结构优化方法。

背景技术：

1、拓扑优化是一种在设计域内推导生成满足给定负载和边界条件下的最优设计的方法。在拓扑优化中，物体被表示为一个连续的材料分布模型，而不是传统的离散实体。这种方法利用计算机算法和数学优化技术，自动探索并寻找最优的材料分布，以最大程度地提高设计目标并减少不必要的材料使用。

2、目前，拓扑优化方法可以大致分为两类：一类是以变密度法和渐进优化法为代表的密度描述模型，另一类是以水平集法和移动可变形组件法为代表的边界描述模型。其中，变密度法由于其数学模型直观、实现方式简单且计算高效的优势，应用最为广泛。尽管拓扑优化具有概念设计的优势，但大多都基于有限元分析，而计算过程中的一系列设计变量使得其应用受限于计算成本。

3、人工智能包括计算机模拟人类行为的系统技术，机器学习是人工智能的子集，旨在通过统计方法从数据中学习有意义的模式。深度学习是机器学习的子集，寻求通过从数据本身训练多层神经网络结构的方法来提高学习能力。通过将深度学习技术与传统拓扑优化方法相结合，可以实现更高效、更准确的材料分布预测和结构优化。深度学习模型能够从大量历史数据和拓扑优化结果中学习，提取隐藏的特征和规律，从而加速优化过程、降低计算成本，并生成更复杂、更优化的拓扑结构，使得工程设计得到更加创新和优化。目前应用在拓扑优化领域的深度学习算法可以分为有监督学习、无监督学习、半监督学习和强化学习四大类。神经网络属于其中的有监督学习。利用深度学习以改进拓扑优化技术的研究目的包括加速迭代、实现非迭代优化、元建模、设计空间的降维、优化器的改进、生成式设计和后处理。

4、虽然各类深度学习方法已经在大量试验中验证了在拓扑优化问题中的适用性，但在计算过程中其也暴露出了一些局限性。首先，目前大部分结合深度学习的拓扑优化方法不具有拓展性，即一种方法在二维与三维间并没有可转换性，而在现实的大规模问题中，必须应用三维设计领域。其次，在拓扑优化领域应用深度学习方法时，应当考虑数据采集成本和模型训练效率。第三，由于物理信息没有得到正确的反映，优化结果是用像素间的相似度来预测，因此优化结果的连通性可能无法得到保证。第四，用于拓扑优化的神经网络是否具备鲁棒性还有待验证和改进，评价指标需要进一步完善。最后，计算成本和精度通常是一种权衡关系，虽然深度学习的目标是加速，但精度仍不如传统的拓扑优化方法，而在中间过程中使用有限元分析提高精度的方法，依旧会带来计算成本高和时长增加的问题。

技术实现思路

1、为了解决背景技术中存在的问题，本发明所提供一种基于自导向在线学习与高效率采样的机床结构优化方法。本发明方法利用自导向在线机器学习的方法，通过在卷积层的权重参数中添加概率分布关系，搭建出深度神经网络。利用深度神经网络进行案例拓扑优化过程的学习，根据设定好的目标函数与边界条件逐步调整样本点的生成范围，在高效率采样过程中实现对拓扑优化的自导向学习。

2、本发明采用的技术方案是：

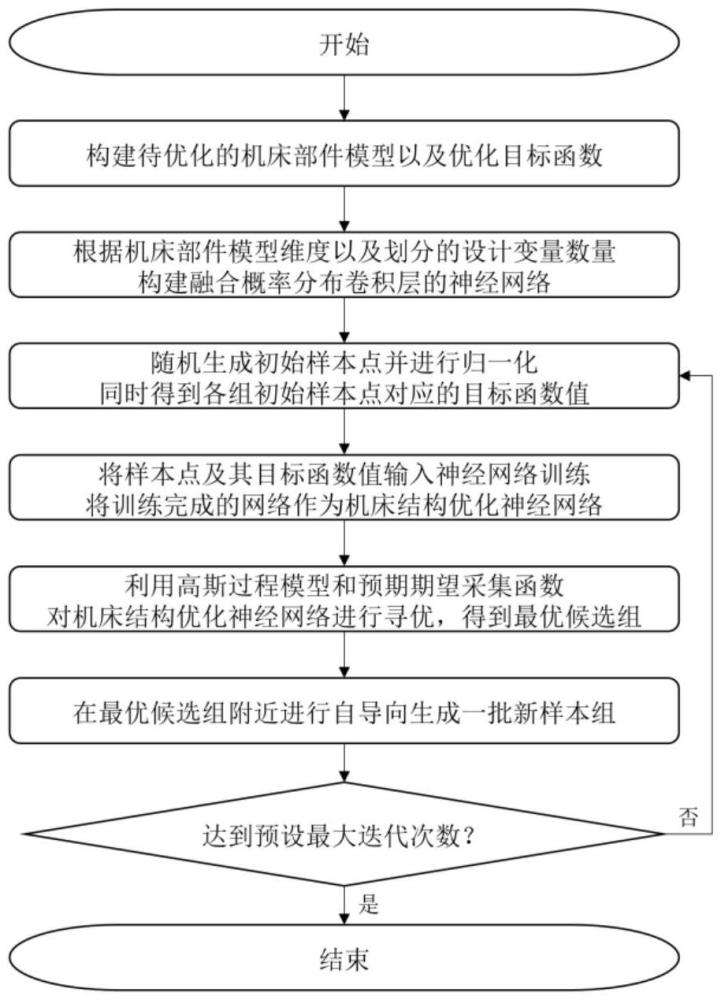
3、本发明的基于自导向在线学习与高效率采样的机床结构优化方法，包括：

4、1)构建待优化的机床部件的二维/三维模型以及基于材料体积约束的优化目标函数；关键机床部件主要包括立柱、主轴和床身。

5、2)构建融合概率分布卷积层的神经网络，融合概率分布卷积层的神经网络的输入维度根据机床部件的二维/三维模型的维度及其设计变量的数量确定，同时构建融合概率分布卷积层的神经网络的包括信息散度值的损失函数。

6、3)随机生成机床部件的二维/三维模型中的各个设计变量的若干组初始样本点并进行归一化处理后获得若干组初始样本组，将各组初始样本组输入优化目标函数中获得每组初始样本组的目标函数值。

7、4)将各组初始样本组及其目标函数值输入融合概率分布卷积层的神经网络中进行训练，直至损失函数收敛后获得训练完成的融合概率分布卷积层的神经网络作为机床结构优化神经网络。

8、5)利用高斯过程模型和预期期望采集函数对机床结构优化神经网络进行寻优，获得各个设计变量的最优候选点组成最优候选组，在最优候选组附近进行自导向生成一批新样本组。

9、6)将最优候选组和新样本组重复步骤3)-6)中初始样本组的相同的操作，从而对机床结构优化神经网络进行迭代训练，直至达到预设最大迭代次数则停止迭代训练，获得此时的各个设计变量的最优候选点作为机床部件的设计变量的最优解，从而进行机床结构的设计，实现机床结构优化。

10、所述的步骤1)中，二维/三维模型中，待优化的机床部件的结构所在的区域为设计域，设计域中离散化为若干有限元节点，各个有限元节点处的设计变量为密度值，密度值取1或0。

11、所述的步骤1)中，基于材料体积约束的优化目标函数具体如下：

12、

13、其中，ρ为各个有限元节点的密度值集合，ρ1,ρ2,…,ρi,…,ρn分别为第1、2、…、i、…、n个有限元节点的密度值；f(ρ)为各个有限元节点的密度值集合ρ的目标函数值；为各个有限元节点的密度值集合ρ下的机床部件的结构柔度，在单固体力学场作用下，目标函数一般定为结构柔度；g0(ρ)为各个有限元节点的密度值集合ρ下的机床部件的材料体积约束，wi为第i个有限元节点的密度值占整体体积积分的权重，v0为机床部件的预设体积阈值；优化目标函数中的除了材料体积约束的其他可能的约束均小于等于零；s为各个有限元节点的密度值的取值范围，s＝[0,1]。

14、所述的步骤2)中，融合概率分布卷积层的神经网络包括依次连接的m个第一块结构和一个第二块结构，第一块结构包括依次连接的概率分布卷积层、批量归一化层和softplus激活函数，第二块结构包括依次连接的全连接层和概率分布线性层；融合概率分布卷积层的神经网络的输入为各个有限元节点处的密度值集合ρ，融合概率分布卷积层的神经网络的输出包括各个有限元节点处的密度值集合ρ的目标函数均值f(ρ)_a、目标函数标准差f(ρ)_δ以及信息散度值kl。

15、所述的概率分布卷积层具体如下：

16、

17、其中，bj为融合概率分布卷积层的神经网络中的第j个第一块结构中的概率分布卷积层的输出；ak为输入融合概率分布卷积层的神经网络中的第k组初始样本组的感受野，*为卷积运算，μk为第k组初始样本组中的均值；εj为第j个第一块结构中的概率分布卷积层的方差权重参数，εj服从(0，1)的正态分布，αk为输入融合概率分布卷积层的神经网络中的第k组初始样本组的方差的组成参数，⊙为分量乘法运算。

18、所述的步骤2)中，融合概率分布卷积层的神经网络的输入总共包括四个维度，第一维的取值为输入融合概率分布卷积层的神经网络的初始样本组的组数，当待优化的机床部件构建的模型为二维模型时，第二维的取值为1，第三维和第四维的取值分别为二维模型中在长宽维度上的设计变量的数量，维度乘积与设计变量总数一致；当待优化的机床部件构建的模型为三维模型时，第二维、第三维和第四维的取值分别为二维模型中在高长宽维度上的设计变量的数量，维度乘积与设计变量总数一致。

19、所述的步骤2)中，融合概率分布卷积层的神经网络的包括信息散度值的损失函数loss具体如下：

20、loss＝loss1+ω·loss2

21、

22、

23、其中，loss1和loss2分别为均方根误差损失和信息散度损失；ω为融合概率分布卷积层的神经网络的预设第一权重参数，由两个损失函数的数量级差距决定；n为输入融合概率分布卷积层的神经网络中的初始样本组的组数；fk(ρ)为第k组初始样本组的目标函数网络预测值，fk(ρ)为输入优化目标函数中获得的的第k组初始样本组的目标函数值；kl为信息散度值；qθ为近似分布，w为融合概率分布卷积层的神经网络的预设第二权重参数，d为分布参数，p为先验分布，||为条件概率分布的符号。

24、损失函数的第一部分loss1是神经网络预测值与训练样本点的有限元计算结果值的均方误差；损失函数的第二部分loss2是加入概率分布卷积层网络输出的信息散度值kl，这里用到了bayes by backprop这种变分推理方法，利用一个近似分布，通过信息散度值来使得网络参数越来越接近于真实的后验分布。

25、所述的步骤5)中，利用高斯过程模型和预期期望采集函数对机床结构优化神经网络进行寻优，具体如下：

26、5.1)获取在步骤4)中机床结构优化神经网络输出的各个有限元节点处的密度值集合ρ的目标函数均值f(ρ)_a和目标函数标准差f(ρ)_δ，从而构建高斯过程模型。

27、5.2)使用预期期望ei(expected improvement)采集函数对高斯过程模型进行全局最小值搜索寻优后获得当前的最优候选组。

28、5.3)判断当前的寻优后的机床结构优化神经网络是否收敛或者达到预设迭代次数阈值，若是则输出当前的最优候选组作为最终的设计变量的最优候选组，即最终的各个有限元节点的最优密度值，若否则将当前的最优候选组加入各组初始样本组中后作为当前的寻优后的机床结构优化神经网络的输入，并重复步骤5.1)-5.3)中机床结构优化神经网络的相同的操作，直至获得最终的设计变量的最优候选组。

29、当寻优后的机床结构优化神经网络预测的最优候选组的目标函数网络预测值和根据优化目标函数获得的最优候选组的目标函数值之间的差值小于预设差值阈值，则判断寻优后的机床结构优化神经网络收敛。

30、所述的步骤5)中，在最优候选组附近添加扰动，即根据遗传算法，对最优候选组添加突变、交叉和卷积的扰动，从而获得若干组新样本组。

31、在最优候选组附近添加扰动，使得算法在前面训练样本点的基础上增加样本点数量，参照遗传算法的思路，添加的扰动可以分类为突变、交叉和卷积；突变意味着对这组最优解用随机数替换一个或多个设计变量，即改变其中一个或者几个有限元节点的密度值，交叉意味着交换这组设计变量中的几个元素，即交换其中几个有限元节点的密度值，卷积意味着对这组设计变量应用给定卷积核，即对其中一块区域中的各个有限元节点的密度值进行卷积运算。

32、本发明的一种电子设备，包括：相互耦接的存储器和处理器，其中，所述存储器存储有程序数据，所述处理器调用所述程序数据以执行如上述所述的方法。

33、本发明的有益效果是：

34、本发明通过对网络输入维度的调整，可以同时适用于二维设计和三维设计，可在保证设计精度的情况下，大幅缩短优化时间，不受设计维度的局限。本发明通过在给定约束下的拓扑优化中，融合概率分布卷积层，将拓扑优化问题中的设计变量转换为图像检测问题中的像素点，利用卷积层卷积核使得设计变量之间的联系变得更为紧密，提升拓扑优化的计算精度和计算效率；通过高斯过程模型与预期期望采集函数代替传统梯度优化方法，可以克服网络寻优陷入局部最小值，从而使得方法适用于大规模复杂问题。本发明通过融合自导向在线学习，使得新一批样本点精准生成在当前问题感兴趣的区域，可以达到减小模型计算量的效果，使预测最优解收敛于全局最优解，加快收敛速度，最终实现机床结构优化。