一种单关节不同运动想象脑电信号在线识别方法

本发明涉及电信号分类识别研究技术，具体涉及一种单关节不同运动想象脑电信号在线识别方法。

背景技术：

1、目前，虽然出现了许多帮助残疾患者的运动辅具，但由于这些外部辅具需要患者存有一定的运动能力去使用，因此对那些因神经障碍而完全丧失运动能力的患者并不友好。随着脑科学以及人工智能等的重大进展，脑机接口技术为运动能力完全丧失的患者使用这些辅具提供了可能。脑机接口技术(brain computer interface，bci)是一种软件与硬件高度结合的技术，它允许人通过脑电信号(electroencep-halogram，eeg)直接与周围环境进行交互，而不依赖于外周神经和肌肉组织。目前，脑机接口可利用的eeg共有三种，分别为外界刺激诱发eeg、p300eeg以及运动想象eeg，其中由于运动想象eeg具有触发灵活，使用者主动性强等优点，因此得到了广泛的应用。

2、采用运动想象eeg帮助患者实现辅具运动主要可分为信号处理、特征提取和分类识别三个流程，不少学者针对这三个流程提出了大量的处理方法，然而由于运动想象eeg的微弱性、特异性以及非平稳性，导致很多方法在实际应用中未能取得良好的效果。首先，在信号处理方面，为了滤除信号中的噪声，提取任务相关成分，不少非线性信号分解方法被引进，例如小波分解以及经验模态分解等，然而由于方法的自身局限性，经常会导致分解信号出现失真现象。其次，在特征提取方面，广泛使用的共空间模式在脑电信号二分类问题中表现了显著的优越性，然而对于多分类问题却并不适用。最后，在分类识别方面，现有的分类模型复杂度较高，因此实际在线识别中，模型必然存在时延问题。

3、因此，提供一种特征提取能力强、分类性能高的多类运动想象脑电信号识别方法已成为本领域研究人员亟待解决的技术问题。

技术实现思路

1、本发明的主要目的在于提供一种单关节不同运动想象脑电信号在线识别方法，实现对多类运动想象脑电信号的分类识别。

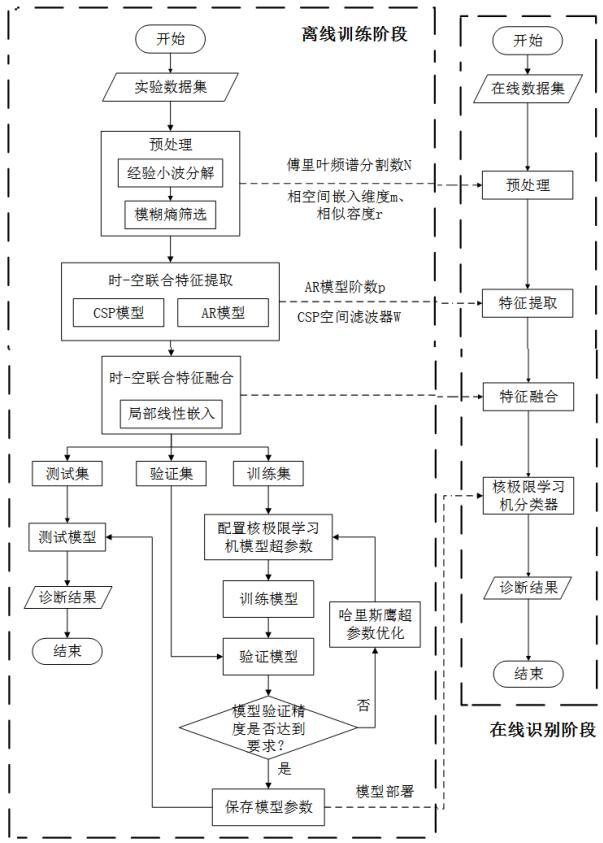
2、本发明采用的技术方案是：一种单关节不同运动想象脑电信号在线识别方法，包括：

3、s1，使用脑电采集设备采集不同试者不同动作的多导联运动想象脑电信号；

4、s2，利用巴特沃斯滤波器和共平均参考对采集的脑电信号进行预处理，并采用无参自适应经验小波变换将预处理后的各导联脑电信号分解为一系列模态分量，通过计算各模态的模糊熵值并选取各导联中熵值最大的模态分量重构脑电信号矩阵；

5、s3，采用ar模型算法，提取重构脑电信号矩阵的时域特征，采用共空间模式算法提取重构脑电信号矩阵的空域特征；

6、s4，将时域特征与频域特征进行拼接，并采用局部线性嵌入算法对其进行融合，得到最终的特征；

7、s5，构建混合核极限学习机模型，将步骤s4中提取的特征向量按照6:2:2的比例划分为训练集、验证集和测试集，通过训练集对核极限学习机的参数进行训练，通过验证集结合哈里斯鹰优化算法对核极限学习机的参数进行优化，得到最优的核极限学习机分类模型，通过测试集对最优的核极限学习机进行实际使用验证；

8、s6，使用测试集验证的性能良好的核极限学习机对实时采集的脑电数据进行分类识别。

9、进一步地，所述步骤s2包括：

10、s21，选取运动想象有关的多导联脑电信号xi(t)∈rl×m，其中t为采样点数，i为导联数，其中t＝1,2,···,l，i＝1,2,···,m；

11、s22，采用4阶巴特沃斯滤波器将脑电信号xi(t)的频带滤波至8-30hz，得到滤波后的脑电信号为si(t)；

12、s23，利用共平均参考对滤波后的脑电信号si(t)进行降噪，得到降噪后的信号yi(t)；

13、

14、s24，对脑电信号yi(t)进行傅里叶变换并标准化到[0,π]区间，得到频域信号yi(ω)；

15、s25，采用尺度空间法将yi(ω)(ω∈[0,π])自适应划分为n个子频带；

16、s26，根据meyer小波理论在每个子频带上构造小波滤波器：

17、

18、

19、式中，φn(ω)和ψn(ω)分别为经验小波的尺度函数和小波函数，β(y)为定义在[0,1]之间的函数，这里取β(y)＝y4(35-84y+70y2-20y3)，

20、

21、对于所述的脑电信号yi(t)，其小波函数的细节参数和尺度函数的细节参数分别定义为：

22、

23、

24、式中，yi(ω)、和分别为离散化的脑电信号、小波函数值和尺度函数值；

25、最终，所述的yi(t)经过经验小波分解得到如下经验模态：

26、

27、s27，对于各导联脑电信号的模态分量定义其相空间嵌入维度w(w＜l-1)和相似容度r，重构相空间：

28、

29、

30、首先，计算窗口向量和的最大距离：

31、

32、然后，计算的模糊隶属度并求取所有的均值

33、

34、

35、接着，计算所有窗口向量的的均值：

36、

37、最后，重复s41-s44，计算并在此基础上求得的模糊熵为：

38、

39、s28，选择具有最大模糊熵值的并采用经验小波逆变换重构各导联脑电信号yi(t)：

40、

41、其中，和ψmax(t)分别为具有最大模糊熵值对应的小波函数值和小波函数细节参数值。

42、更进一步地，所述步骤s25包括：

43、s251，将脑电信号的频域函数yi(ω)离散化，得到离散信号

44、s252，定义的尺度空间函数：

45、

46、其中，为高斯核函数，σ为尺度参数，λ为离散函数的移动步长，m为离散函数移动的最大步长；

47、为了离散化尺度空间函数，离散化尺度参数σ：

48、

49、其中，s＝1,2,···,smax，smax＝2ωmax；

50、s253，找出的全部极小值点并计算尺度空间函数在所有极小值点处的尺度叠加值li，采用otus法确定li的阈值，保留大于阈值的li所对应的极小值点ωli，并以此为分界点对进行分割。

51、更进一步地，所述步骤s3包括：

52、s31，采用p阶ar模型拟合单通道运动想象脑电信号yi(t)：

53、

54、其中，yi(n)表示信号的第n个采样值，p是ar模型的阶数，ak是ar模型的系数(k＝1,2,…,p)，s(n)为均值为0，方差为σ2的白噪声残差；

55、s32，采用burg算法对s41所述的ar模型的ak进行求解；

56、s33，将m个通道的p阶ar系数连接成行向量，得到重构信号的时域特征向量如下：

57、fs＝[a11,a12,...,a1p,...,am1,am2...,amp]

58、s34，对于两类运动想象任务的信号矩阵u1和u2，将u1和u2归一化后分别计算它们的协方差r1和r2以及它们的混合协方差r：

59、

60、

61、

62、其中，和分别表示第一类和第二类运动想象任务的所有样本的协方差均值；

63、首先，对混合些方差矩阵进行特征值分解，并计算白化矩阵：

64、r＝qλqt

65、

66、其中，q为r的特征向量矩阵，λ为r的特征值组成的对角阵，p为白化矩阵；

67、然后，分别对r1和r2进行白化和主分量分解，得到共同的特征向量矩阵b:

68、s1＝pr1pt,s2＝pr2pt

69、

70、其中，s1和s2分别为r1和r2白化处理后的矩阵，b1和b2分别为s1和s2的特征向量矩阵，λ1和λ2分别为s1和s2的特征值，其中λ1+λ2＝i,则：

71、b＝b1＝b2

72、接着，取b的前b行和后b行，构造空间滤波器：

73、w＝btp

74、最后，采用“ovo”策略，对于g类运动想象任务共构造g(g-1)/2个空间滤波器，将这些滤波器进行拼接，构造总的滤波器为：

75、w＝[w1；w1；···；wg]

76、s35，对第g类运动想象的单次样本ug进行空间滤波并提取行方差特征：

77、zg＝wug

78、

79、其中，zg和fg分别为ug的滤波矩阵和特征向量。

80、更进一步地，所述步骤s32包括：

81、s321，定义k阶前向预测误差序列为fk(n)，k阶后向误差预测序列bk(n)，初始化k＝0,f0(n)＝b0(n)＝yi(n)，初始化ak＝1，ar＝0(r＝1,2,…,p)；

82、s322，计算第k+1阶反射系数uk+1：

83、

84、s323，采用下式估计k+1阶ar模型系数：令ar′＝ar+uk+1ak+1-r(r＝1,2,…,k+1)，再令ar＝ar′；

85、s324，判断k+1＝p是否成立，若否，则进入步骤s425，若是，则停止计算，得到p阶ar模型系数ak；

86、s325，采用下式估算k+1阶前向预测误差序列以及k+1阶后向预测误差序列：

87、fk+1(n)＝fk(n)+uk+1bk(n-k-1)

88、bk+1(n)＝bk(n)+uk+1fk(n+k+1)

89、令k＝k+1，返回步骤s322。

90、更进一步地，所述步骤s4包括：

91、s41，将时域特征向量fs和空域特征向量fg进行特征拼接，得到联合特征向量f＝[fs；fg]；

92、s42，定义f＝[f1,f2,...,f2]为降维的数据矩阵，其中fi为第i个样本的联合特征向量，以欧式距离为准则，计算每个样本点fi的最近k个临近的点集合qi，其中qi＝[fi1,fi2,...,fik]，对fi进行线性表示为：

93、fi＝si1fi1+si2fi2+...+sikfik

94、其中，si＝[si1,si2,...,sik]为相应的权重；

95、s43，将线性权重等价为一个回归问题，定义损失函数：

96、

97、

98、以及协方差矩阵：

99、z＝(fi-qi)(fi-qi)t,i∈[1,k]

100、其中，1k为全1的列向量，z是k×k的矩阵，j是k的索引，运用拉格朗日法，可以转化为：

101、

102、s44，对lf(si)进行求导，得到权值系数矩阵：

103、

104、

105、s45，将s64中得到的权值系数矩阵向低维进行映射，并满足：

106、

107、其中，yi表示fi在低维空间上的投影，对于不在样本点邻域位置内的si取值为0，然后扩充权重矩阵到整个数据集的维度，矩阵化后上式转化为：

108、

109、其中，ii表示单位矩阵i的第i列，令m＝(i-s)(i-s)t,在一次使用拉格朗日乘数法：

110、ly(y)＝tr(ymyt)+λ(yyt-pi)

111、s46，为得到d维的数据集，将m的特征值从小到大排列，取最小的d个非零特征值所对应的特征向量作为降维后的的输出结果，得到数据矩阵y′∈rd×p。

112、更进一步地，所述步骤s5包括：

113、s51，初始化输入层和隐含层间的连接权值和隐含层神经元的阈值，设置隐含层神经元的个数，单隐层神经网络的输出为：

114、f(y′)＝h(y′)×β

115、式中，y′为输入数据向量，f(y′)为网络输出；h(x)为隐含层节点输出函数；β为连接隐含层和输出层的输出权值向量；

116、将网络训练变为线性系统求解问题，引入正则化系数c和单位矩阵i，则隐含层与输出层的输出权值为：

117、

118、s52，选择径向基核函数和多项式核函数的混合加权作为核极限学习机的核函数，通过对原始高维数据输入乘以隐藏层与输出层之间的权值矩阵实现降维：

119、

120、其中，k(yi,yj)为核极限学习机的混合核函数，η，ξ为混合核函数的参数；

121、此时，混合核函数的输出为：

122、

123、s53，通过验证集识别准确率构造目标函数，目标函数定义如下：

124、

125、其中，acc代表验证集识别准确率，nci为第i类正确分类个数，nei为第i类错误分类个数，l为总类别个数；

126、s54，将哈里斯鹰优化算法用于上述目标函数，通过全局搜索阶段、搜索到开发阶段以及开发阶段获得混合核极限学习机的核参数最优值，其中，全局搜索阶段通过两种策略更新参数向量(哈里斯鹰)的值：

127、

128、其中，h(t)为当前鹰的位置向量，hrabbit(t)为当前拥有最优适应度的个体位置，hrand(t)为当前种群中随机选择鹰的位置，h(t+1)为下一次迭代过程中鹰的位置向量，r1，r2，r3，r4和q均为(0,1)之间的随机数，lb和ub分别为待优化参数的下限和上限，hm(t)为种群平均位置；

129、根据猎物的能量进行全局搜索阶段与开发阶段的转换，当|e|＜1时进入开发阶段，e的表达式为：

130、

131、其中，e表示猎物的逃逸能量，e0表示能量的初始状态，t表示最大迭代次数；

132、s55，开发阶段根据猎物的能量e以及猎物的逃脱概率gl选择四种攻击方式更新参数向量的位置，其中：

133、当|e|≥0.5且gl≥0.5时采用软包围攻击方式；

134、当|e|≤0.5且gl≥0.5时采用硬包围攻击方式；

135、当|e|≥0.5且gl＜0.5时采用渐进式快速俯冲的软包围攻击方式；

136、当|e|≤0.5且gl＜0.5时采用渐进式快速俯冲的硬包围攻击方式。

137、更进一步地，所述步骤s55包括：

138、s551，当采用软包围攻击方式时，参数向量的位置更新表达为：

139、h(t+1)＝δh(t)-e|jhrabbit(t)-h(t)|

140、δh(t)＝hrabbit(t)-h(t)

141、j＝2(1-r5)

142、其中，δh(t)为最优个体与当前个体之间的差值，r5为(0,1)之间的随机数，j为兔子逃跑过程中的跳跃距离：

143、s552，当采用硬包围攻击方式时，参数向量的位置更新表达为：

144、h(t+1)＝hrabbit(t)-e|δh(t)|

145、s553，当采用渐进式俯冲的软包围攻击方式时，参数向量的位置更新表达式为：

146、

147、y＝hrabbit(t)-e|jhrabbit(t)-h(t)|

148、z＝y+s×lf(d)

149、fitness(·)＝1-acc(·)

150、其中，fitness(·)为参数向量的适应度值，d是问题的维数，s是1×d维的向量，lf是莱维飞行函数，其表达式为：

151、

152、

153、其中，μ，υ是(0,1)之间的随机变量，β为设置为1.5的常量；

154、s554，当采用渐进式俯冲的硬包围攻击方式时，参数的位置更新表达式为：

155、

156、y＝hrabbit(t)-e|jhrabbit(t)-hm(t)|

157、z＝y+s×lf(d)。

158、本发明的优点：

159、本发明的一种单关节不同运动想象脑电信号在线识别方法，首先采用经验小波变换将预处理后的脑电信号自适应分解为一系列模态分量，有效避免了信号分解过程中的模态混叠现象，并通过模糊熵算法筛选了最优的模态分量构成新的信号矩阵，消除了不相干频段的影响，精炼了信号的频率特征；接着通过采用ar模型算法提取信号的时域特征，采用共空间模式算法提取信号的空域特征，并通过采用局部线性嵌入算法对其进行融合，增强了特征信息，降低了特征维度；最后，使用核极限学习机提升了特征识别的效率，其中通过哈里斯鹰算法优化核极限学习机的超参数，改善了分类器的分类性能，提高了多类运动想象脑电信号的识别准确率。

160、除了上面所描述的目的、特征和优点之外，本发明还有其它的目的、特征和优点。下面将参照图，对本发明作进一步详细的说明。