一种基于数字仿真与OBB包围盒的活动线缆碰撞检测方法

本发明属于计算机仿真，具体涉及一种活动线缆碰撞检测方法。

背景技术：

1、在机载卫星系统工作的过程中，天线阵面由跟踪伺服转台带动，不停做往返旋转运动，伺服机构上的多根线缆也在跟随运动，这些线缆被称为活动线缆。由于活动线缆会影响伺服机构的理想工作状态，在线缆装配前对活动线缆的运动形态进行研究尤为重要。

2、目前关于活动线缆的力学仿真研究中很少提及线缆间碰撞的情景。然而，假如活动线缆间存在相互碰撞现象，碰撞线缆的位姿和其对伺服机构产生的干扰力矩，都会较按未考虑碰撞时的仿真结果出现较大的变化。因此，在仿真过程中进行碰撞检测非常重要。

3、文献(金望韬,刘检华,刘佳顺,等.光滑平面约束下的活动线缆物理特性建模与运动仿真技术[j].机械工程学报,2016,52(3):118-127.)利用kirchhoff弹性细杆理论对活动线缆进行力学建模，提出一套微分方程组表达线缆微元的力学特性。但是该方法未考虑活动平面转动后线缆的位姿变化，同时忽略了多根线缆发生碰撞的实际工况，在工程应用中存在一定局限性。

4、文献(王发麟,郭宇,廖文和,黄少华.基于距离场和扫掠剪除算法的线缆碰撞检测技术[j].计算机工程与应用,2017,53(10):27-33.)利用包围球层次结构、距离场和扫掠剪除算法的方法进行碰撞检测，提出一种基于三维距离场映射的碰撞检测方法。但是该方法所研究的线缆形状与本发明检测的线缆有所差别，同时该方法未考虑运动过程中的碰撞检测，仅对某一时刻运动线缆的位姿状态进行碰撞检测，所以该方法并不适用于本发明面向的工程应用场景。

5、目前活动线缆碰撞检测的相关方法存在以下局限性：

6、1.对活动线缆进行位姿仿真时没有考虑其运动特性，难以在活动线缆随平面转动的每一时刻给出对应的线缆位姿，从而更难考虑活动线缆在运动过程中是否发生碰撞；

7、2.对不同线缆相互碰撞的检测方法主要为计算多个包围球或aabb包围盒间是否发生相交。这些方法存在时间复杂度高的局限性，同时对于原本不可能碰撞的线缆，以及特殊形态的线缆(如悬链线)存在较多的冗余计算。

技术实现思路

1、为了克服现有技术的不足，本发明提供了一种基于数字仿真与obb包围盒的活动线缆碰撞检测方法，首先建立一根活动线缆力学模型；接下来求解一根活动线缆位姿；然后预检测两根活动线缆是否可能发生碰撞；之后建立两根活动线缆的包围盒模型；最后判断两根活动线缆的包围盒是否发生相交。本发明采用kirchhoff弹性细杆理论建立活动线缆的力学模型，可以较好的体现线缆的弯曲、扭转特性。

2、本发明解决其技术问题所采用的技术方案如下：

3、步骤1：建立一根活动线缆力学模型；

4、活动线缆力学模型建立在kirchhoff弹性细杆理论的基础上；活动线缆力学模型由一组微分方程组成，用于描述在不同载荷和约束条件下，细杆的弹性和塑性响应；

5、该步骤用到的变量定义如下：

6、po：活动线缆固定端端点；

7、pl：活动线缆活动端端点；

8、l：活动线缆长度；

9、p-xyz：以线缆微元段截面中心为原点，微元段副法向、切向和法向为轴向的frenet坐标系；

10、o-ξηζ：以o为原点建立笛卡尔三维惯性坐标系，为全局坐标系；

11、fi：线缆微元段截面受到邻近截面作用内力主矢在i轴方向的分力；

12、s：线缆微元段截面上的弧坐标，即从po开始的弧长距离；

13、t：线缆微元段截面切线方向的单位向量；

14、ωi：线缆微元段截面在i轴方向的弯扭度；

15、ki：线缆微元段截面绕i轴的抗弯刚度/抗扭刚度；

16、e：活动线缆的杨氏模量；

17、g：活动线缆的剪切模量；

18、ji：线缆微元段截面对i轴的惯性矩；

19、dp：线缆微元段截面直径；

20、q1,q2,q3,q4：线缆微元段截面的欧拉四元数；

21、步骤1-1：建立全局坐标系o-ξηζ，输入待建模活动线缆的长度l、固定端端点坐标po、活动端端点坐标pl、杨氏模量e、剪切模量g、截面直径dp；

22、步骤1-2：将活动线缆按长度平均划分为10个微元段；

23、步骤1-3：根据公式代入活动线缆的e、g、dp计算出活动线缆微元段的抗弯刚度/抗扭刚度ki；

24、步骤1-4：用欧拉四元数q1,q2,q3,q4表示弯扭度ωi；弯扭度和欧拉四元数的代数关系为：

25、

26、其中

27、步骤1-5：建立关于线缆微元段的kirchhoff受力平衡方程组：

28、

29、该方程组由frenet坐标系下三个轴向上的力的平衡与力矩平衡构成；平衡方程组和方程构成了本质上为7个未知数fx、fy、fz、q1、q2、q3、q4和7个方程的微分方程组；

30、步骤1-6：按照步骤1-3～步骤1-5的方式建立10个线缆微元段的kirchhoff受力平衡方程组；

31、步骤1-7：增加线缆的几何约束；

32、由于活动线缆的长度和活动点坐标为已知量，需要增加4个几何约束方程，包括：

33、

34、

35、至此，单根活动线缆的70个未知量，74个方程的超定微分方程组建立完毕，该方程组即为活动线缆力学模型；

36、步骤2：求解一根活动线缆位姿；

37、求解活动线缆位姿即求解步骤1建立的超定方程组，再通过解得的已知量计算活动线缆每个离散点的全局坐标；

38、该步骤用到的变量定义如下：

39、cn：第n阶导的权系数矩阵；

40、n：离散点的数量；

41、si：活动线缆上第i个的点的弧坐标；

42、步骤2-1：将方程组的微分项离散为权系数矩阵第n阶导的元素与函数值的乘积的和；

43、n阶导数表示为其中

44、权系数矩阵的计算由离散点的选择方式决定，使用chebyshev方法选取离散点，即在离散化处理后，方程组中的微分项都被替换成了由离散点构成的一阶多项式的形式；

45、步骤2-2：将求解超定代数方程组的问题转化为优化问题；

46、设超定代数方程组中第j个方程的表达式为fj(x)＝0，则代数方程组为f(x)＝(f1(x),f2(x),…,ft(x))t＝0，f(x)是方程组的残差形式；

47、优化问题的目标函数定义为：

48、

49、步骤2-3：运用levenberg-marquard法求解非线性优化问题；

50、输入包括向量函数f(x)＝(f1(x),f2(x),…,ft(x))t，解向量的初值x0，以及收敛条件εx,εg，输出包括超定代数方程组的解向量；

51、步骤2-4：利用方程组的解计算活动线缆离散点的全局坐标；

52、活动线缆离散点坐标与欧拉四元数有关，计算公式为：

53、

54、活动线缆上每个离散点的全局坐标已经解出，在活动平面的一个转动角度下，不考虑碰撞情景的单根线缆位姿仿真已完成；

55、步骤3：预检测两根活动线缆是否可能发生碰撞；

56、判断n根活动线缆是否发生碰撞，等价于判断n根活动线缆中所有的线缆对中，是否存在发生碰撞的线缆对，两根线缆组成一个线缆对，既n根线缆中存在个不同的线缆对；若不存在发生碰撞的线缆对，则判定n根活动线缆未发生碰撞；若存在任意发生碰撞的线缆对，则判定n根活动线缆发生碰撞；

57、该步骤用到的变量定义如下：

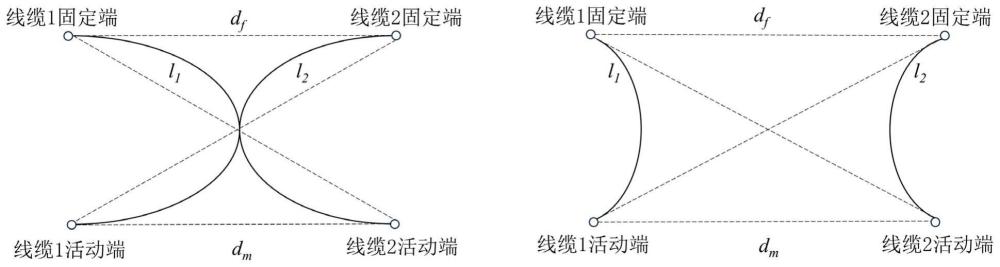
58、l1：活动线缆1的长度；

59、l2：活动线缆2的长度；

60、dm：活动线缆1活动端坐标与活动线缆2活动端坐标的距离；

61、df：活动线缆1固定端坐标与活动线缆2固定端坐标的距离；

62、步骤3-1：已知活动线缆1和活动线缆2的活动端和固定端坐标，利用两点间距离公式求出dm和df；

63、步骤3-2：若满足l1+l2<dm+df时，判断活动线缆1和活动线缆2之间不会发生碰撞，不需要进行步骤4和步骤5；若不满足上式，则活动线缆1和活动线缆2之间可能发生碰撞，需要进行步骤4和步骤5进一步进行检测；

64、步骤4：建立两根活动线缆的包围盒模型；

65、该步骤用到的变量定义如下：

66、ξi：活动线缆第i个离散点在全局坐标系o-ξηζ下的ξ轴坐标值

67、ηi：活动线缆第i个离散点在全局坐标系o-ξηζ下的η轴坐标值

68、ζi：活动线缆第i个离散点在全局坐标系o-ξηζ下的ζ轴坐标值

69、ω1：一根活动线缆的离散点集合被分割平面划分后部分点形成的点集

70、ω2：一根活动线缆的离散点集合被分割平面划分后另一部分点形成的点集

71、μξ：一个点集中所有点ξ轴坐标的平均值

72、μη：一个点集中所有点η轴坐标的平均值

73、μζ：一个点集中所有点ζ轴坐标的平均值

74、a：根据一个点集中的坐标值和平均值得到的3行3列协方差矩阵

75、box：记录obb包围盒所有信息的数组(包括9个元素)

76、b：包围盒中心点

77、ξbox：obb包围盒中心点的ξ轴坐标

78、ηbox：obb包围盒中心点的η轴坐标

79、ζbox：obb包围盒中心点的ζ轴坐标

80、r：从全局坐标系o-ξηζ到obb包围盒坐标系b-123的基变换矩阵

81、r1：从全局坐标系o-ξηζ到obb包围盒坐标系b-123的基变换矩阵第一行(3维行向量)

82、r2：从全局坐标系o-ξηζ到obb包围盒坐标系b-123的基变换矩阵第二行(3维行向量)

83、r3：从全局坐标系o-ξηζ到obb包围盒坐标系b-123的基变换矩阵第三行(3维行向量)

84、he1：obb包围盒在协方差矩阵特征向量1方向的半长轴

85、he2：obb包围盒在协方差矩阵特征向量2方向的半长轴

86、he3：obb包围盒在协方差矩阵特征向量3方向的半长轴

87、步骤4-1：活动平面在-30°～30°范围内转动时，对活动线缆1在此过程中由步骤2得到的所有离散点坐标的η轴坐标进行排序，找到包含最小η轴坐标的离散点；

88、步骤4-2：过该点做平行于ξoζ平面的分割平面，将线缆运动过程中所有离散点分为ω1和ω2两个点集；

89、步骤4-3：求出ω1中所有点在ξ轴、η轴、ζ轴的平均值μξ、μη、μζ、，其中n为ω1中点的个数，μη、μζ的求法同μξ，包围盒的中心点坐标即为μξ、μη、μζ；

90、步骤4-4：计算ω1中所有点的坐标形成的协方差矩阵a，其中cov(ξ,η)＝e[(ξi-μξ)(ηi-μη)],i∈ω1，e表示取平均值；

91、步骤4-5：计算a的3个特征向量并单位正交化，得到以点b(μξ,μη,μζ)为原点，a的3个特征向量为方向的obb包围盒坐标系b-123；

92、步骤4-6：计算从全局坐标系o-ξηζ到obb包围盒坐标系b-123的基变换矩阵r，取第一行为r1，第二行为r2，第三行为r3；

93、步骤4-7：利用r求出ω1中所有点在obb包围盒坐标系b-123中的坐标值，并利用排序找到三个轴向上各自绝对值最大的的三个正数，将其定义为包围盒的半长轴he1、he2和he3；

94、步骤4-8：建立box数组，box＝{μξ,μη,μζ,r1,r2,r3,he1,he2,he3}，box可以表示ω1生成的包围盒中的所有特征；

95、步骤4-9：对ω2点集重复步骤4-3～步骤4-8；

96、步骤4-9：对活动线缆2重复步骤4-1～步骤4-9。

97、步骤5：判断两根活动线缆的包围盒是否发生相交；

98、使用分离轴定理sat确定活动线缆1和活动线缆2的包围盒是否相交；

99、该步骤用到的变量定义如下：

100、s：包围盒1和包围盒2可能存在某一条的分离轴：分离轴共有15种可能性，分别为平行于包围盒1和包围盒2某一面法向量的3×2共6根轴，以及平行于包围盒1某一边和包围盒2某一边公垂线的3×3共9根轴；

101、b1：包围盒1中心点即包围盒1坐标系原点；

102、b2：包围盒2中心点即包围盒2坐标系原点；

103、bs1：包围盒1中心点在s上的投影点；

104、bs1：包围盒1中心点在s上的投影点；

105、ds12：b1、b2连线在s上的投影线段的长度；

106、rs1：包围盒1在s上的投影半径的长度；

107、rs2：包围盒2在s上的投影半径的长度；

108、ωs1：计算rs1需要的点集；

109、ωs2：计算rs2需要的点集；

110、步骤5-1：根据b1、b2坐标值计算直线b1b2的方程；

111、步骤5-2：根据包围盒坐标系的主轴方向向量与半长轴长度，计算包围盒1、包围盒2每个面的平面方程；

112、步骤5-3：根据步骤5-2得到的12个平面方程和b1b2的直线方程，计算b1b2与包围盒1、包围盒2各自的一个交面，包围盒1上交面的4个顶点形成点集ωs1，包围盒2上交面的4个顶点形成点集ωs2；

113、步骤5-4：从15条分离轴中选出一条未计算的分离轴s。根据两个包围盒坐标系某一主轴的方向向量，或两个包围盒坐标系各自某一主轴方向向量叉乘后的方向向量，确定s的方向向量；

114、步骤5-5：过b1、b2做两个垂直于s的平面，这两个平面与s的交点为b1、b2在s上的投影bs1、bs2，利用两点间距离公式计算bs1、bs2的距离ds12；

115、步骤5-6：将ωs1中的4个点以步骤5-5的方式投影至s上，其中满足bs1到投影点的方向为bs1bs2且距离bs1最远的一点为包围盒1在s上的投影点，该投影点到bs1的距离为rs1；

116、步骤5-7：将ωs2中的4个点以步骤5-5的方式投影至s上，其中满足bs2到投影点的方向为bs2bs1且距离bs2最远的一点为包围盒2在s上的投影点，该投影点到bs2的距离为rs2；

117、步骤5-8：若满足ds12>rs1+rs2，判断包围盒1与包围盒2不相交；否则返回步骤5-4根据下一根可能的分离轴计算两包围盒是否相交；如果对于15条可能存在的分离轴，ds12>rs1+rs2都不成立，则判断包围盒1与包围盒2相交；此时计算线段b1b2的中点坐标，记该点位置为碰撞发生位置；

118、步骤5-9：若活动线缆1的两个包围盒与活动线缆2的两个包围盒都不相交，则判断活动线缆1和活动线缆2未发生碰撞，输出线缆未发生碰撞；若四次包围盒相交检测中有一次包围盒相交出现，则判断活动线缆1和活动线缆2发生碰撞，输出发生碰撞的线缆以及所有碰撞位置。

119、优选地，所述两个包围盒坐标系某一主轴的方向向量等价于面的法向量，共6种；所述两个包围盒坐标系各自某一主轴方向向量叉乘后的方向向量等价于两条边的公垂线，共9种。

120、本发明的有益效果如下：

121、1、本发明采用kirchhoff弹性细杆理论建立活动线缆的力学模型，可以较好的体现线缆的弯曲、扭转特性；

122、2、本发明选用非线性最小二乘法levenberg-marquardt算法进行线缆模型的求解，该方案具有较高的建模精度和较快求解速度的优点，解决了弹性细杆模型难以求解的问题；

123、3、本发明在使用包围盒进行精确碰撞器检测前先进行预检测，排除对不相交线缆间的冗余计算，加快计算执行效率；

124、4、本发明采用了两包围盒(支持扩展为多包围盒)包含一根活动线缆的包围盒生成方式，综合了计算速度和计算精度的双重要求。