一种电机偏心不平衡磁拉力模型构建方法及补偿控制系统

本发明涉及无轴承电机控制，主要涉及一种基于开槽调制效应的电机偏心不平衡磁拉力模型构建方法及补偿控制系统。

背景技术：

1、薄片电机由于其没有机械轴承的特殊结构，故而对转子能否平稳且不偏心的悬浮在中心位置具有很高的要求，而电机的不平衡磁拉力对电机径向悬浮的性能有很大的影响，所以精确解析薄片永磁同步电机的偏心不平衡磁拉力并对其进行补偿，便成了薄片电机能否高质量悬浮的一大重要影响因素。

2、文献“dorrell d g,smith a c.calculation and measurement of unbalancedmagnetic pull in cage induction motors with eccentric rotors.iee proceedingselectric powerapplications,1996,143(3):193-210.”以一维解析法为基础，通过建立转子的磁动势模型，并与气隙磁导率模型相结合，简单直观的得到了偏心时永磁电机的磁场分布情况，但是，对于如静态偏心和动态偏心等不同转子偏心类型没有进行区分，只可做不平衡磁拉力的定性分析。文献“[12]dorrell d g,hsieh m f,guo y g.unbalanced magnetpull in large brushless rare-earth permanent magnet motors with rotoreccentricity.ieee transactions on magnetics,2009,45(10):4586-4589.”推导了区分永磁电机的动、静偏心情况下的不平衡磁拉力模型，提升了模型精度，但其重点分析了不平衡磁拉力的谐波特性，而忽略了不平衡磁拉力的高精度定量分析。上述文章的分析都建立在了一维解析的基础之上，模型精度不够高，只适用于对不平衡磁拉力进行定性分析，用于分析不平衡磁拉力的大小时，误差较大。

3、此外，文献“[15]zhu z q,howe d,bolte e,ackermann b.instantaneousmagnetic field distribution in brushless permanent magnet dc motors.ieeetransactions on magnetics,1993,29(1):124-158.”以子域法为基础，建立了永磁电机的二维磁场分布解析模型，实现了电机解析从一维到二维的转变。在文献“li y,lu q,zhu zq.unbalanced magnetic force prediction in permanent magnet machines withrotor eccentricity by improved superposition method.iet electric powerapplications,2017,11(6):1095-1104.”中，利用子域叠加法，将偏心磁场等效成多个同心磁场的叠加，但没有给出具体的解析式。随后，国内外学者将一阶摄动法与子域法结合，建立了表贴式永磁电机、插入式永磁电机的偏心磁场解析模型，提升了解析精度。为了便于分析，上述模型都没有考虑定子开槽的影响，对传统有轴承这类偏心情况较简单的电机进行定量分析时，精度尚可，但用于偏心情况复杂多变的无轴承薄片电机时，开槽影响所带来的误差难以忽略。

4、文献“于吉坤，李立毅，张江鹏，曹继伟.定子开槽永磁同步电机气隙比磁导解析计算.电工技术学报,2016,31(s1):45-52.”中，开槽调制效应的分析与研究只集中在开槽对定位力矩的影响、开槽对调制转矩的影响以及开槽对气息磁导比的影响，没有涉及开槽对不平衡磁场力的影响和准确建模。

技术实现思路

1、发明目的：针对上述背景技术中存在的问题，本发明提供了一种考虑了定子开槽影响的不平衡磁拉力精确数学模型，从磁场调制的角度分析了偏心时不平衡磁拉力的产生机理，重构了考虑开槽影响的电机偏心不平衡磁拉力，相比于传统的不平衡磁拉力数学模型，本模型的精度更高，更加适用于对薄片电机进行不平衡磁拉力补偿。

2、技术方案：为实现上述目的，本发明采用的技术方案为：

3、一种基于开槽调制效应的电机偏心不平衡磁拉力模型，采用了六齿一对极的电机结构；包括6个l型定子；每个l型定子包括轴向的定子轭和径向定子齿，环绕在薄片状转子周围，径向定子齿与转子平齐，每个轴向定子轭分别绕有悬浮绕组和转矩绕组，所述转矩绕组为一对极，悬浮绕组为两对极，同时实现悬浮控制和旋转控制；所述l型定子底部通过铁心导磁环相连；所述薄片状转子外侧贴有一对极永磁体；基于此电机结构，构建考虑了开槽影响的不平衡磁拉力的数学模型；

4、具体地，首先以定子中心为坐标原点建立θ-os-r定子坐标系，以转子中心为坐标原点建立α-or-β转子坐标系，如图1所示，其中e为悬浮转子偏心距，为电机转子偏心角度，转子按转速ω逆时针旋转，p为转子上任一点，θ为p与定子坐标系横坐标的夹角，ψ为p与转子坐标系横坐标的夹角。由几何关系可知，两坐标系的转换关系如公式(1)所示：

5、

6、根据子域法，永磁体和气隙的子域方程可表示为公式(2)的形式：

7、

8、式中，az1与az2分别是永磁体和气隙子域的矢量磁位，μ0为真空磁导率，其值取4π*10-7h/m，m表示永磁体的磁化强度，在转子坐标系下

9、

10、根据坐标转换公式(1)可知，在定子坐标下

11、

12、在转子坐标系下，α和β分别表示径向和切向的单位向量，mα和mβ分别表示永磁体磁化强度的径向和切向分量，在定子坐标系下，r和θ分别表示径向和切向的单位向量，mr和mθ分别表示永磁体磁化强度的径向和切向分量，br为永磁体剩磁。

13、在矢量磁位下，磁密b、磁场强度h的径向与切向分量可分别表示为

14、

15、其中，μr表示相对磁导率，hr和hθ分别为磁场强度h的径向与分量。

16、根据摄动法，将转子偏心视作摄动，利用式(1)，得到永磁体和转子子域的分界面的边界方程：

17、

18、在定子坐标系下，边界的法向量方程可表示为：

19、

20、其中，er和eθ分别为偏心e的径向与切向单位分量。

21、一对极圆环形永磁体作为电机转子，其偏心状态下的分界面满足以下方程：

22、

23、对方程(8)进行矢量运算可得以下方程：

24、

25、根据摄动法，将式(2)带入式(9)，并在r＝rm处展开，可以得到零阶方程(10)与边界条件式(11)

26、

27、

28、根据边界条件、分离变量法与模型对称性，气隙子域的零阶、一阶解分别为

29、

30、根据摄动理论，可以得到转子偏心时的径向与切向磁密分别为

31、

32、综上，结合方程(12)、(13)，可以得到一对极圆环形永磁转子偏心后的气隙磁密分别为

33、

34、设电机开槽前后的气隙磁密分别为bslotloss和bslot，均为复数形式，其表达式分别为

35、

36、其中，brslotloss和bθslotloss分别是开槽前的径向与切向磁密，brslot和bθslot分别是开槽后的径向与切向磁密，定义开槽调制比ξ(r,θ)来描述任意位置处定子开槽对气隙磁密的影响，记为ξ，其表达式为

37、

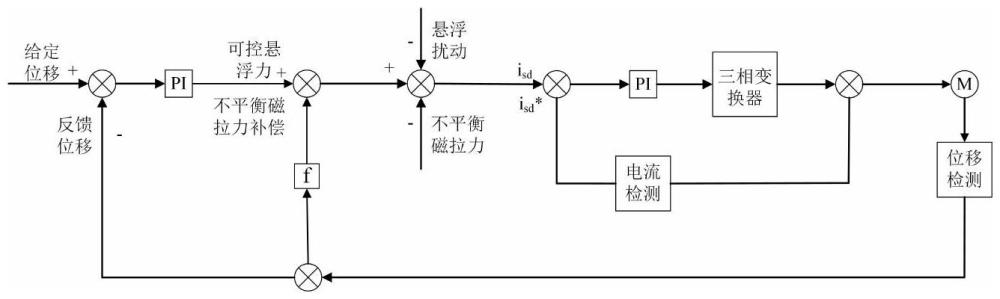
38、开槽调制比的具体表达式，如式(38)所示：

39、

40、式中，r1为定子内径，r2为转子外径，α1为定子槽宽，α2为定子槽口宽，cn(z|k2)、dn(z|k2)、sn(z|k2)、k(k12)分别为三种雅可比椭圆函数和第一类完全椭圆积分。z、k和w的值可通过式(18)和式(19)来确认

41、

42、式中，z(z|k2)为雅可比zeta函数。

43、根据开槽调制比的定义，考虑了开槽影响的偏心气隙磁密分别为

44、

45、进一步的，根据式(20)可以得到考虑了开槽影响的偏心不平衡磁拉力为

46、

47、本发明还提供一种电机位移补偿控制系统，该系统将权利要求1中的不平衡磁拉力模型公式(6)加入到位移补偿控制系统中，具体过程如下：利用位移检测装置检测到反馈位移，将给定位移与反馈位移做差，将位移差值输入pi调节器，得到可控悬浮力；将检测到的位移带入式(6)，得到不平衡磁拉力；可控悬浮力与不平衡磁拉力相加，除以悬浮力系数，得到悬浮电流，利用三相逆变器实现该悬浮电流的闭环。

48、本发明提供的考虑了定子开槽影响的不平衡磁拉力精确数学模型，与现有模型相比，具有以下有益效果：

49、(1)由于考虑了定子开槽所带来的影响，提高了不平衡磁拉力数学模型的精确度。

50、(2)对薄片电机进行不平衡磁拉力补偿时，相比于传统忽略开槽影响的不平衡磁拉力数学模型，补偿效果更好。

51、(3)由于精确补偿了薄片电机的不平衡磁拉力，降低了薄片电机的控制难度，降低了控制成本。

52、(4)精确补偿薄片电机的不平衡磁拉力后，大幅提升了电机的悬浮性能。