基于奥斯特瓦尔德全色域混色模型的色彩调配方法及系统与流程

本发明涉及基于奥斯特瓦尔德全色域混色模型的色彩调配方法及系统，属于色彩配色理论与颜色模型构建及纺织领域的色彩设计方法与应用开发。

背景技术：

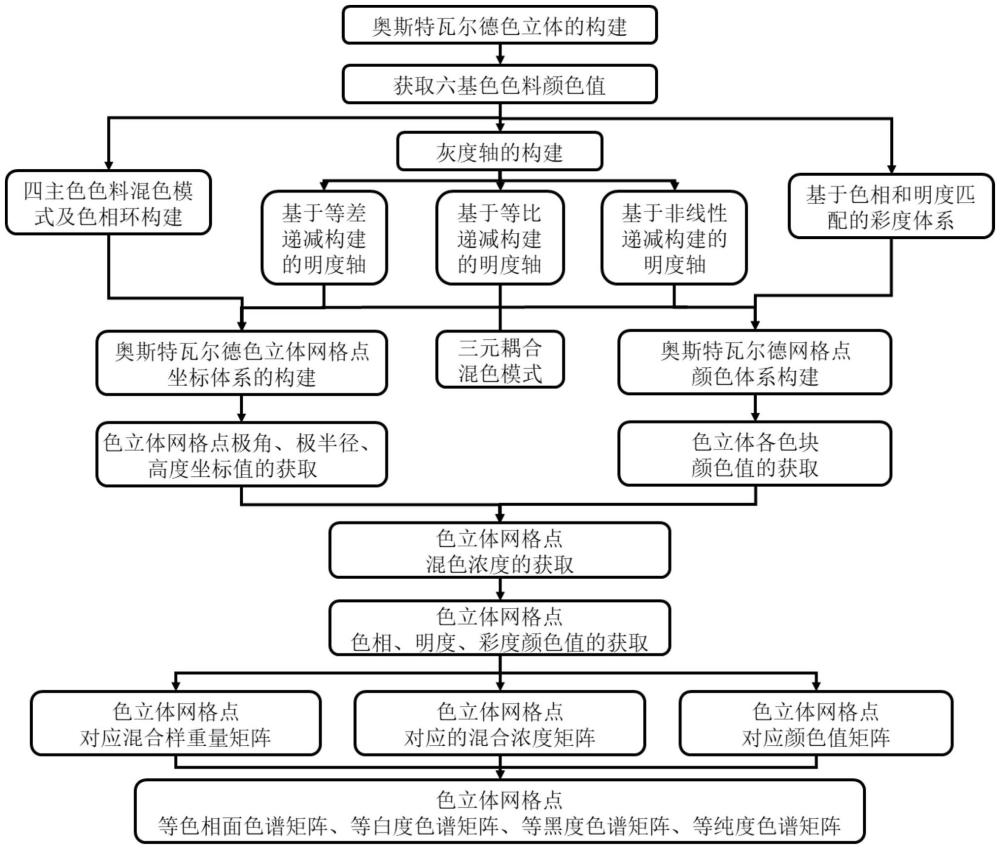
1、奥斯特瓦尔德色立体(ostwald color system)，又称奥氏色立体(ostwald′scolor solid)，它是由24个等色相面、8个等白度面、8个等黑度面组成的三维双圆锥色立体，并通过色相、白度、黑度等三维指标进行表征。

2、奥氏色立体以标准四主色为基础构建了包含24色相的色相环，以标准的白色和黑色为基础构建了从标准白到标准黑的八等级灰度轴，以同等的步度处理各种色相的纯浊变化和明暗变化从而构建了24个等色相面，因此奥氏色立体以一种色彩分布规律解释了色彩与混合比例之间数量关系，然而，奥氏色立体用于工业设计时却存在以下问题：

3、第一，工业生产出来的红、黄、绿、蓝、黑、白主色色料的颜色值并非颜色光学所定义的标准色，四个主色色料的颜色值实际上并不是均匀分布在色相环上的，黑白色实际上也只是接近白色的高明度灰色和最接近黑色的低明度灰色，因此设计师进行调色时，如果以实际六主色色料为基础，而根据标准奥氏色立体的色彩分布规律计算各色料调和浓度的话，就无法获得理想的调色效果，导致较大的调色误差；

4、第二，现有的奥氏色立体仅给出了色卡，即便公开了色彩分布的规律，但是设计师在调色时并无法直接获取各色料的混合比例，再结合上述六主色实际颜色值带来的误差，只能人工对照色卡不断调整各色料的用量，调色效率很低，因此现有的奥氏色立体无法应用于高效精准的工业色彩设计。

技术实现思路

1、为了提供一种可以应用于实际工业色彩设计的奥氏色立体，降低色差，提高调色效率，本发明提供了基于奥斯特瓦尔德全色域混色模型的色彩调配方法及系统，所述技术方案包括：

2、本发明的第一个目的在于提供一种色彩调配方法，包括：

3、步骤一：基于实际测色获取奥斯特瓦尔德色立体的六基色色料的颜色值，构建奥斯特瓦尔德全色域网格化混色模型；

4、步骤二：从所述奥斯特瓦尔德全色域网格化混色模型中获取目标色彩，根据所述目标色彩在模型中的网格点坐标获取调配该色彩所需要的六基色的混合浓度值；

5、步骤三：基于步骤二获取的混合浓度将六基色色料混合，得到目标色料；

6、所述奥斯特瓦尔德全色域网格化混色模型的构建过程包括：

7、步骤1：以红、黄、绿、蓝色料的颜色值为基准，构建奥斯特瓦尔德色立体的色相环，包括：

8、构建四个混色区间，以所述混色区间两个端点的颜色值为基准进行二元耦合混色，得到奥氏色立体色相环上各色相的颜色值c(ξ)，表示为：

9、

10、调配奥氏色立体色相环上各色相的混色浓度为：

11、

12、其中，ξ表示所述奥斯特瓦尔德色立体色相环上各色相的网格点序号，εm≥2；δ＝1，2，3，4分别表示四个混色区间的序号；[rα(δ),gα(δ),bα(δ)]、[rβ(δ),gβ(ξ),bβ(δ)]分别表示第δ个混色区间两个端点的颜色值；和分别表示第ξ个网格点对应颜色的混色区间端点颜色cα(δ)和cβ(δ)的混合浓度，所述混合浓度的递增梯度为1/εm；

13、所述奥斯特瓦尔德色立体色相环上各色相的网格点坐标值为：

14、

15、其中，θξ、ρξ和zξ分别表示网格点的极角、极半径和高度；

16、步骤2：以白、黑色料的颜色值作为最高明度节点和最低明度节点的颜色值，构建奥斯特瓦尔德色立体的灰度轴，所述灰度轴上8个节点的极坐标为：

17、

18、所述灰度轴上8个节点对应的颜色值与混合浓度通过等比递增或等差递增或非线性递增的方式获取；

19、所述灰度轴8个节点的浓度值矩阵为：

20、

21、所述灰度轴8个节点的颜色值矩阵为：

22、

23、其中，η＝1对应以公比系数递增构建的灰度轴，η＝2对应以等差系数递增构建的灰度轴，η＝3对应以非线性递增构建的灰度轴；

24、步骤3：以某色相颜色值cξ＝(rξ,gξ,bξ)、最高明度节点颜色值cw＝(rw,gw,bw)和最低明度节点的颜色值ck＝(rk,gk,bk)构建奥斯特瓦尔德色立体的各等色相面，各等色相面上色块的三基色混色浓度为：

25、

26、与网格点p(τ,δ,ξ)对应的色块颜色值为：

27、

28、其中，δ＝1,2,...,7,8为等黑度序号，τ＝1,2,...,7,8等白度序号，γ＝1,2,...,7,8为等纯度序号，ωξ,ωw,ωk分别表示三基色的色料重量。

29、可选的，所述步骤2采用以明度等比递增的方法构建灰度轴，所述灰度轴八个节点的混色浓度值矩阵为：

30、

31、其中，

32、

33、所述灰度轴各颜色节点的颜色值为：

34、

35、其中，cw＝[rw,gw,bw]和ck＝[rk,gk,bk]分别表示最高明度和最低明度节点的颜色值。

36、可选的，所述步骤2采用明度等差递增构建奥斯特瓦尔德灰度轴，所述灰度轴八个节点的混色浓度值矩阵为：

37、

38、所述灰度轴各颜色节点的颜色值为：

39、

40、其中，cw＝[rw,gw,bw]和ck＝[rk,gk,bk]分别表示最高明度和最低明度节点的颜色值。

41、可选的，所述步骤2采用明度非线性递增的方法构建灰度轴，所述灰度轴八个节点的混色浓度值矩阵为：

42、

43、所述灰度轴各颜色节点的颜色值为：

44、

45、其中，cw＝[rw,gw,bw]和ck＝[rk,gk,bk]分别表示最高明度和最低明度节点的颜色值。

46、可选的，当ξ＝1,2,...,23,24时，所述奥斯特瓦尔德色立体的等白度面分别为：

47、当τ＝1的等白度面的颜色矩阵为：

48、

49、当τ＝2的等白度面的颜色矩阵为：

50、

51、当τ＝3的等白度面的颜色矩阵为：

52、

53、当τ＝4的等白度面的颜色矩阵为：

54、

55、当τ＝5的等白度面的颜色矩阵为：

56、

57、当τ＝6的等白度面的颜色矩阵为：

58、

59、当τ＝7的等白度面的颜色矩阵为：

60、

61、当τ＝8的等白度面的颜色矩阵为：

62、

63、可选的，当ξ＝1,2,...,23,24时，所述奥斯特瓦尔德色立体的等黑度面分别为：当δ＝1的等黑度面的颜色矩阵为：

64、

65、当δ＝2的等黑度面的颜色矩阵为：

66、

67、当δ＝3的等黑度面的颜色矩阵为：

68、

69、当δ＝4的等黑度面的颜色矩阵为：

70、

71、当δ＝5的等黑度面的颜色矩阵为：

72、

73、当δ＝6的等黑度面的颜色矩阵为：

74、

75、当δ＝7的等黑度面的颜色矩阵为：

76、

77、当δ＝8的等黑度面的颜色矩阵为：

78、

79、可选的，当ξ＝1,2,...,23,24时，所述奥斯特瓦尔德色立体的等纯度面分别为：当γ＝1的等纯度面的颜色矩阵为：

80、

81、当γ＝2的等纯度面的颜色矩阵为：

82、

83、当γ＝3的等纯度面的颜色矩阵为：

84、

85、当γ＝4的等纯度面的颜色矩阵为：

86、

87、当γ＝5的等纯度面的颜色矩阵为：

88、

89、当γ＝6的等纯度面的颜色矩阵为：

90、

91、当γ＝7的等纯度面的颜色矩阵为：

92、

93、当γ＝8的等纯度面的颜色矩阵为：

94、

95、本发明的第二个目的在于提供一种色彩调配系统，用于实现如上述任一项所述的色彩调配方法，所述系统包括：测色设备、奥斯特瓦尔德全色域网格化混色模型构建模块和可视化模块；

96、所述测色设备用于获取实际色料中奥斯特瓦尔德色立体六基色的颜色值；

97、所述奥斯特瓦尔德全色域网格化混色模型构建模块包括：

98、色料颜色值获取模块，被配置为从所述测色设备获取实际色料的颜色值；

99、色相环构建模块，被配置为基于实际获取的奥斯特瓦尔德六基色，构建赤道色相环，给出各色相的颜色值、位置坐标值和混合浓度；

100、灰度轴构建模块，被配置为基于实际获取的黑色和白色分别作为最低明度节点和最高明度节点，构建灰度轴，给出各明度节点的颜色值、位置坐标值和黑色和白色的混合浓度；

101、等色相面色谱构建模块，被配置为构建奥斯特瓦尔德色立体的4εm个等色相面色谱；

102、所述可视化模块，被配置为展示模型色谱，并基于目标色彩的网格点坐标值输出所述六基色对应的混色浓度和颜色值。

103、可选的，所述奥斯特瓦尔德全色域网格化混色模型构建模块还包括：

104、等白度面色谱构建模块，被配置为基于所述4εm个等色相面色谱，将各色相面上白色含量相等的所有网格点构成的圆锥形表面作为奥氏色立体的等白度面；

105、等黑度面色谱构建模块，被配置为基于所述4εm个等色相面色谱，将各色相面上黑色含量相等的所有网格点构成的圆锥形表面作为奥氏色立体的等黑度面；

106、等纯度面色谱构建模块，被配置为基于所述4εm个等色相面色谱，将各色相面上彩色含量相等的所有网格点构成的圆柱形表面作为奥氏色立体的等纯度面。

107、本发明的第三个目的在于提供一种计算机可读存储介质，所述存储介质上存储有计算机程序，当所述计算机程序被处理器执行时，实现如上述任一项所述的方法。

108、本发明有益效果是：

109、1、以获得的红、黄、绿、蓝作为4种彩色色料的主色，以4种主色色料的混合浓度定义网格点的位置，通过二元耦合混色方程获取各网格点的颜色值并构建与经典奥斯特瓦尔德色立体匹配的色相环，解决基于实际颜色获取的色相环分布不均匀的问题，而且可随意设定色相环的色相数，突破了传统的24个色相，因此可以灵活适用于不同调色要求的工业设计场景。

110、2、以实际染色获得的最高明度灰和最低明度灰作为灰度轴的南、北极，获取南、北极颜色值八次等比递增或等比递减的公比系数及灰度轴上8个等级的明度颜色值，以此构建实际的灰度轴，解决理论构建的灰度轴与灰度轴实际明度分布不匹配的问题。

111、3、以实际染色获得的最高明度灰和最低明度灰作为灰度轴的南、北极，在南、北极颜色值之间设计明度值非线性递增函数及灰度轴上8个等级的明度颜色值，以此构建实际的灰度轴，解决理论构建的灰度轴与灰度轴实际明度分布不匹配的问题。

112、4、以实际染色获得的最高明度灰和最低明度灰作为灰度轴的南、北极，在南、北极颜色值之间设计明度值等差递增函数及灰度轴上8个等级的明度颜色值，以此构建实际的灰度轴，解决理论构建的灰度轴与灰度轴实际明度分布不匹配的问题。

113、5、在一种实施方式中，以色相的24个等级、明度的8个等级、纯度的8个等级对奥斯特瓦尔德色立体进行划分，由此获得以8个等白度面、8个等黑度面、24个等色相面组成的奥斯特瓦尔德色立体，并获得各网格点的空间坐标及其对应的混合浓度、颜色值等参数，可通过网格点坐标值获取该网格点对应的基色色料混合浓度及该网格点对应的颜色值。

114、6、在一种实施方式中，以网格点坐标为自变量，分别给出24个等色相面、8个等黑度面、8个等白度面的混合浓度值矩阵及其色谱矩阵。

115、7、在一种实施方式中，基于实际获取的六基色色料颜色值，通过构建的数学模型，以色相为基准获取24个等色相面上的36个色块的颜色值；以黑色色料的混合浓度为基准获取8个等黑度面上的169、145、121、97、73、49、25、1个色块的颜色值；以白色色料的混合浓度为基准获取8个等白度面上的169、145、121、97、73、49、25、1个色块的颜色值。

116、本发明构建的奥斯特瓦尔德全色域网格化混色模型中，每种颜色对应的网格点位置直接关联调配该颜色所需要的黑、白、纯色色料的混合浓度比，因此设计师在调色时可以直接从模型中获取各色料的比例来得到目标颜色，因此极大地提升了设计效率。