一种基于电气距离和功率平衡的配电网两阶段分区方法与流程

本发明涉及智能电网，具体地说是一种基于电气距离和功率平衡的配电网两阶段分区方法。

背景技术：

1、本发明的目的是针对现有技术存在的问题，提供一种基于电气距离和功率平衡的配电网两阶段分区方法。

技术实现思路

1、本发明的目的是通过以下技术方案解决的：

2、一种基于电气距离和功率平衡的配电网两阶段分区方法，其特征在于：该分区电压优化方法步骤为：

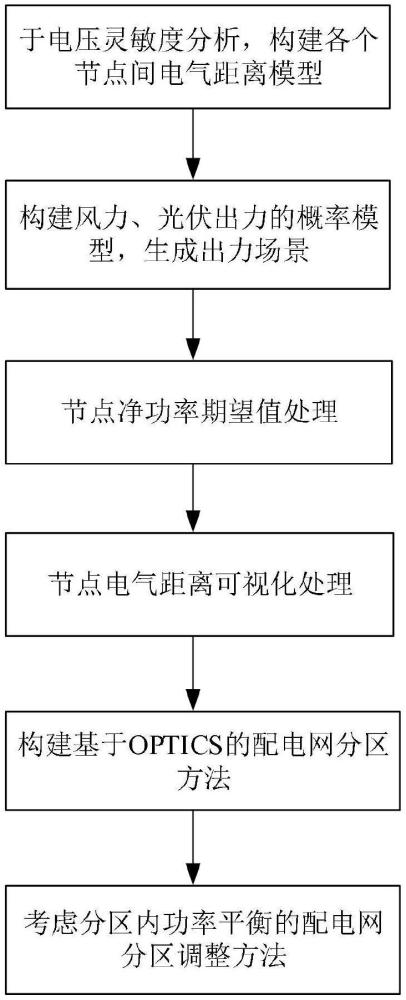
3、a、基于电压灵敏度分析，构建各个节点间电气距离模型；

4、b、构建风力、光伏出力的概率模型，利用蒙特卡洛方法生成多个风电、光伏出力场景及概率分布；

5、c、节点净功率期望值处理模型；

6、d、节点电气距离可视化处理；

7、e、构建基于optics的配电网分区方法；

8、f、考虑分区内功率平衡的配电网分区调整方法。

9、所述步骤a中的基于电压灵敏度分析，构建各个节点间电气距离模型思路为：

10、城市配电网中各个节点之间存在明显的耦合关系。当一个节点的状态量发生改变时，其他节点的状态量或多或少也会发生相应变动。耦合强度受网络支路参数、各节点电压水平和功率影响。分区的目的就是要实现“区内强耦合，区间弱耦合”，以便实现调整区内节点控制量可以明显改善区内其他节点状态量水平，而不会对区外节点产生明显影响，实现区域间解耦调控。

11、极坐标下的牛顿-拉夫逊法的潮流方程如下所示：

12、

13、式中，δθ、δu、δp和δq分别为节点相角、电压、有功和无功的变换量向量，分别为节点单位有功注入和无功注入变化量引起的节点相角的变化量，分别是有功电压灵敏度和无功电压灵敏度

14、

15、节点间耦合强度应由节点间状态量的影响进行反映，节点i和节点j之间的电压灵敏度αi,j表示为；

16、δui＝αi,jδuj (3)

17、式中，δui和δuj分别表示为节点i和节点j的电压变化量。

18、由于配电网的电阻和电抗数量级相当，有功潮流对电压的影响不容忽视，因此采用有功无功综合灵敏度反映电压之间的联系。

19、

20、式中，分别为节点i和节点j之间的由单位有功变化和无功变化产生的电压灵敏度。

21、进一步，由电压灵敏度定义电气距离。电气距离近的节点之间相互影响大，电气距离远的节点之间相互影响小。由于潮流具有方向性，αi,j和αj,i往往不相等。为了消除这种不对称性，同时考虑节点对自身的电气距离为0，定义节点i和节点j之间的电气距离为：

22、di,j＝dj,i＝log(αi,j·αj,i) (5)

23、所述步骤b中的构建风力、光伏出力的概率模型，利用蒙特卡洛方法生成多个风电、光伏出力场景及概率分布的方法为：

24、风力发电功率主要受风速影响，光伏发电功率则与太阳光照强度紧密相关。根据大量风速历史数据统计分析，一定时段内风速大致服从双参数weibull分布，其概率密度函数如式(6)所示：

25、

26、式中：v为风速；k,c为weibull分布的两个参数；vμ和vδ分别为统计时段风速的均值、标准差。

27、风力发电功率pwt与风速v的关系如下所示：

28、

29、式中：vci为切入风速；vco为切出风速；vcr为额定风速；pwt_r为风力发电额定出力。

30、根据大量光伏历史数据统计分析，一定时段内太阳光照强度大致服从beta分布，其概率密度函数为：

31、

32、式中：s为实际光照强度；smax为最大光照强度；α和β为beta分布的两个参数。

33、

34、式中：sμ和sδ分别为统计时段历史晴空因子的均值、标准差。

35、光伏发电功率ppv与光照强度s的关系为：

36、

37、式中：sr为额定光照强度；ppv_r为光伏发电额定出力。

38、根据大量电力负荷历史数据统计分析，一定时段内电力负荷大致服从正态分布，其概率密度函数为:

39、

40、式中，pl为负荷功率；pup,plow分别为负荷的上下限值；pμ和pδ分别为统计时段负荷数据的均值和标准差。

41、建立大规模的系统场景，该系统存在若干状态且服从某种概率分布，对该系统的状态大量随机采样，统计系统模拟的结果计算各指标的均值、方差，分析该系统的不同状态发生的概率，减少计算的复杂性。所述的风速服从双参数weibull分布，太阳光照强度服从beta分布，电力负荷服从正态分布，因此，可随机取样风光荷的状态场景，减小计算的复杂性，提高收敛速度。

42、所述步骤c中的节点净功率期望值处理模型方法为：

43、高比例分布式电源(dg)接入城市配电网后，改变了传统配电网的潮流分布，甚至产生功率倒送现象。因此，在进行配网分区时不仅要考虑节点负荷功率，还要将节点的dg出力纳入计算，采用负荷减去dg出力的净功率作为节点等效负荷。

44、城市配电网中dg多为以可再生分布式电源(rdg),以风电(wt)和光伏(pv)为主。rdg和负荷都存在随机性和波动性，为使短期内分区结果尽量稳定，且能尽量包含系统所有运行工况，采用考虑短期rdg出力预测的电气距离值作为距离度量进行分区。

45、

46、式中，n为分割的场景数目，pk为对应场景的概率。

47、所述步骤d中的节点电气距离可视化处理方法为：

48、电气距离矩阵给出了各个节点之间电气联系的紧密程度，但是无法给出节点之间的相对位置关系，无法直观展示各个节点之间电气距离。非经典多维尺度变换通过节点之间的距离，重构出每个节点的欧几里得坐标，从而可以在二维或者三维坐标系里绘制各个节点。该算法的基本思想是，通过优化的方法，使得重构之后的低维空间中几何表示距离与原样本点之间的距离或者相似性偏离程度尽可能小。其优化的目标函数为：

49、

50、式中，xi为节点i重构出的n维坐标向量，为节点i与j间电气距离期望值。

51、所述步骤e中的基于optics的配电网分区方法为：

52、optics算法是一种基于密度的聚类算法，是对传统密度聚类算法dbscan的一种改进，既继承了密度聚类算法的优点，同时也解决了密度聚类算法参数难以确定的问题。

53、将optics算法应用于配电网分区中存在一些问题。配电网多为辐射状结构，一个节点通常只会连接两三个其他节点，节点之间的连接相对松散。对于结构稀疏的配电网结构来说，原始算法过度关注局部密度，会出现聚类中心过度靠近分区的边缘，聚类中心选择不合理的情况。

54、optics算法的具体步骤如下:

55、初始化：选择适当的参数，如邻域半径ε和最小样本数(minpts)。

56、距离计算：计算每对数据点之间的距离，通常使用欧氏距离或其他合适的距离度量。本文使用以上电气距离模型计算出各节点距离后，利用可视化处理方法，得出各节点的。

57、核心点识别：对每个数据点，统计其在给定邻域半径内的自然邻居数目(即密度)。如果一个数据点的密度大于等于minpts，则将其标记为核心点。

58、可达距离计算：对每个核心点，计算其到其他核心点的可达距离。可达距离是一个核心点到另一个核心点的最小距离。

59、排序：将核心点按照可达距离进行排序，从而形成一个可达性图。

60、聚类识别：通过分析可达性图，找到密度峰值点。这些峰值点表示潜在的聚类中心。聚类的数量可以根据峰值的数量来确定。

61、聚类分配：将数据点分配给聚类，通常是通过遍历可达性图并将数据点分配给最近的密度峰值点来实现。

62、噪声点标记：将未分配给任何聚类的数据点标记为噪声点。

63、结果可视化：根据聚类结果创建可视化，以便理解数据的聚类结构。

64、所述步骤中f的考虑分区内功率平衡的配电网分区调整方法如下：

65、配网分区在保证区域内强耦合，区域间弱耦合的结构基础上，需要进一步满足分区自治的功能。各分区应该尽可能实现有功和无功的功率平衡，减少区域间的能量流动和功率跨区调度，降低网损，提高城市配电网运行经济性。分区内功率平衡也能减轻调度复杂性和通讯压力。采用有功和无功平衡度指标衡量分区的功率平衡情况。

66、无功平衡度指标定义如下：

67、

68、式中，qi为分区i无功平衡度指标，qg为分区内总的无功电源可发最大容量，qd为分区内负荷的总无功需求量；为城市配电网总无功平衡指标，c为分区个数。

69、有功平衡度考虑到光伏出力白天和夜晚的差异，基于日前预测的典型时变场景对其进行描述，具体公式如下：

70、

71、式中，pi为分区i的有功平衡度，pg(t)i和pd(t)分别为分区i在t时刻分布式电源总有功功率和负荷总有功功率，由负荷日前预测值和有功电源的日前调度计划值得到，t为时变场景的计算周期；为城市配电网整体有功功率平衡度指标。

72、综合有功平衡度和无功平衡度，由加权平均得到综合性能指标

73、

74、式中，λp、λq分别为有功和无功平衡度权重系数，满足λp+λq＝1。