基于ME方法的一体化电磁仿真计算方法及系统与流程

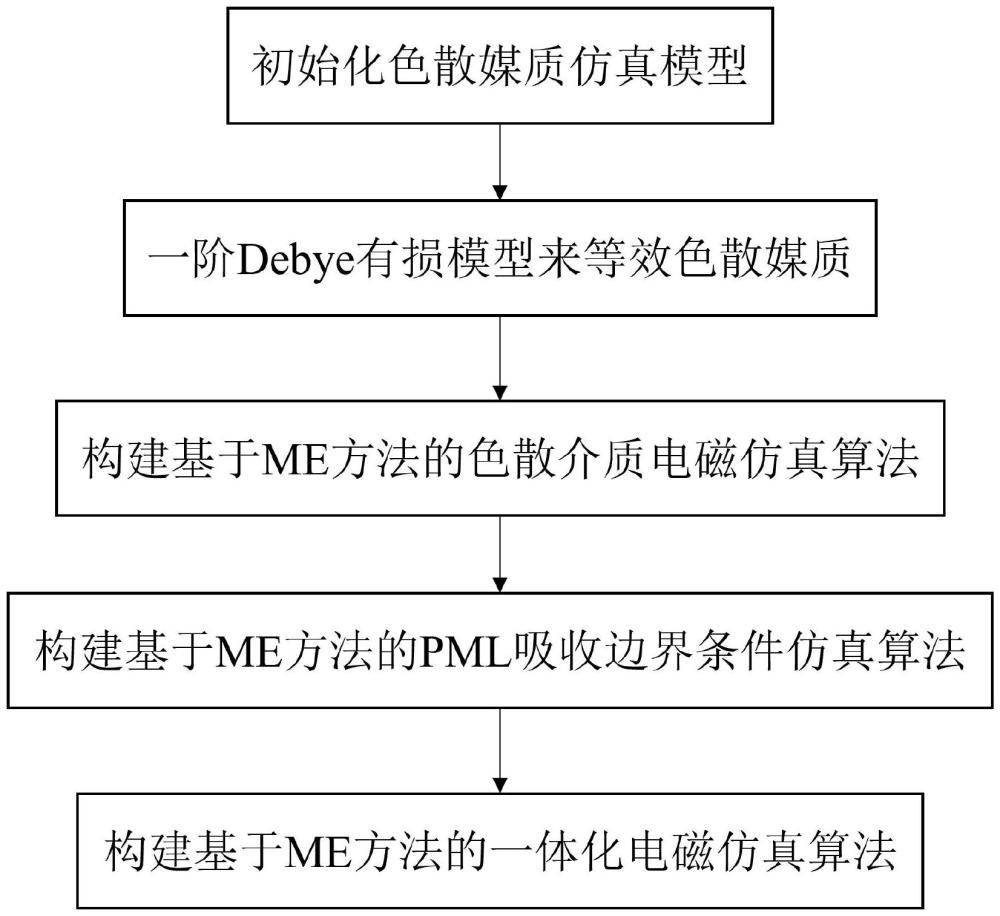
本发明电磁仿真，具体为一种基于me方法的一体化电磁仿真计算方法及系统。

背景技术：

1、近些年来，随着电磁波传输特性的深入研究，它被广泛应用于检测和探测物体。在现有的电磁仿真算法中，时域有限差分方法(fdtd)因为它的实用性和简便性而被广泛使用。对于一般的介质而言，由于其介电常数为定值，所以利用电磁算法进行仿真较为容易。但是针对色散介质而言，由于它的介电常数是随频率变化的，所以传统的fdtd算法无法直接对其进行仿真，需要进行额外处理。随着对色散介质的研究不断深入，可以使用等效模型来代替色散介质，如debye,lorentz,drude等模型，进而使用fdtd算法来推导等效模型的更新方程，进而进行模拟仿真。在对色散介质的仿真中，由于使用fdtd算法仿真物体时需要模拟开放空间，所以需要使用吸收边界条件来截断仿真域。目前最广泛使用的吸收边界条件是复频移完美匹配层(cfs-pml)，它对于传统的分裂pml具有更加简单的更新公式，并且具有更加准确和稳定的参数选择。但是在cfs-pml中由于其具有卷积运算，导致对反射波的吸收效果降低。大部分的色散介质算法和边界条件算法都是单独使用的，并不具有联系性，仿真过程中需要单独对两种算法进行编码，编码复杂度较高。

技术实现思路

1、本发明的目的在于提供一种基于me方法的一体化电磁仿真计算方法及系统，以解决上述背景技术中提出的问题。

2、为实现上述目的，本发明提供如下技术方案：一种基于me方法的一体化电磁仿真计算方法，包括以下步骤：

3、构建色散媒质仿真模型，对模型和边界条件进行区域化预处理；

4、使用一阶debye有损模型来等效色散媒质的电磁特性；

5、使用me方法处理等效模型的麦克斯韦方程组，构建基于me方法的色散介质电磁仿真算法；

6、使用me方法处理无损无耗区域的pml方程，构建基于me方法的pml吸收边界条件仿真算法；

7、基于所述色散介质仿真算法和和所述pml仿真算法，进行公式合并得到基于me方法的一体化电磁仿真算法；

8、使用一体化电磁仿真算法对模型和边界条件区域进行一体化区域更新。

9、优选的，所述一阶debye有损模型为：

10、

11、其中，εr表示相对介电常数，ε∞是无限频率下的介电常数，εs是静态相对介电常数，ε0是空气中的介电常数，τ是弛豫时间，σ是电导率。

12、优选的，所述麦克斯韦方程组为：

13、

14、其中，h和e为磁场和电场；d和b为电位移矢量和磁感应强度。使用debye等效模型处理麦克斯韦方程中的电位移矢量，得到debye等效方程，为

15、

16、其中，d＝ε0εr·e。

17、优选的，所述基于me方法的色散介质电磁仿真算法推导过程包括：

18、将debye等效方程进行拆分之后矩阵化处理，得到一阶矩阵微分方程；

19、对一阶矩阵微分方程进行积分处理，得到解析解；

20、对解析解进行离散处理，得到基于me方法的色散介质电磁仿真算法迭代公式。

21、优选的，所述一阶矩阵微分方程为：

22、

23、其中，

24、f＝(ε0ex ψex1 ψex2 ψex3)t

25、

26、其中，为辅助变量；

27、κ＝ε∞,

28、优选的，所述一阶矩阵微分方程为：

29、

30、其中，n表示时间步。

31、优选的，所述基于me方法的色散介质电磁仿真算法迭代公式为：

32、

33、其中，

34、

35、优选的，所述基于me方法的pml吸收边界条件仿真算法的迭代公式同色散介质迭代公式推导过程一致，为：

36、

37、其中，

38、

39、r″2eη＝r″′2eη·ueη,

40、η＝x,y,z

41、其中

42、η＝x,y,z

43、其中，κη大于等于1，ση和αη大于等于0。

44、优选的，所述基于me方法的一体化电磁仿真算法为：

45、

46、变量的系数矩阵是对色散媒质算法和吸收边界条件算法的进行合并所得到的。

47、一种基于me方法的一体化电磁仿真计算系统，所述系统为基于me方法的一体化电磁仿真计算方法而生成。

48、与现有技术相比，本发明的有益效果是：

49、本申请用于射频与微波器件、人体组织结构等色散介质的模拟仿真中，通过将me-fdtd和me-pml相结合。该算法分别将me方法应用于色散介质fdtd和pml，通过合并和处理这两种算法的公式，将fdtd算法和pml算法结合成更简洁的统一更新公式。该方法不仅减少了使用fdtd算法模拟色散介质时的数值误差，还改善了边界条件对反射波的吸收效果。算法的编码复杂度降低，运行速度提高。

技术特征：

1.一种基于me方法的一体化电磁仿真计算方法，其特征在于，包括以下步骤：

2.根据权利要求1所述的基于me方法的一体化电磁仿真计算方法，其特征在于，所述一阶debye有损模型为：

3.根据权利要求2所述的基于me方法的一体化电磁仿真计算方法，其特征在于，所述麦克斯韦方程组为：

4.根据权利要求3所述的基于me方法的一体化电磁仿真计算方法，其特征在于，所述基于me方法的色散介质电磁仿真算法推导过程包括：

5.根据权利要求4所述的基于me方法的一体化电磁仿真计算方法，其特征在于，所述一阶矩阵微分方程为：

6.根据权利要求4所述的基于me方法的一体化电磁仿真计算方法，其特征在于，所述一阶矩阵微分方程为：

7.根据权利要求4所述的基于me方法的一体化电磁仿真计算方法，其特征在于，所述基于me方法的色散介质电磁仿真算法迭代公式为：

8.根据权利要求1所述的基于me方法的一体化电磁仿真计算方法，其特征在于，所述基于me方法的pml吸收边界条件仿真算法的迭代公式同色散介质迭代公式推导过程一致，为：

9.根据权利要求1所述的基于me方法的一体化电磁仿真计算方法，其特征在于，所述基于me方法的一体化电磁仿真算法为：

10.一种基于me方法的一体化电磁仿真计算系统，其特征在于，所述系统为基于me方法的一体化电磁仿真计算方法而生成。

技术总结本发明公开了一种基于ME方法的一体化电磁仿真计算方法，构建色散媒质仿真模型，对模型和边界条件进行区域化预处理；使用一阶Debye有损模型来等效色散媒质的电磁特性；使用ME方法处理等效模型的麦克斯韦方程组，构建基于ME方法的色散介质电磁仿真算法；使用ME方法处理无损无耗区域的PML方程，构建基于ME方法的PML吸收边界条件仿真算法；基于所述色散介质仿真算法和和所述PML仿真算法，进行公式合并得到基于ME方法的一体化电磁仿真算法；使用一体化电磁仿真算法对模型和边界条件区域进行一体化区域更新。该方法不仅减少了使用FDTD算法模拟色散介质时的数值误差，还改善了边界条件对反射波的吸收效果，算法的编码复杂度降低，运行速度提高。技术研发人员：朱国萃,张旭受保护的技术使用者：安徽黑松科技有限公司技术研发日：技术公布日：2024/11/4