一种重磁位场空间域延拓方法、设备、介质及产品

本发明涉及测试测量领域，特别是涉及一种重磁位场空间域延拓方法、设备、介质及产品。

背景技术：

1、位场向下延拓是增强位场数据的一种有效技术。它通过将位场数据从一个观测面向下延拓至另一个观测面来提高位场数据的分辨率，并突出局部或浅层场源产生的信号。然而，位场向下延拓在数学上是一个不适定问题。为克服位场下延计算固有的不适定性，人们提出了不同类型的位场下延计算方法。根据计算域的不同，现有的位场向下延拓方法大致可分为波数域向下延拓(clarke 1969；et al.2012；zeng et al.2013；zhanget al.2018；tran&nguyen 2020；wang et al.2022)和空间域向下延拓(zhang,wong&lin2016；guo&tao 2020；zuo et al.2020；li et al.2021；zhang et al.2021)两种方式。

2、然而，现有的位场下延方法大多是在波数域中进行计算，在空间域计算的方法相对较少。这是因为在空间域中，人们通常将位场向下延拓建模为求解一个大型线性方程组f＝au，其中，a为方程组系数矩阵，u为待求下延位场的列向量，f为观测数据的列向量(guo&tao2020)。系数矩阵a规模通常较大，在计算机储存需要占用大量的内存空间，一般计算机难以处理。因此许多空间域算法中矩阵向量积运算通常是用波数域fft进行计算(zhang etal.2013；zhang et al.2021)。然而，这种处理方式虽然利用了一些成熟的空间域线性反演算法实现了位场下延，但还是没有发挥空间域位场延拓积分解析解准确的优势。近年来，有学者发现空间域位场延拓系数矩阵具有特殊的bttb矩阵结构，通过将块-循环-循环-块(bttb)矩阵嵌入块-循环-循环-块(bccb)矩阵的方式实现了系数矩阵的矩阵向量积运算(zhang et al.2016)，进而利用线性反演理论实现了较为精确的位场下延计算。zhang etal.(2016)的数值实验结果表明：与基于fft的波数域方法相比，空间域方法在边界附近产生的边界效应很小，且具有更高的精度和鲁棒性。充分展示了空间域延拓方法在位场向下延拓计算中的潜力。虽然目前空间域位场延拓计算的矩阵向量积运算已经得到解决，但大部分研究还是仅限于利用线性反演理论实现空间域位场延拓。

3、除了传统的波数域和空间域下延方法，近年来有学者开始尝试将神经网络技术应用于位场下延计算。chen&yang(2022)构造了一个由多层神经元组成的准神经网络，通过将观测数据作为网络的输入信号，将目标深度的待求下延位场作为输出信号，取得了较好的延拓效果，但该网络单层延拓深度的选取对最终的延拓结果影响较大。ye etal.(2022)提出了一种向下延拓神经网络结构d-unet，利用位场向上延拓计算得到的高海拔平面位场数据作为神经网络的输入，利用深度学习技术有效的映射能力来提高位场病态延拓解的精度。d-unet的延拓精度略优于波数域tikhonov正则化方法，但延拓结果受噪声影响较大。liet al.(2023)设计了一个dc-net网络来计算重力异常向下延拓，网络经过充分训练后，能够较好地恢复重力异常数据的高频细节。但由于训练数据集的海拔高度是固定的，dc-net在延拓距离较大的下延计算中延拓精度会有一定程度的降低。

技术实现思路

1、为解决现有技术存在的上述问题，本发明提供了一种重磁位场空间域延拓方法、设备、介质及产品。

2、为实现上述目的，本发明提供了如下方案：

3、一种重磁位场空间域延拓方法，包括：

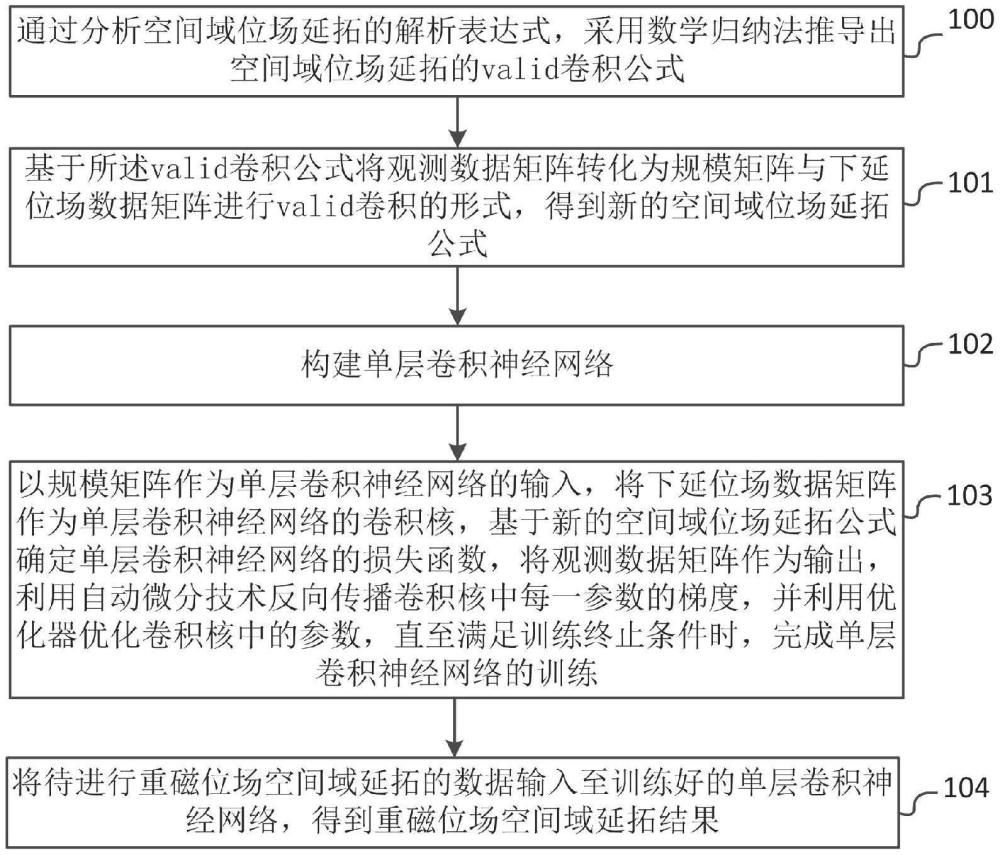
4、通过分析空间域位场延拓的解析表达式，采用数学归纳法推导出空间域位场延拓的valid卷积公式；

5、基于所述valid卷积公式将观测数据矩阵转化为规模矩阵与下延位场数据矩阵进行valid卷积的形式，得到新的空间域位场延拓公式；

6、构建单层卷积神经网络；

7、以所述规模矩阵作为所述单层卷积神经网络的输入，将所述下延位场数据矩阵作为所述单层卷积神经网络的卷积核，基于所述新的空间域位场延拓公式确定所述单层卷积神经网络的损失函数，将所述观测数据矩阵作为输出，利用自动微分技术反向传播卷积核中每一参数的梯度，并利用优化器优化卷积核中的参数，直至满足训练终止条件时，完成单层卷积神经网络的训练；

8、将待进行重磁位场空间域延拓的数据输入至训练好的单层卷积神经网络，得到重磁位场空间域延拓结果。

9、可选地，通过分析空间域位场延拓的解析表达式，采用数学归纳法推导出空间域位场延拓的valid卷积公式，具体包括：

10、在位场解析延拓中，确定高海拔平面数据和低海拔平面数据间满足的关系，得到平面数据关系式；高海拔是指高于设定值的海拔；低海拔是指低于设定值的海拔；

11、采用空间域的数值解法对所述平面数据关系式进行离散化，得到离散化关系式；

12、将所述离散化关系式改写为元素与位场网格化数据中网格数相关的表达式；

13、基于改写得到的表达式，采用数学归纳法推导出空间域位场延拓的valid卷积公式。

14、可选地，所述新的空间域位场延拓公式为：

15、f＝k*vu；

16、式中，f为观测数据矩阵，k为规模矩阵，u为下延位场数据矩阵，*v表示valid卷积。

17、可选地，所述单层卷积神经网络的损失函数表示为：

18、

19、式中，loss为损失函数值，为二范数。

20、可选地，所述优化器为基于梯度的神经网络优化器。

21、可选地，所述规模矩阵是一个维度为2m-1×2n-1的矩阵。

22、一种计算机设备，包括：存储器、处理器以存储在存储器上并可在处理器上运行的计算机程序，所述处理器执行所述计算机程序以实现上述任一项所述的重磁位场空间域延拓方法。

23、一种计算机可读存储介质，其上存储有计算机程序，该计算机程序被处理器执行时实现上述任一项所述的重磁位场空间域延拓方法。

24、一种计算机程序产品，包括计算机程序，该计算机程序被处理器执行时实现上述任一项所述的重磁位场空间域延拓方法。

25、根据本发明提供的具体实施例，本发明公开了以下技术效果：

26、本发明通过分析空间域位场延拓的解析表达式，采用数学归纳法推导出空间域位场延拓的valid卷积公式，并基于valid卷积公式将观测数据矩阵转化为规模矩阵与下延位场数据矩阵进行valid卷积的形式，得到新的空间域位场延拓公式，相较于传统的空间域建模方式，能够大大降低空间域位场延拓模型的复杂度，以大大减少储存需求。并且，本发明构建一种单层卷积神经网络，该网络将规模矩阵作为输入，将下延位场数据矩阵作为卷积核，将观测数据矩阵作为输出，利用深度学习领域的自动微分技术反向传播卷积核每个参数的梯度，同时，利用优化器更新卷积核参数，以完成网络训练，进而使用训练好的网络能够得到精度更高的重磁位场空间域延拓结果。