一种矩阵引导的可解释性时空集成预测方法和系统

本技术涉及地理信息，特别涉及一种矩阵引导的可解释性时空集成预测方法、系统和电子设备。

背景技术：

1、时空预测(spatio-temporal prediction)是地理空间智能(geo-ai)的热门研究主题。该方法结合了时间序列预测和空间分析技术，通过建模时空数据的依赖关系，来推断未来某一时空位置的属性或特征，在环境和气候(例如气象预报)、公共安全(例如犯罪预测)、智能交通(例如交通流量预测)、人类活动(例如人类轨迹模式挖掘)等多个领域有广泛的应用。

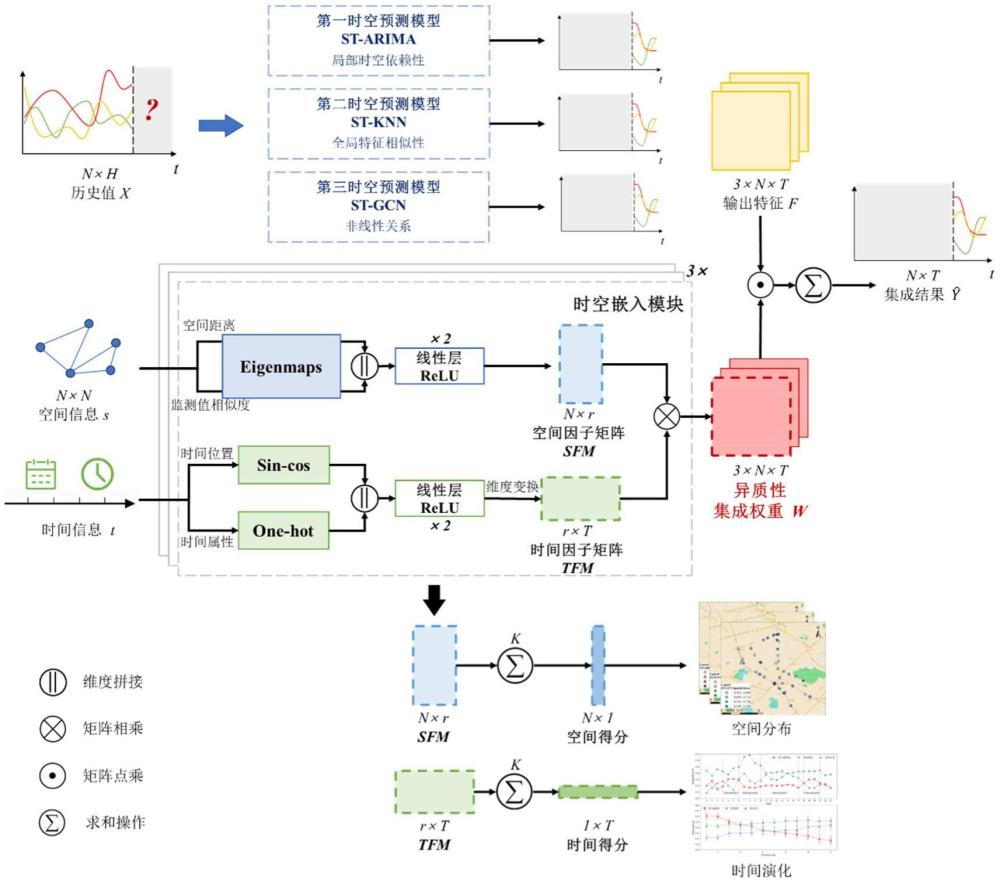
2、为了提高时空预测模型的预测性能和泛化能力，业界将集成学习引入时空数据建模中，通过构建并结合多个异质的基学习器，综合不同单一方法的优点来完成预测任务。这种集成建模策略已被大量文献证明可获得比单一建模策略更强的泛化能力和更高的预测精度。然而，受地理过程动态随机性、地理空间数据时空异质分布的影响，集成学习在时空预测中的应用还存在诸多挑战，限制了其在地学领域中的应用。

3、集成策略的设计主要包括基于统计和基于学习的方法，旨在求解不同基学习器的集成权重。现有研究在设计集成策略时，通常基于样本独立同分布假设，使得不同基学习器的权重在整个时空范围内全局固定。然而，由于地理现象在不同地理位置存在显著差异且随时间动态变化，时空数据表现出明显的空间异质性和时间非平稳性，这使得基于全局的集成策略可能在某些局部时空位置表现不佳。尽管部分现有研究采用地理加权回归模型获得一组基于空间位置的权重来集成不同基学习器的空间预测结果，但对所有时刻共享权重而无法捕捉由时变模式引起的时间非平稳性。此外，部分研究采用k近邻方法给每个时刻的预测样本寻找k个相似的历史样本进行加权预测，但对所有空间位置共享权重而忽略了空间异质性，限制了模型的预测精度。

4、因此，需要提供一种针对上述现有技术不足的改进技术方案。

技术实现思路

1、本技术的目的在于提供一种矩阵引导的可解释性时空集成预测方法、系统和电子设备，以解决或缓解上述现有技术中存在的空间异质性和时间非平稳性的协同表达不足的问题。

2、为了实现上述目的，本技术提供如下技术方案：

3、第一方面，本技术提供了一种矩阵引导的可解释性时空集成预测方法，包括：

4、获取所有空间监测站点的监测值构成的样本的时空状态矩阵；

5、以第一时空预测模型、第二时空预测模型、第三时空预测模型作为集成学习方法的基学习器，将所述时空状态矩阵分别输入所述基学习器，对应得到第一输出特征、第二输出特征、第三输出特征；

6、通过集成策略整合所述第一输出特征、所述第二输出特征、所述第三输出特征，得到最终的集成预测结果；

7、其中，所述集成策略设置有与各个基学习器相对应的、并行的时空嵌入模块，各个所述时空嵌入模块通过非负矩阵分解的方式将各个基学习器的时空异质性集成权重分解成空间因子矩阵和时间因子矩阵的乘积，每一个所述时空嵌入模块设置空间嵌入分支和时间嵌入分支；所述空间嵌入分支用于对监测站点的空间关联信息与所述空间因子矩阵之间的映射关系进行建模，所述时间嵌入分支用于对监测站点的时间属性信息与所述时间因子矩阵之间的映射关系进行建模，进而求解出所述时空异质性集成权重。

8、结合第一方面，可选地，所述第一时空预测模型为时空差分移动平均自回归模型；

9、所述时空差分移动平均自回归模型是在整合移动平均自回归模型的基础上引入空间权重矩阵，通过差分将非平稳的时空状态转化为平稳的时空状态，并将预测变量的历史值以及随机误差项的现值与滞后值进行回归，得到所述第一输出特征。

10、结合第一方面，可选地，所述第二时空预测模型为时空k近邻模型；

11、所述时空k近邻模型是在传统的k近邻方法基础上引入空间信息，将所述时空状态矩阵映射至新的特征空间，在整个历史时间范围内选取特征最相似k个空间邻居进行加权预测，得到所述第二输出特征。

12、结合第一方面，可选地，所述第三时空预测模型为时空图卷积神经网络模型；

13、所述时空图卷积神经网络模型使用图模型建模空间监测站点的非欧几里得结构，采用图卷积操作和门控一维时序卷积gated tcn建模空间和时间维度特征的复杂关联，得到所述第三输出特征。

14、结合第一方面，可选地，所述集成策略采用多元线性回归的集成策略。

15、结合第一方面，可选地，所述空间嵌入分支包括第一编码单元、第一拼接单元和第一学习单元，所述第一学习单元包括两层可学习的网络层，每个网络层包含具有dropout的线性全连接层和relu激活函数；

16、相应地，对监测站点的空间关联信息与所述空间因子矩阵之间的映射关系进行建模，包括如下步骤：

17、所述第一编码单元基于监测站点之间包含的距离和属性相似性，构建图邻近矩阵a，所述图邻近矩阵a包括基于空间欧氏距离的图邻近矩阵和基于监测值相似度的图邻近矩阵

18、第一编码单元根据所述图邻近矩阵a计算拉普拉斯归一化矩阵，并对所述拉普拉斯归一化矩阵进行特征分解，得到特征值矩阵和特征向量；

19、第一编码单元基于所述特征值矩阵、所述特征向量分别构建基于空间欧氏距离的空间嵌入和基于监测值相似度的空间嵌入

20、所述第一拼接单元将基于空间欧氏距离的空间嵌入和基于监测值相似度的空间嵌入进行通道叠加，得到空间嵌入e′s；并将所述空间嵌入e′s输入至所述第一学习单元中，以建立样本空间关联信息和空间因子矩阵的映射关系。

21、结合第一方面，可选地，所述时间嵌入分支包括第二编码单元、第三编码单元、第二拼接单元、第二学习单元，所述第二学习单元包括两层可学习的网络层，每个网络层包含具有dropout的线性全连接层和relu激活函数；

22、相应地，对监测站点的时间属性信息与所述时间因子矩阵之间的映射关系进行建模，包括如下步骤：

23、所述第二编码单元采用三角函数式位置编码对t时刻样本在全局范围的时间位置进行相对编码，得到时间位置嵌入

24、所述第三编码单元选取t时刻样本的m个与集成权重相关的时间属性，并利用一位有效编码方法(one-hot方法)将各个所述时间属性编码为对应的时间属性嵌入1≤j≤m；

25、所述第二拼接单元将所述时间位置嵌入与各个所述时间属性嵌入进行拼接，得到时间嵌入e′t；并将所述时间嵌入e′t输入至所述第二学习单元中，以建立样本时间信息和时间因子矩阵的映射关系。

26、结合第一方面，可选地，还包括：

27、根据空间因子矩阵和时间因子矩阵计算不同时空位置处各基学习器的空间得分向量和时间得分向量；

28、基于所述空间得分向量和所述时间得分向量，分析在空间异质性和时间非平稳性条件下不同基学习器的响应规则。

29、第二方面，本实施例提供一种矩阵引导的可解释性时空集成预测系统，包括：

30、数据获取模块，配置为获取所有空间监测站点的监测值构成的样本的时空状态矩阵；

31、基学习器模块，配置为以第一时空预测模型、第二时空预测模型、第三时空预测模型作为集成学习方法的基学习器，将所述时空状态矩阵分别输入所述基学习器，对应得到第一输出特征、第二输出特征、第三输出特征；

32、集成模块，配置为通过集成策略整合所述第一输出特征、所述第二输出特征、所述第三输出特征，得到最终的集成预测结果；

33、其中，所述集成策略设置有与各个基学习器相对应的、并行的时空嵌入模块，各个所述时空嵌入模块通过非负矩阵分解的方式将各个基学习器的时空异质性集成权重分解成空间因子矩阵和时间因子矩阵的乘积，每一个所述时空嵌入模块设置空间嵌入分支和时间嵌入分支；所述空间嵌入分支用于对监测站点的空间关联信息与所述空间因子矩阵之间的映射关系进行建模，所述时间嵌入分支用于对监测站点的时间属性信息与所述时间因子矩阵之间的映射关系进行建模，进而求解出所述时空异质性集成权重。

34、第三方面，本实施例提供一种计算机可读存储介质，其上存储有计算机程序，所述计算机程序被处理器执行时实现如上任一实施例所述的矩阵引导的可解释性时空集成预测方法。

35、第四方面，本实施例提供一种电子设备，包括：存储器、处理器、以及存储在所述存储器中并可在所述处理器上运行的程序，所述处理器执行所述程序时实现如上任一实施例所述的矩阵引导的可解释性时空集成预测方法。

36、本技术实施例的技术方案具有如下有益效果：

37、本实施例的技术方案中，集成学习方法的基学习器包括三个基学习器，在集成策略中设置与各个基学习器相对应的、并行的时空嵌入模块，并在每个时空嵌入模块设置空间嵌入分支和时间嵌入分支，先由各个时空嵌入模块采用非负矩阵分解的方式将基学习器各自的时空异质性集成权重分解成空间因子矩阵和时间因子矩阵的乘积，再通过空间嵌入分支对监测站点的空间关联信息与空间因子矩阵之间的映射关系进行建模，求得空间因子矩阵中各个元素的值，通过时间嵌入分支对监测站点的时间属性信息与时间因子矩阵之间的映射关系进行建模，求得时间因子矩阵中各个元素的值，进而将空间因子矩阵和时间因子矩阵相乘，求解出时空异质性集成权重，再利用该时空异质性集成权重对三个基学习器的输出特征进行整合，得到最终的集成预测结果。该方案将矩阵分解和集成学习进行融合，以两个因子矩阵(即空间因子矩阵和时间因子矩阵)的求解过程为引导，实现集成过程空间异质性和时间非平稳性的协同精确表达。