一种基于砂体构型约束的致密砂岩储层裂缝定量预测方法

本发明属于石油天然气勘探与开发，具体涉及一种基于砂体构型约束的致密砂岩储层裂缝定量预测方法的设计。

背景技术：

1、致密砂岩油气资源在全球范围内分布广泛，储量巨大。北美地区、中国、中东等地的致密砂岩油气的发现，都充分证明了致密砂岩油气资源在全球能源领域具有巨大的潜力，这些资源的开发利用，可以为全球能源供应提供新的来源，有助于缓解能源紧张局面，促进经济的稳定发展。但较常规天然气资源而言，致密砂岩储层物性较差，通常具有低孔、低渗的特性，使得其油气资源的开采难度较大。然而，裂缝的发育可以大大改善储层的物性条件，为油气资源的储存和运移提供了良好的空间。裂缝通过连通孤立的孔洞，构建了一个更为连续和有效的储集空间，不仅提高了含气饱和度，还为油漆的储存提供了更多的可能性。裂缝还使得油气能够沿裂缝通道更容易地流动和聚集，从而提高基质的渗透率，使得储层中的油气资源更容易被开采出来。一个发育良好的裂缝网络不仅能够显著提高储层的油气储存能力，还能够保证在开采过程中油气资源能够稳定、高效地流出。因此，裂缝发育程度被认为是评估致密砂岩储层能否获得高产及稳产的关键因素。

2、然而，裂缝的发育也受多种因素的影响，目前，关于裂缝的发育特征和分布规律的主控因素研究主要集中在岩性、岩相、岩层厚度、构造、应力等。但砂体构型界面控制下的储层非均质性也是影响储层裂缝发育和分布的关键因素，尤其是在构造差应力值较小的地区，它甚至可能成为控制裂缝发育的主导因素，由于构型界面上下岩层沉积物粒度变化、组分和力学性质存在差异，容易产生应力集中和分布不均的现象，构型界面附近往往成为应力集中的区域，更容易形成裂缝。因此，在油气勘探和开发过程中，需要充分考虑储层内部砂体构型界面对储层裂缝的控制作用，以便更准确地预测裂缝的发育和分布情况，为致密砂岩储层油气资源的开发和利用提供有力支持。

技术实现思路

1、本发明的目的是为了解决现有致密砂岩储层裂缝定量预测方法存在诸多局限性的问题，提出了一种基于砂体构型约束的致密砂岩储层裂缝定量预测方法。

2、本发明的技术方案为：一种基于砂体构型约束的致密砂岩储层裂缝定量预测方法，包括以下步骤：

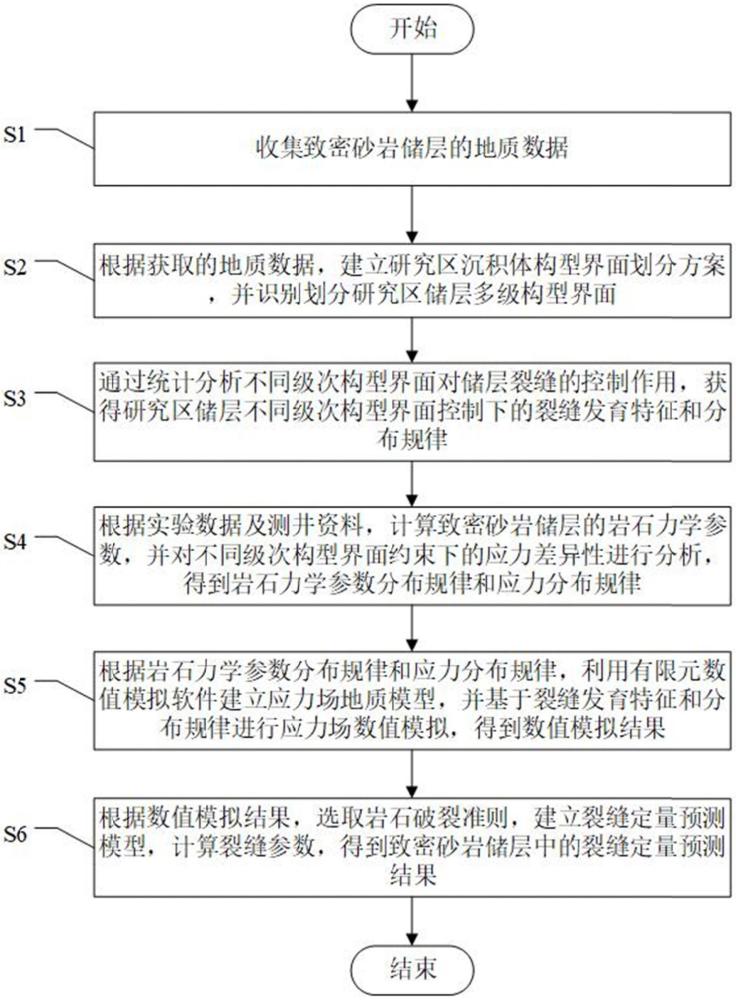
3、s1.收集致密砂岩储层的地质数据；

4、s2.根据获取的地质数据，建立研究区沉积体构型界面划分方案，并识别划分研究区储层多级构型界面；

5、s3.通过统计分析不同级次构型界面对储层裂缝的控制作用，获得研究区储层不同级次构型界面控制下的裂缝发育特征和分布规律；

6、s4.通过实验测试及测井资料，计算致密砂岩储层的岩石力学参数，并对不同级次构型界面约束下的应力差异性进行分析，得到岩石力学参数分布规律和应力分布规律；

7、s5.根据岩石力学参数分布规律和应力分布规律，利用有限元数值模拟软件建立应力场地质模型，并基于裂缝发育特征和分布规律进行应力场数值模拟，得到数值模拟结果；

8、s6.根据数值模拟结果，选取岩石破裂准则，建立裂缝定量预测模型，计算裂缝参数，得到致密砂岩储层中的裂缝定量预测结果。

9、本发明的有益效果是：

10、1.该方法通过引入砂体构型约束，结合野外、岩心等地质资料和成像测井技术，能够全面揭示致密砂岩储层裂缝的发育特征，这包括裂缝的产状、规模、分布规律以及裂缝间的连通性等，也能够精准地揭示致密砂岩储层中应力的分布规律，明确裂缝形成的力学机制，为裂缝的定量预测提供了更为科学的依据。

11、2.通过本发明准确预测裂缝分布，可以减少不必要的钻探和测试工作，降低勘探开发成本。

12、作为优选，步骤s2中所述的研究区沉积体构型界面划分方案将研究区沉积体构型划分为1级构型界面、2级构型界面、3级构型界面、4级构型界面和5级构型界面；所述1级构型界面为单一岩相的界面，为纹层组构成的层系与层系之间的界面，底部无侵蚀，在岩心上通过交错前积层的削蚀或尖灭来识别；所述2级构型界面为单一岩相的叠加界面，为层系组与层系组之间的界面，层系组由多个岩性相似或成因有联系的层系叠加构成，底部无侵蚀，界面上下有岩相的变化；所述3级构型界面为巨型底型内的侵蚀面，其倾角小于15°，界面上泥质含量增加，见碎屑泥砾，界面上下岩相组合相似；所述4级构型界面为巨型底型的界面，即单一河道的界面，以滞留沉积与冲刷面识别，为岩相组合变化、沉积微相变化的界面；所述5级构型界面为同期河道叠置砂体的界面，以切割-充填底型及底部滞留砾石为标志，为沉积相变化的界面。

13、上述优选方案的有益效果是：

14、通过将研究区沉积体构型划分为五级构型界面的划分方案并结合岩心以及测井数据来识别划分出研究区不同单井的沉积相和多级砂体构型界面，进而明确了不同级次构型界面对裂缝发育的控制作用。

15、作为优选，步骤s4中所述岩石力学参数包括杨氏模量、剪切模量、泊松比、抗拉强度、抗压强度、体积压缩模量和内摩擦角。

16、上述优选方案的有益效果是：

17、岩石力学参数是用于描述岩石在受力状态下的力学性质的参数，通过对各岩石力学参数的研究，能够全面揭示致密砂岩储层裂缝的发育特征，同时也能够精准地揭示致密砂岩储层中应力的分布规律，明确裂缝形成的力学机制。

18、作为优选，所述步骤s4具体包括以下步骤：

19、s41.通过实验测试及测井资料，计算得到杨氏模量和泊松比；

20、s42.根据杨氏模量和泊松比计算得到所有岩石力学参数，并基于不同的沉积微相统计分析得到研究区不同级次构型界面下岩石力学参数分布规律；

21、s43.基于研究区重点井测井数据及岩石力学参数，选择最优计算模型，并进行应力计算，得到单井应力状态；

22、s44.根据单井应力状态，通过属性建模得到应力数据体，并得到应力分布规律。

23、作为优选，步骤s41中所述杨氏模量计算公式为：

24、

25、所述泊松比计算公式为：

26、

27、其中，e为杨氏模量，μ为泊松比，ρb为岩石密度，δtp表示纵波时差，δts表示横波时差。

28、作为优选，步骤s43中所述应力计算包括垂向地应力计算和水平地应力计算；所述垂向地应力计算公式为：

29、

30、所述水平地应力计算公式为：

31、

32、其中，σv为垂向应力，ρ(h)为地层密度与深度之间的函数，h为最大地层深度，g为重力加速度，h为地层深度，σh为水平最大主应力，σh为水平最小主应力，μ为泊松比，pp为地层孔隙压力，α为有效应力系数，ξ1、ξ2为地层构造应力影响系数。

33、上述优选方案的有益效果是：

34、通过对岩石力学参数和单井应力状态进行计算，明确岩石力学参数分布规律和应力分布特征，为裂缝的定量预测提供了更为科学的依据。

35、作为优选，步骤s6中所述裂缝参数包括岩石破裂应力、弹性模量、裂缝应变能密度、裂缝开度、裂缝表面能、裂缝体积密度、裂缝线密度、裂缝倾角和最大弹性张应变。

36、作为优选，所述岩石破裂应力的计算公式为：

37、

38、其中，σp为岩石破裂应力，c0为内聚力，为内摩擦角；

39、所述弹性模量的计算公式为：

40、e＝e0σp

41、其中，e为弹性模量，e0为与岩性有关的比例系数；

42、所述裂缝应变能密度的计算公式为：

43、

44、其中，wf为裂缝应变能密度，w为应变能密度，we为新增单位裂缝表面积必须克服的应变能，σ1为最大有效主应力，σ2为中间有效主应力，σ3为最小有效主应力，μ为泊松比；

45、所述最大弹性张应变的计算公式为：

46、

47、其中，ε0为最大弹性张应变；

48、所述裂缝开度的计算公式为：

49、低角度缝和网状缝：

50、高角度缝(>70°)：

51、其中，d为裂缝开度，rd为深侧向电阻率，rb为基岩块电阻率，kr为浅侧向畸变系数，rs为浅侧向电阻率，rm为钻井液电阻率；

52、所述裂缝表面能的计算公式为：

53、j＝j0+δj＝j0+σ3d

54、其中，j为裂缝表面能，j0为零围压时裂缝表面能，δj为裂缝表面能的变化量；

55、所述裂缝体积密度的计算公式为：

56、

57、其中，dvf为裂缝体积密度。

58、作为优选，所述裂缝线密度的计算公式为：

59、

60、其中，d1f为裂缝线密度，kf为裂缝渗透率，φf为裂缝孔隙度；

61、所述裂缝倾角的计算公式为：

62、

63、其中，y为裂缝倾角，y<0表示裂缝倾角小于30°，0<y<0.1表示裂缝倾角大于30°小于70°，y>0.1表示裂缝倾角大于70°，rd为深侧向电阻率，rs为浅侧向电阻率。

64、作为优选，所述裂缝线密度的计算公式为：

65、

66、其中，dvf为裂缝体积密度，l1为沿主应力方向σ1的单元长度，l3为沿主应力方向σ3的单元长度，θ为破裂角。

67、上述优选方案的有益效果是：

68、通过对各裂缝参数进行计算，实现了对裂缝的定量预测，并且减少了不必要的钻探和测试工作，降低勘探开发成本。