一种基于事件触发博弈策略的多智能体系统编队控制方法
- 国知局
- 2024-12-06 12:11:24
本发明涉及智能体编队控制领域,特别涉及一种基于事件触发博弈策略的多智能体系统编队控制方法。
背景技术:
1、多智能体系统的编队控制在多机器人和无人机协同等方面有着广泛的应用。通过多智能体系统的编队控制可以实现智能体间良好的组织结构,从而良好地实现整体性能。通过协同工作,可以完成单个智能体难以完成的复杂任务。
2、现有的多智能体系统的编队控制主要通过领导者-跟随者法、虚拟结构法、人工势场法等。这些方法往往侧重于静态或预设条件下的编队控制。然而,在实际应用中,多智能体系统往往需要面对复杂多变的环境和不确定性的任务需求,这就需要一种更加灵活、智能且能够适应动态变化的编队控制方法。博弈论作为研究理性智能体之间策略交互的数学理论与方法,为解决这类问题提供了新的视角和工具。
3、利用博弈论的理论框架,智能体之间进行策略交互,追求自身利益最大化或代价成本的最小化,并考虑与其他智能体间的合作竞争关系,这种系统通常能在复杂环境中做出更合理的决策。针对多智能体系统,z.deng.等人给出一种基于博弈论的高阶系统编队控制方法,然而,只考虑了智能体间的“合作”关系,很多情形下,智能体间不止存在“合作”的关系,“合作”和“竞争”同时存在的关系也不容忽视。另外,智能体间的信息传输被假定是连续的,该方法在通信资源有限的情况下可能受限,且期望队形是在无穷时刻达到的,这不利于工程实际应用。
技术实现思路
1、为解决上述技术问题,本发明提供了一种基于事件触发博弈策略的多智能体系统编队控制方法,用以解决现有技术中通信资源有限及收敛时间过长的问题,并通过博弈策略算法实现复杂系统中的智能决策。
2、为达到上述目的,本发明的技术方案如下:
3、一种基于事件触发博弈策略的多智能体系统编队控制方法,包括如下步骤:
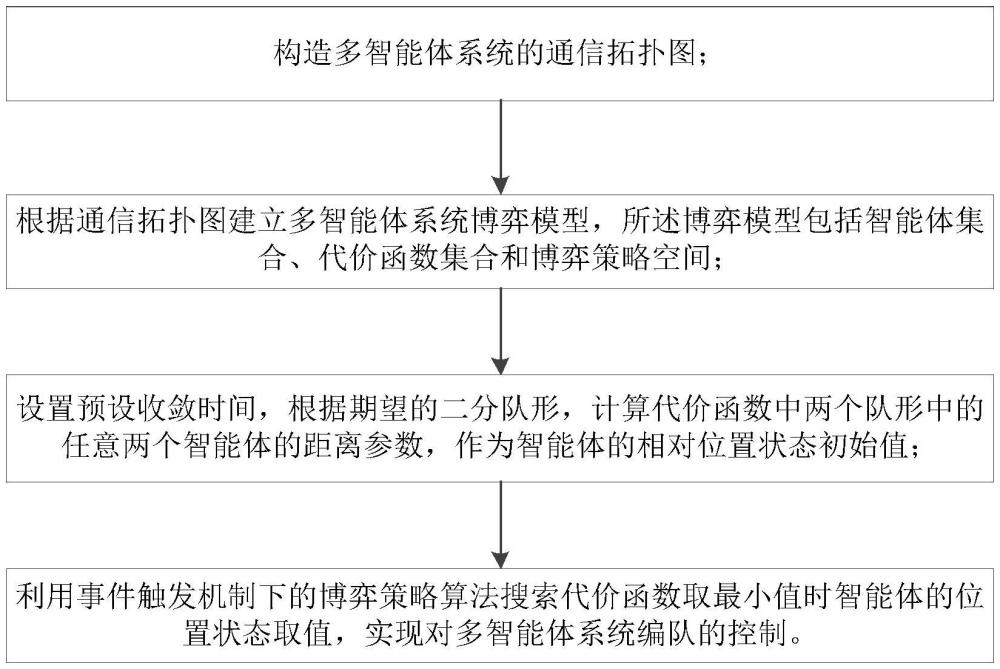
4、步骤1,构造多智能体系统的通信拓扑图;
5、步骤2,根据通信拓扑图建立多智能体系统博弈模型,所述博弈模型包括智能体集合、代价函数集合和博弈策略空间;
6、步骤3,设置预设收敛时间,根据期望的二分队形,计算代价函数中两个队形中的任意两个智能体的距离参数,作为智能体的相对位置状态初始值;
7、步骤4,利用事件触发机制下的博弈策略算法搜索代价函数取最小值时智能体的位置状态取值,实现对多智能体系统编队的控制。
8、上述方案中,步骤1中,构造的通信拓扑图表示为g={v,e,a},其中,v代表智能体集合,即通信拓扑图中的节点集合;代表边集合,边(j,i)表示智能体i能接收智能体j的信息,并称j是i的邻居;
9、a=[aij]∈rn×n表示邻接加权矩阵,aij是邻接加权矩阵a的第i行第j列元素,即智能体j指向智能体i的边的边权重,rn×n表示n行n列的实数矩阵,
10、若边权重aij>0,表示智能体i和j是合作关系;若边权重aij<0,则表示智能体i和j是竞争关系;
11、如果对于任意的边权重,都有aij=aji成立,则通信拓扑图g是无向的;若通信拓扑图g中任意两个节点均有一条通路,则称通信拓扑图g是连通的;
12、若存在两个节点集合v1,v2满足v1∪v2=v及对于节点集合v中的任意两个智能体i和j,满足如下条件的通信拓扑图g是结构平衡的:若vi,vj∈v1或者vi,vj∈v2成立,则有aij≥0成立;若vi∈v1,vj∈v2或者vi∈v2,vj∈v1成立,则有aij≤0成立;所构造的智能体间的拓扑结构是无向连通且结构平衡的。
13、上述方案中,步骤2中,建立的多智能体系统博弈模型表示为ω={v,j,s};
14、其中,v={v1,v2,...,vn}为智能体集合,v1,v2,...,vn分别表示第1,2,...,n个智能体,以下将第i个智能体vi简称智能体i,参数i∈{1,2,...,n};
15、j={j1,j2,...,jn}是代价函数集合,j1,j2,...,jn分别表示第1,2,...,n个智能体的代价函数;
16、s=s1×s2×...×sn表示博弈策略空间,s1,s2,...,sn分别表示第1,2,...,n个智能体的博弈策略。
17、上述方案中,步骤2中,所述代价函数为:
18、
19、其中,ni表示智能体i的邻居集合;xi表示智能体i的位置状态;xj表示智能体j的位置状态;x表示所有智能体位置状态的集合;ji(x)表示与x有关的智能体i的代价函数;sign()表示符号函数;di、dj是智能体i和j的距离参数,两智能体相对距离dij=di-dj;表示预设函数μ(t)的一阶导数,μ(t)为t时刻下的预设函数,定义为:
20、
21、其中,t表示预设收敛时间,且t>0;α表示收敛参数,且0<α≤1。
22、上述方案中,步骤3中,节点集合v1,v2分别构成两个队形,需要分别计算两个队形的对应参数;
23、di、dj的计算方法如下:以二维平面编队为例,需对横纵坐标分别进行解算;
24、首先,计算集合v1构成的期望队形中的两个智能体i和j的横坐标之间的相对距离dij;
25、根据dij=di-dj可以得到不同的i和j取值下的方程组,由此得到方程组的任意一组解,即可解得代价函数中的距离参数di、dj;
26、同理,对于集合v1构成的期望队形中的两个智能体i和j的纵坐标距离参数也可解得;
27、集合v2中智能体的距离参数按照相同方法计算;由此,整个系统的距离参数di、dj根据期望的二分队形计算得出。
28、上述方案中,步骤4的具体方法如下:
29、(1)系统初始化;
30、(2)运行博弈策略算法,同时,执行事件检测处理过程,判断是否满足触发条件,若满足,则更新系统采样状态和控制信号,若不满足,则不更新;
31、(3)重复上述事件检测处理过程,直至形成期望的二分队形。
32、进一步的技术方案中,步骤(1)中,系统初始化包括所有智能体初始位置状态的初始化,即在t=0时刻下x1,x2,...,xn的取值,该初始状态的取值为任意实数;
33、代价函数中参数的初始化,包括与智能体i和j的相对距离dij有关的距离参数di、dj,预设收敛时间t、收敛参数α;
34、博弈策略算法参数的初始化,包含控制增益ki,动态变量ηi(t)的初始值ηi(0),动态变量的指数项m,触发条件参数β1i、β2i、β3i。
35、进一步的技术方案中,步骤(2)中,博弈策略算法为:
36、
37、其中,表示智能体i的位置状态xi的一阶导数;ki表示控制增益,且ki>0;ji表示智能体i的代价函数;
38、yi=[yi1,yi2,...,yin]t,yi表示智能体i对其他智能体的状态估计,向量yi中的元素yij为智能体i对j的状态估计,其模型为:
39、
40、其中,表示智能体i在时间t之前的上一采样时刻yij的状态,同理,表示智能体k在时间t之前的上一采样时刻ykj的状态;aik表示智能体k指向智能体i的边的边权重,表示预设函数μ(t)的一阶导数,ni表示智能体i的邻居集合。
41、进一步的技术方案中,步骤(2)中,触发条件如下:
42、
43、其中,触发条件参数β2i>0、β3i>0,均为正常数;
44、aij表示智能体j指向智能体i的边的边权重,表示智能体i的采样状态,表示智能体j的采样状态,(ex)i表示智能体i的采样状态与实时状态xi的差值,(ey)i表示智能体i的采样状态与实时状态yi的差值,
45、动态变量为触发条件中设置的一个变量,它在t时刻的定义为:
46、
47、其中,m是动态变量的指数项,取值范围为m>0;
48、智能体i在t时刻的动态变量ηi(t)在t时刻的动态为:
49、
50、其中,动态变量ηi(t)是触发条件中设置的一个动态变量,其目的是避免芝诺行为,它的初始值ηi(0)>0。
51、通过上述技术方案,本发明提供的一种基于事件触发博弈策略的多智能体系统编队控制方法具有如下有益效果:
52、1、本发明通过事件触发控制的引入,能够节约大量通信资源,适用于通信资源受限的情形,更符合工程实际。
53、2、本发明通过预设函数的引入,实现了预设收敛时间内的二分编队控制。
54、3、本发明通过设置边权重符号,边权重为正表示合作关系,边权重为负表示竞争关系,考虑了智能体的合作竞争关系,应用范围更加广泛。
本文地址:https://www.jishuxx.com/zhuanli/20241204/339862.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请发送邮件至 YYfuon@163.com 举报,一经查实,本站将立刻删除。