一种基于成熟度理论的大体积混凝土早期开裂指数及其时空分布预测方法

本发明涉及大体积混凝土开裂指数及其时空分布计算方法，属于建筑结构分析计算。

背景技术：

1、随着我国在水利、建筑和交通等大型基础设施上的投入不断增加，大体积混凝土的应用越来越普遍。然而，在早期阶段，混凝土由于水化反应产生大量水化热，导致内部温度剧烈变化。这种温度变化容易引发温度收缩变形，从而导致开裂。裂缝不仅影响建筑物的外观，还会降低结构构件的承载能力，并可能导致渗漏、钢筋锈蚀、混凝土碳化加速和强度降低等问题，严重时甚至可能危及建筑物的正常使用寿命。因此，早期阶段的开裂指数及其时空分布计算在大体积混凝土结构的设计和施工中具有重要意义。

2、在大体积混凝土结构中最具代表性的体积变形包括：(1)胶凝材料水化反应放热引起的温度变形；(2)胶凝材料水化反应导致水分消耗产生的收缩变形。目前，国内外学者关于温度开裂方面的数值模拟中所用热源函数主要是基于绝热温升试验转化过来的反应放热，无法真实的反映混凝土的实际放热。此外，以往研究大多只涉及到温度场计算，有关开裂驱动力、抗拉强度、弹性模量等参数的计算均未涉及空间的概念。此外，大体积混凝土不同点的温度演化历史不同，使得同一时刻不同位置混凝土的水化度不同，因此必须采用成熟度理论计算混凝土空间上各部位的性能发展。目前，通常采用“开裂风险”来评估大体积混凝土是否开裂，但实际上开裂风险是若干开裂指数的概率密度。因此，本发明统一采用“开裂指数”及其时空分布来评估大体积混凝土的开裂可能性。为提高大体积混凝土开裂指数及其时空分布的计算精度，本发明测试了20℃、40℃、60℃和80℃下的胶凝材料反应热、及混凝土抗拉强度、弹性模量和孔隙率，通过孔隙率测试结果修正了高温损伤下的抗拉强度和弹性模量，并基于成熟度理论和时空分布计算了大体积混凝土的温度场、温度应变场、收缩应变场、弹性模量场、应力场和抗拉强度场，同时引入了松弛系数以考虑徐变对应力的影响，提高了大体积混凝土开裂指数及其时空分布预测的精确度。

技术实现思路

1、本发明要解决的技术问题是，针对目前大体积混凝土开裂指数及其时空分布计算无法同时考虑时变、温变和空间位置不同从而水化反应放热、力学性能和收缩变形不同的影响，提供了一种基于成熟度理论的大体积混凝土早期开裂指数及其时空分布预测方法，结果更为准确可靠。

2、本发明为解决上述技术问题所采用的技术方案为：一种基于成熟度理论的大体积混凝土早期开裂指数及其时空分布预测方法，包括以下步骤：

3、步骤一，在abaqus中建立大体积混凝土的实体模型，混凝土的尺寸为76.1m×74.1m×5.5m，混凝土等级为c50；

4、步骤二，进行网格划分，选用dc3d8热传导立方体单元，在计算过程由于网格划分个数较多，选用了减缩积分；

5、步骤三，建立热传导方程，中的热源函数其中，q为单位时间单位体积中发出的热量，j/(m3·h)；c为比热容，j/(kg·℃)；ρ为混凝土密度，kg/m3；m为单位体积混凝土中胶凝材料用量，kg/m3；q为单位质量胶凝材料在单位时间内的放热量，j/(kg.h)；q’为单位质量胶凝材料的放热量，j/kg；

6、步骤四，建立成熟度理论的方程：

7、其中q’(t,t’)为单位质量胶凝材料t时刻受温度影响的放热量；a是指前因子；r为气体常数，8.314j/(mol·k)；t’是恒温温度，℃；ea为活化能，j/mol，t为龄期；t0是初始时间；，；q’max为t→∞时混凝土胶凝材料的累计放热；

8、步骤五，设定温度场边界条件和初始条件；

9、步骤六，混凝土温度应变的表达式为dεt＝αt·dt，其中εt是温度应变，αt是热膨胀系数，dt为温度增量；

10、步骤七，混凝土的早期收缩应变εw可通过下式计算：

11、

12、其中，η为刚度影响系数，c50混凝土取9.5×10-3；α为水化度；w/c为水胶比，ρc和ρw分别为粉体和水密度；m为水的摩尔质量；r为气体常数；t为温度；k为含孔材料的体积模量；ks为不含孔材料的体积模量为44gpa；其中，k＝e/3(1-2v)，e为弹性模量；ρ为水的密度；v为泊松比0.209；rhin为混凝土内部相对湿度；vp为孔隙总体积；

13、步骤八，水化程度α(t,t)通过下式得到：ms(t,t’)根据下式求得其中m1(t,105℃)为样品在时间t时处于105℃的质量；m2(t,950℃)为样品在时间t时处于950℃的质量；mcar(t,600～750℃)为样品在时间t时处于600℃～750℃的质量；msmax为完全水化样品的结合水量；

14、步骤九，实际上，混凝土材料并不是严格地服从虎克定律，其应力-应变关系不严格符合σ＝e·ε的线性关系，松弛应力与弹性应力之间的关系表达式为：σrelax(t，τ)＝σelas(τ)ψ(t，τ)，其中σrelax(t,τ)为松弛应力，σelas(t,τ)为弹性应力，ψ(t,τ)为松弛系数，τ为混凝土的终凝时间；

15、步骤十，混凝土开裂指数及其时空分布计算式为

16、式中，η(t,t,x,y,z)＝是t时刻受温度影响的混凝土内部任意点的开裂指数；σelax(t,τ,t,x,y,z)为t时刻受温度影响的混凝土内部任意点变形拉应力(开裂驱动力)，mpa；ψ(t,τ,t,x,y,z)为松弛系数；ft(t,t,x,y,z)为t时刻受温度影响的混凝土内部任意点自身抗拉强度(开裂抗力)，mpa；e(t,t,x,y,z)为混凝土t时刻受温度影响的混凝土内部任意点弹性模量，mpa；εs为混凝土t时刻受温度影响的混凝土内部任意点收缩应变；εt为混凝土t时刻受温度影响的混凝土内部任意点温度应变；r为约束度，嵌固基础底板结构近似为1。

17、基于恒温条件下测得的4个温度下胶凝材料反应热，采用非线性最小二乘法计算得到3个未知参数q’max、a和ea。

18、依据步骤八的计算过程求得不同时刻不同温度下的水化度。

19、为避免大体积混凝土降温过快导致开裂，通常为密闭不失水环境，一直处于湿度饱和期；为此，在水浴恒温环境条件下测得4个温度下的混凝土收缩应变，以验证计算结果的正确性。

20、松弛系数为而徐变系数通过下式计算：

21、其中α(t,t)为受时间和温度共同影响的水化程度；ω为水胶比；n为松弛因子，其值根据王铁梦推荐的经验取为0.3；d为常数，其为0.35；τ为混凝土的终凝时间；t为温度。

22、由于高温水化快，形成的浆体结构较为疏松导致强度低，因此，本发明以70℃为临界损伤温度，基于高温下孔隙率的测试结果，引入损伤因子得到考虑高温损伤的混凝土弹性模量和抗拉强度：

23、e＝e0-ζφ；ft＝ft0-ζφ

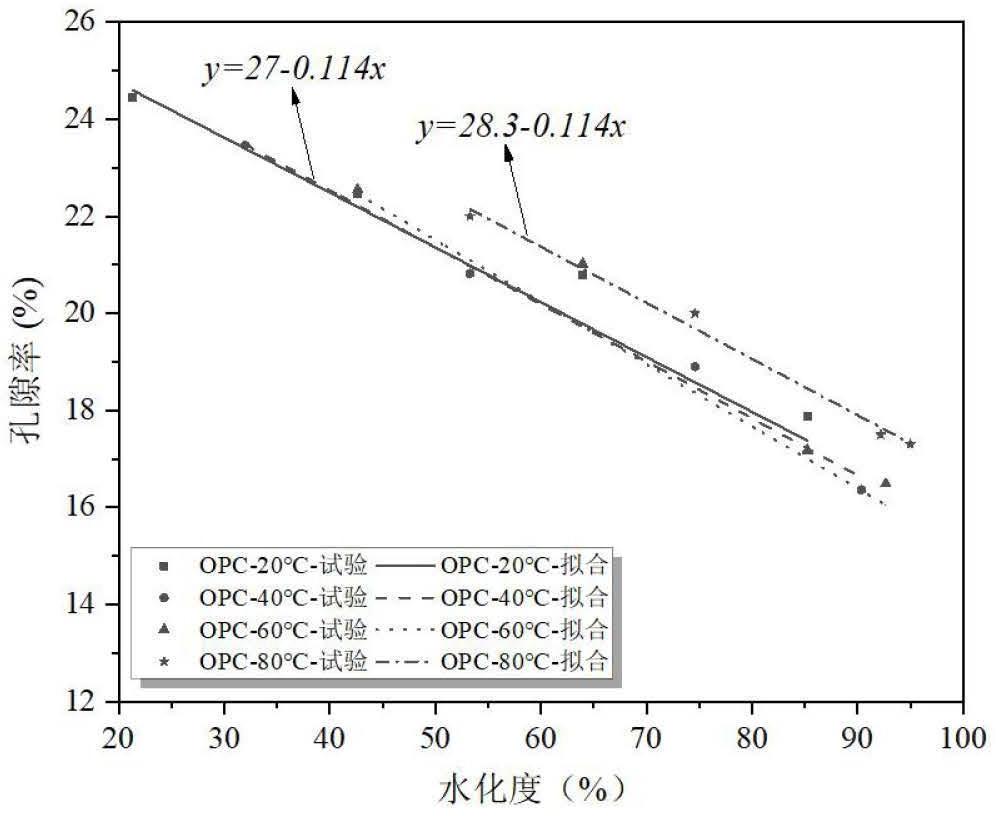
24、式中，e为存在温度损伤时混凝土的弹性模量；e0为无温度损伤时混凝土的弹模；ft为存在温度损伤时混凝土的抗拉强度；ft0为无温度损伤时混凝土的抗拉强度；ζ为与温度相关的损伤因子；φ为存在温度损伤时混凝土的孔隙率。混凝土的孔隙率由低场核磁测试得到。

25、当η(t,t,x,y,z)>1.0时混凝土一定会开裂；当0.7<η(t,t,x,y,z)≤1.0时混凝土存在开裂的可能性；当η(t,t,x,y,z)≤0.7时混凝土基本不会开裂。

26、有益效果

27、本发明公开了一种基于成熟度理论的大体积混凝土早期开裂指数及其时空分布预测方法，与现有方法相比，本发明提出的方法提供了一种准确预测任一温度历史、任一龄期的混凝土性能和变形的方法，提高了大体积混凝土开裂指数及其时空分布预测准确率且节省大量时间和人工成本。更重要的是可以假设系列混凝土配合比、假设多种施工养护边界条件、假设可能调控的不同拌合物入模温度，预测实际大体积混凝土的温度场、应变场、应力场、拉伸强度场和开裂指数及其时空分布，从而反向设计防裂混凝土配方、施工养护方法以及入模温度控制。