网络游戏区块链路地图时空高效路径搜索方法与流程

本技术涉及一种网络游戏地图路径搜索方法，特别涉及一种网络游戏区块链路地图时空高效路径搜索方法，属于网游地图搜索。

背景技术：

1、当前网络游戏特别是手游高速发展，如果仅依靠重复单一的打怪升级模式和单调而又简陋的图像画质，已经无法吸引玩家的注意。唯有提高游戏的可玩性以及服务器运转性能才能提高玩家黏性。对于一款游戏而言，人工智能控制系统在游戏中起着的作用日益凸显。而对于游戏中的人工智能控制系统来说，游戏场景中的路径搜索系统又是最基本的系统之一。由于游戏中的地图从一开始最早的封闭式地图再到无缝开放式的地图发展，游戏地图越做越大，导致标准的寻路算法很难满足一款高质量游戏的运转需求。

2、现有技术大多数游戏路径搜索系统，很难做到高效与准确这两个性能并存。在一个动态的大型地图中，问题表现为游戏人物在行走过程中极大地偏离目标位置或游戏人物在去往目的地的过程中，游戏人物因算法运算性能较差而产生的走走停停。更严重的是，明显可达目的地而寻路搜索系统判定寻路失败情形。在同样都确定能得出准确路线的搜索路径系统，能否满足可靠性、高效性、可行性、逼真性，是判定搜索路径系统好坏的标准。

3、游戏搜索路径算法所遇到难题，以及搜索路径算法在最终路径优劣上的衡量标准，都在指引着一款高质量游戏的发展方向。一种高效而又准确的搜索路径系统能给玩家带来真实且流畅的游戏体验，对于实际游戏算法的优化起着积极作用。

4、在地图类游戏的开发中,路径搜索算法是最根本和最重要的部分，找到一条正确无误的路径也是游戏人物的一项必备技能。当游戏地图逐渐趋于动态化、大型化发展，导致服务器中的运算量的急剧增多，还得顾及到游戏玩家在游戏真实感方面的需求，路径搜索算法的优化问题也成为游戏开发过程中的核心问题和提高游戏性能的瓶颈问题。

5、盲目式搜索路径算法不考虑问题本身特征的无信息式搜索算法，由于不考虑结点信息的蛮力搜索式算法，所以在时间和空间的两方面效率都极其低下，一般只能用于处理简单问题。当游戏的地图逐渐变得愈加复杂时，游戏地图中的结点愈发增多，而盲目式搜索算法处理起来力不从心。启发式搜索算法给解决复杂地图提供了一个新思路。

6、但启发式搜索算法在解决大型游戏地图的寻路问题时，其性能依然难以令人满意。其中的启发式区块搜索寻路算法，首先将大地图均匀的切分成若干个小地图，再通过将抽象结点设置在小地图的方式上，连接多个抽象结点进而形成多个抽象联通图，最后再在抽象联通图上进行启发式搜索算法来找出最佳路径。但由于启发式区块搜索算法在预处理和在线寻路阶段，均未将地图的障碍结点信息考虑在内，而只是进行简单而又生硬的划分。虽然能在一定程度上减少判断的时间，但容易造成不必要的时空浪费，阻碍了寻路搜索效率的进一步提高。

7、除上述问题和缺陷外，本技术需要解决的问题和关键技术难点还包括：

8、(1)标准的启发式搜索算法的open表所使用的逻辑结构不能高效的查找键值最小的结点，使用启发式搜索算法进行路径检索时，需要针对open表进行频繁的插入结点、查询结点以及删除结点操作，均会涉及到对表内信息反复读取和排序。如果open表的逻辑结构不当，则这些操作容易耗费大量的时间和空间。由于需要对open表中所有结点的键值信息进行比较之后,才能得出表中的估算值最小结点。所以，是否能选到合适的排序算法尤为关键。选择的目标旨在找到能减少对于open表的查询次数之余还能提高每次查询最小键值结点的效率，从而使得路径规划算法能够达到地图游戏中对于实时性的要求，进而提高玩家的满意度以及用户黏性。

9、(2)按值查询open表效率低下，如果想确定下一个遍历的结点，则需要将当前结点的八个方向上的结点都逐个进行判断，再决定对这些结点的进一步操作。其中，如果该结点并非为障碍结点，则需要根据open表中进行查询是否该结点已然存在，再来决定下一步的操作步骤。即在扩展下一结点这一步骤时，需要不断反复地在open表中进行按值查询结点的操作。而标准的启发式搜索算法中，open表的逻辑结构采用的是队列。无论是选择链表队列还是数组队列这两种存储方式中的任意一种，其按值查询的效率都为o(n)，查询效率不高。即便是将open表的逻辑结构由队列变为更能方便查询最小键值的最小二叉堆后，按值查询的效率也仅是由o(n)提升为o(logn)，依然存在提升空间。把open表进行按值查询操作的时间复杂度降至o(1)是本技术的目标之一。

10、(3)启发函数不能很好的满足高强度的寻路需求，启发函数能决定通过启发式搜索算法选取路径的成功与否，如果选择了恰当的启发函数，不仅能使游戏中的人物正确的朝着目标前行，还能使搜索路径过程顺畅而毫无阻碍即计算时间短而不出现卡顿。如果没找到合适的启发函数，则容易导致最终的搜寻结果并非最优路径,且在搜寻过程中效率极低，甚至搜寻出的路径与最优路径相去甚远。启发函数在计算上的难易程度由游戏地图中的启发信息总量决定，当启发函数复杂，则容易导致其所需的启发信息增多，增加计算量。但复杂的启发函数对结点信息筛选的条件更加严苛，排除的无效结点也自然更多，进而也能加快搜寻路径的效率。所以，如何平衡搜索精确度与搜索速度之间的矛盾，是游戏开发中躲不开的难题。在标准启发式搜索算法中，使用的是基于欧几里得距离的启发函数。算法虽然在执行上简单，并且从长度来看是最短的。但在游戏场景当中，游戏角色的行走往往不能按照直线路径。所以，通过欧几里得距离来计算起始结点到目的结点之间的距离与游戏人物的实际行走容易差别较大，实用性不强。相对于欧几里得距离函数，采用曼哈顿距离函数作为启发函数更具有实用价值。但曼哈顿距离在计算两点之间的距离时，只是简单的将其横坐标与纵坐标的绝对值之和相加。在真实的游戏地图中，游戏角色是可以朝着当前结点的八个方向前进的。在曼哈顿距离中,如果游戏角色要到达斜对角的结点时,只能先进行水平方向上的移动，再进行竖直方向上的移动。这样的移动方式不仅规划路线效率不高，而且过于生硬的行走方式就游戏的真实度而言，效果也不好，不能给玩家带来较为真实的游戏体验。

11、(4)当游戏地图规模较大时，现有技术在寻路过程中均没能将地图中的结点信息考虑在内。并且当障碍物疏密程度不一样时，即使是同一个算法的寻路性能也差异较大，难以达到实时性水平。标准启发式搜索算法与盲目搜索算法中的迪杰斯特拉算法的时间复杂度都较高，在处理大型地图的寻路问题时的效率难以令人满意，一味地将地图均匀地四分切割，并没有将地图中的障碍结点信息考虑在内，使得该算法在处理大面积非障碍结点地图之时，搜索路径的效率极为低下；在分区时只把起始结点与目标结点考虑在内，容易导致其它分区的寻路速度慢，而且过多的扩展结点也会造成时间上的浪费。在线寻路阶段均采用标准的启发式搜索算法，整个寻路算法的局限性表现在两个方面，一是在真是游戏场景中，障碍结点所占比例并不高，即大部分分区是空白区域，而在空白区域上使用启发式搜索算法实则效率低下且完全没有必要；二是标准的启发式搜索算法本身就有存在有待提升的方面。搜索路径系统无法满足可靠性、高效性、可行性、逼真性的需求。

技术实现思路

1、本技术基于启发式区块搜索算法在预处理、在线寻路以及所使用的启发式搜索算法三个方面分别进行优化，提出了使用向量迭代余弦函数作为启发式搜索算法的启发函数、使用索引数组和采用最小二叉堆存储open表结构。该启发函数在寻路过程中，将结点的方向信息考虑在内，能有效地剔除大量无用结点。基于最小二叉堆迭代逻辑结构能快速地读取最小值，且方便插入删除。使用索引数组能以o(1)的时间复杂度查询到结点是否存在于open表内。并在启发式区块搜索算法寻路过程中，使用优化后的启发式搜索算法。在启发式区块搜索算法在执行过程中，提出了根据区域间障碍结点的分布情形来标注该区域的状态，并由该状态信息决定当前区域是否继续进一步的划分以及得到抽象路径之后，在当前子区域上路径细化的方式。如果当前子区域状态信息为非障碍结点，区域不继续划分并且在在线寻路阶段使用采用bresenham直线算法而非启发式搜索算法来进行路径细化，搜索路径系统可靠性、高效性、可行性、逼真性都有较大程度的提高。

2、为实现以上技术效果，本技术所采用的技术方案如下：

3、网络游戏区块链路地图时空高效路径搜索方法，基于启发式区块搜索算法在预处理、在线寻路以及所使用的启发式搜索算法三个方面分别进行优化，包括基于向量迭代余弦的启发式优化搜索算法、基于地图信息链路启发式区块搜索优化算法；

4、基于向量迭代余弦的启发式优化搜索算法包括优化open表逻辑结构、基于索引数组优化按值查询open表、基于向量迭代余弦距离的启发函数，在寻路过程中减少访问结点的总数，在open表的存储结构上采用方便查询最小键值以及插入删除都效率极高的最小二叉堆的方式和使用索引数组对启发式搜索算法进行优化；

5、基于地图信息链路启发式区块搜索优化算法分别从所需系数设置、子区域的划分、子区域的抽象化、在线寻路四个方面优化，寻路过程包括预处理阶段以及在线寻路两部分，预处理包括地图选取、划分子区域和形成抽象连通图三个步骤；在线寻路阶段包括插入起始结点与目标结点、在抽象结点上产生最短路径、抽象路径的细化三个步骤；将地图中障碍点的信息考虑在内对启发式区块搜索算法进行优化，首先，在对地图进行划分时根据当前子区域的状态信息来决定是否进行下一步划分，并且在形成抽象连通图后，采用优化后的启发式搜索算法得到一条抽象路径，然后，再根据子区域状态信息的不同来决定采用基于余弦向量优化的启发式搜索算法或是直角线距离来对抽象路径进行细化，最终得到完整的路径。

6、优选地，优化open表逻辑结构：基于启发式搜索算法需要反复从open表中选取最键值小值并将其删除的这一特征，采用最小二叉堆迭代逻辑结构来处理open表中的结点信息，父结点的键值总是不小于其左右孩子的键值，并且每一个结点的子树又都满足于最小二叉堆的条件，如此递归定义满足搜寻open表并寻得最小启发函数值的需求，采用最小二叉堆迭代逻辑结构来处理open表中各个数据之间的关系，高效获取表中的键值最小值和删除表中键值最小的结点；包括添加新链路结点和删除键值最小的结点。

7、优选地，基于向量迭代余弦距离的启发函数：

8、在判断下一个结点信息时，将该结点与目标结点连线所在的方向考虑在内，将背离目标结点方向上的结点排除在外,避免规划路径因为添加一个远离了目标结点的结点后，使得路径发生折返、倒退，在考虑结点方向时，使用向量迭代余弦函数作为偏移量，添加到标准启发式搜索算法的启发函数之中，保障路径规划算法在扩展下一结点时，让路径朝着目标结点的方向前进；

9、采用在原有基于欧几里得距离基础上添加负值的向量迭代余弦距离作为偏移量，作为对原有启发函数的优化，通过将结点方向信息考虑在内的方式，避免算法所规划的路径出现折返，如式2、式3所示：

10、h’(n)＝h0(n)+hcos(n)     式2

11、hcos(n)＝-ωcosβ     式3

12、式中，h’表示为优化后的启发函数，其值于标准基与欧几里得距离的启发函数h0再加上向量迭代余弦函数值，ω为可调整的权重，β为该结点和起始结点连线后和最优路径的角度之差，其中，这里的最优路径指的是从起始结点到目标结点所连接的一条直线；

13、如果起始结点为s点，目标结点为n，其中结点a和结点b是算法在扩展中所需考察的结点。向量与向量的夹角是α，向量与向量的夹角是β，如果使用标准的启发式搜索算法时，a、b两个结点的f值相等，则这两个结点均要进行比较。而采用向量迭代余弦作为启发函数的偏移量后，如果结点b路径代价值g与结点a的相同，而由于结点b的所在方向已经偏离了最优路径，即β大于α，结点b的估算函数值f自然比结点a的值要大，则结点b就会被视为无用结点。

14、在标准启发式搜索算法中，a、b两个结点的f值相等，如式4所示：

15、f(a)＝g(a)+h(a)

16、f(b)＝g(b)+h(b)

17、fcos(a)＝fcos(b)   式4

18、添加负号的余弦函数单调递增，得出以下结论：

19、hcos(a)＝-ωcosα

20、hcos(b)＝-ωcosβ

21、hcos(a)＜hcos(b)    式5

22、再把上述结果代入到优化后的启发函数中，即结合式4、式5和式2后，得到：

23、h’(a)＝g(a)+h(a)+hcos(a)

24、h’(b)＝g(b)+h(b)+hcos(b)

25、h’(a)＜h’(b)    式6

26、a点相较于b点更接近从起始结点到目标结点之间的最优路径上，a点的启发函数值则小于b点的值，如果点a除了与最优路径上形成的夹角比b点更小之外一切数据与点b相同，则点a会被选为下一个遍历结点，而且通过该筛选结点的方式，能使得选择的下一个结点都更加趋近于最优路径，减少无用结点考察数量。

27、优选地，基于地图分布信息优化启发式区块搜索算法，在对大规模地图进行分区时将地图的结点信息考虑在内，并且当处于在线寻路的过程中,对使用启发式搜索算法或bresenham直线算法的情形进行分类处理；

28、将地图中的结点信息考虑在内，并根据障碍结点的分布信息对游戏地图进行不均匀划分子区域，且在划分时，使用一个状态位来表明该子区域的障碍物分布信息λ，依照该状态位对子区域的下一步操作进行判断，障碍物信息状态λ分以下3种情形：一是子区域均为空白即当前区域中均为非障碍物结点，则令λ＝0；二是子区域的障碍物结点大于设定的临界值，即λ＝1；三是子区域的障碍物结点比例小于设定临界值,则继续进行四划分,直至划分次数≤4为止，接着在划分后的子区域上，选取关键点连接使之形成抽象联通图，再在抽象连通图上使用基于余弦向量优化的启发式搜索算法，得到一条抽象路径，最后，根据该子区域λ的状态信息分情形细化抽象路径，如果λ＝0时，则使用bresenham直线算法；否则采用优化后的启发式搜索算法得到实际路径，在搜索路径过程中将引入三个系数，分别为：表明子区域的状态信息λ、事前设定的障碍结点临界值β、子区域障碍结点所占比δ。

29、优选地，所需系数设置：子区域障碍结点所占比δ是该子区域内障碍物结点所占总结点的比例，定义如式7：

30、

31、表明子区域状态信息的λ是每个小分区的状态标示器，且λ取值如果非0，则必为1，当入为0时表明，当前子区域的结点均为空白结点即非障碍结点，则不再对该区域进行切割，并且处于在线寻路的阶段中，对λ值为0的子区域采用bresenham直线算法；

32、临界值β的取值在0到1之间，当β值越大时，所选取的关键点越多，代表对该地图划分越精细。

33、优选地，子区域的划分：首先将地图平均分成四等分，终止条件中考虑具体当前子区域上的结点信息，终止条件与临界值β和障碍结点占比δ相关，且根据这二参数的相对大小分三种情形：

34、1)δ＝0：表示当前子区域不存在障碍结点，则不再继续对当前子区域进行下一步划分，直接采用bresenham直线算法来规划路径，并且把当前子区域的状态信息值λ设为0；

35、2)δ＞β：即当前子区域的障碍结点占有率大于事前设定的临界值，表明该子区域的障碍结点较多，且划分区域的精细程度已满足要求，无进一步划分的必要，采用基于向量迭代余弦的启发式搜索算法获取路线，并把当前子区域的状态信息设置为1；

36、3)δ＜β：即当前分区的障碍结点较少，继续对当前子区域进行四分，再进行判断，如果四分的次数已到达四次，则终止分层，并把当前子区域的状态信息设置为1。

37、优选地，子区域的抽象化：分为对地图划分、形成抽象图以及在线寻路三个步骤，抽象结点位于相邻子区域的连通口上，在算法开始前设置一个临界值，当连续的连通结点个数小于这一临界值时，则选择中间的连通结点作为关键点；而当连续的结点个数大于这一临界值时,选择两边的结点作为关键点；先将同一子区域内的关键结点相连，再将相邻子区域的关键点相连，则形成最终的抽象连通图，完成预处理。

38、优选地，在线寻路：

39、1)插入起始与目标结点

40、形成带有关键结点的抽象联通图，在联通图中插入起始结点与目标结点时，有两种情形，一是起始结点和目标结点本身就与抽象出的关键结点相重合，则不再进行插入起始结点和目标结点的步骤，而是直接进行寻路；二是起始结点与目标结点并未与抽象结点重合，将起始和目标结点与其所在的区域上的抽象结点进行连接，完成插入步骤；

41、2)获取抽象路径

42、(1)λ值为0时，当前子区域为空白区域，结点均为非障碍结点，在非障碍结点区域上直接使用bresenham直线算法进行寻路即可；

43、(2)λ值为1时，当前子区域障碍结点的占有率大于设定临界值，当前区域内障碍结点数较多，则在该区域内使用经由启发式搜索算法进行路径搜索，到抽象路径各个结点之间的路径均完成细化后，在最底层的区域内得到一条实际路径。

44、优选地，寻路过程预处理：

45、(1)地图选取：首先对游戏地图进行量化，将其抽象化为二维网格图再进行后续处理，将待处理的游戏地图设为正方形，且面积为4的整数次幂；

46、(2)划分子区域：依照当前子区域的障碍结点的占有率对该区域进行状态信息的标注，再根据不同子区域的分区状态信息与事前设定的障碍结点占有率临界值之间的大小关系，来判断是否要进行下一步的区域再划分；

47、(3)形成抽象连通图：当连续的连通结点个数小于2时，则选择中间的连通结点作为关键点；当连续的结点个数大于这一临界值时，选择两边的结点作为关键点；首先，先将同一子区域内的关键结点相连，再将相邻子区域的关键点相连，形成最终的抽象连通图。

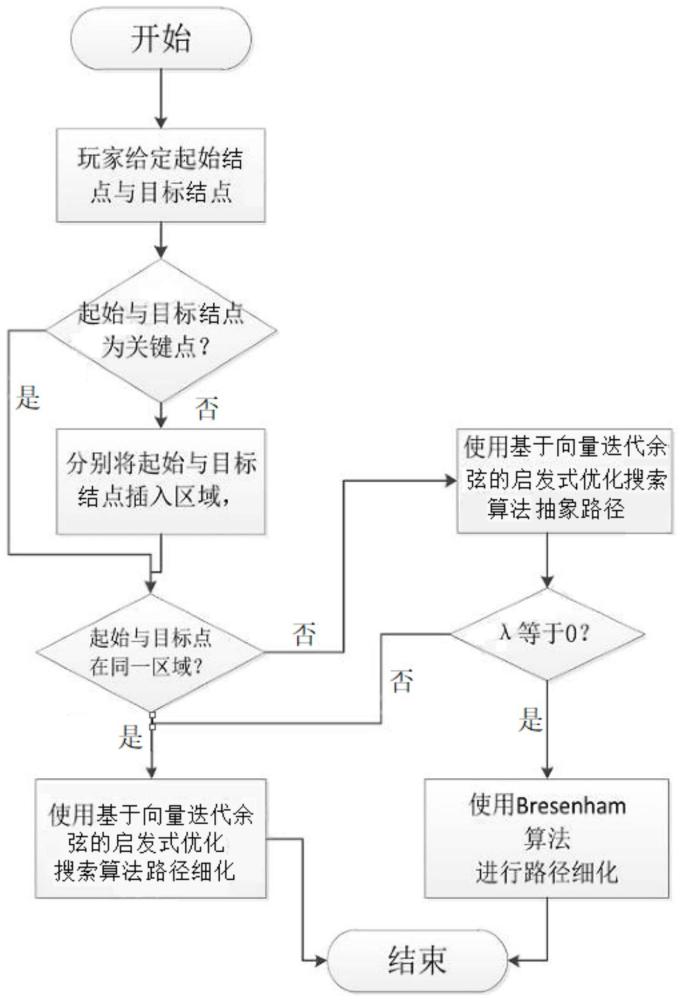
48、优选地，在线寻路：

49、步骤一，插入起始结点与目标结点：先判断起始结点和目标结点是否已经被抽象成关键结点，如果是，则跳过此步骤，进行步骤二，如果目标结点和起始结点暂未与关键点重合，则将这两特殊结点与其子区域边界上的关键结点相连接。

50、步骤二，得到抽象的最短路径：判断目标结点与起始结点是否处于同一个子区域，如果是，则跳过此步骤，进行下一步骤，如果不在同一子区域，则在起始结点、目标结点以及关键结点之间使用优化后的启发式搜索算法，得到一条抽象路径；

51、步骤三，路径细化：如果状态信息1为0，则在细化路径时，采用bresenham直线算法来规划路径，在每次画点时，选取与直线的交点y坐标的差最小的那个点；否则便使用优化后的启发式搜索算法来规划实际路径。

52、与现有技术相比，本技术的创新点和优势在于：

53、(1)本技术基于启发式区块搜索算法在预处理、在线寻路以及所使用的启发式搜索算法三个方面分别进行优化，提出了使用向量迭代余弦函数作为启发式搜索算法的启发函数、使用索引数组和采用最小二叉堆存储open表结构。该启发函数在寻路过程中，将结点的方向信息考虑在内，能有效地剔除大量无用结点。基于最小二叉堆迭代逻辑结构能快速地读取最小值，且方便插入删除。使用索引数组能以o(1)的时间复杂度查询到结点是否存在于open表内。并在启发式区块搜索算法寻路过程中，使用优化后的启发式搜索算法。在启发式区块搜索算法在执行过程中，提出了根据区域间障碍结点的分布情形来标注该区域的状态，并由该状态信息决定当前区域是否继续进一步的划分以及得到抽象路径之后，在当前子区域上路径细化的方式。如果当前子区域状态信息为非障碍结点，区域不继续划分并且在在线寻路阶段使用采用bresenham直线算法而非启发式搜索算法来进行路径细化，此种分类方式，大幅提高寻路效率和准确度。

54、(2)本技术创造性的提出了基于向量迭代余弦的启发式优化搜索算法，一是在启发函数的设计上，采用最符合实际情形的向量迭代余弦距离来作为基于余弦向量优化的启发式搜索算法的启发函数。二是在发现启发式搜索算法在寻路过程中需要反复查看open表并且删除open表中最小键值的这一特征时，对标准启发式搜索算法中open表的存储结构采用最小二叉堆的结构来进行优化，最小二叉堆能够以o(1)的时间复杂度获取当前最小键值，并且在插入删除结点都有极优的性能，恰好满足open表的操作需求。三是在扩展下一结点时，需要反复判断该结点是否已经存在于open表内。如果依旧采用最小二叉堆迭代逻辑结构，则按值查找open表效率不高。本技术引入一个二维的索引数组，用数组的下标对应地图中的位置，数组中存放的值来表示该结点是否存在于open表中，效率明显提高。

55、(3)本技术创造性的提出了基于地图信息链路启发式区块搜索优化算法，分别从所需系数设置、子区域的划分、子区域的抽象化、在线寻路四个方面优化，寻路过程包括预处理阶段以及在线寻路两部分，预处理包括地图选取、划分子区域和形成抽象连通图三个步骤；在线寻路阶段包括插入起始结点与目标结点、在抽象结点上产生最短路径、抽象路径的细化三个步骤；在对大规模地图进行分区时将地图的结点信息考虑在内，并且当处于在线寻路的过程中,对使用启发式搜索算法或bresenham直线算法的情形进行分类处理，除此之外，在要使用启发式搜索算法的部分，将启发式搜索算法进一步优化，进一步提升算法的寻路效率。搜索路径系统可靠性、高效性、可行性、逼真性都有较大程度的提高。