状态受限的CSTR自适应神经网络控制方法及系统与流程

本发明涉及cstr控制，特别是指一种状态受限的cstr自适应神经网络控制方法及系统。

背景技术：

1、由于连续搅拌反应釜（continuously stirred tank reactor，cstr）内部化学反应放热过程的复杂性和非线性，导致系统模型存在严重的非线性与时变性，使得控制变得复杂。此外，釜内反应过程受到外部干扰的影响较敏感，增加了控制的难度。cstr中的化学反应过程由于反应条件、原料特性的复杂性，存在多个相互影响的变量，这将导致控制方向未知。同时，由于原料组成的变化、设备性能的波动或外部环境的干扰等因素，造成系统的参数（如温度、压力、流量等）在操作过程中发生动态变化，也将引起控制方向未知。现有的技术没有充分考虑上述非线性、时变性、外界未知干扰、控制方向未知、系统存在未建模动态等情况对系统的不利影响，导致控制效果一般，将会影响化学反应的速率、转化率和产物质量。

技术实现思路

1、为了避免上述因素对控制系统产生不利影响，本发明提出一种状态受限的cstr自适应神经网络控制方法及系统，建立了cstr模型，同时基于神经网络方法、障碍李雅普诺夫函数、nussbaum补偿技术提出了自适应神经网络状态受限控制器，确保系统对指令信号进行快速精确的跟踪。

2、本发明的技术方案是这样实现的：状态受限的cstr自适应神经网络控制方法，包括以下步骤：

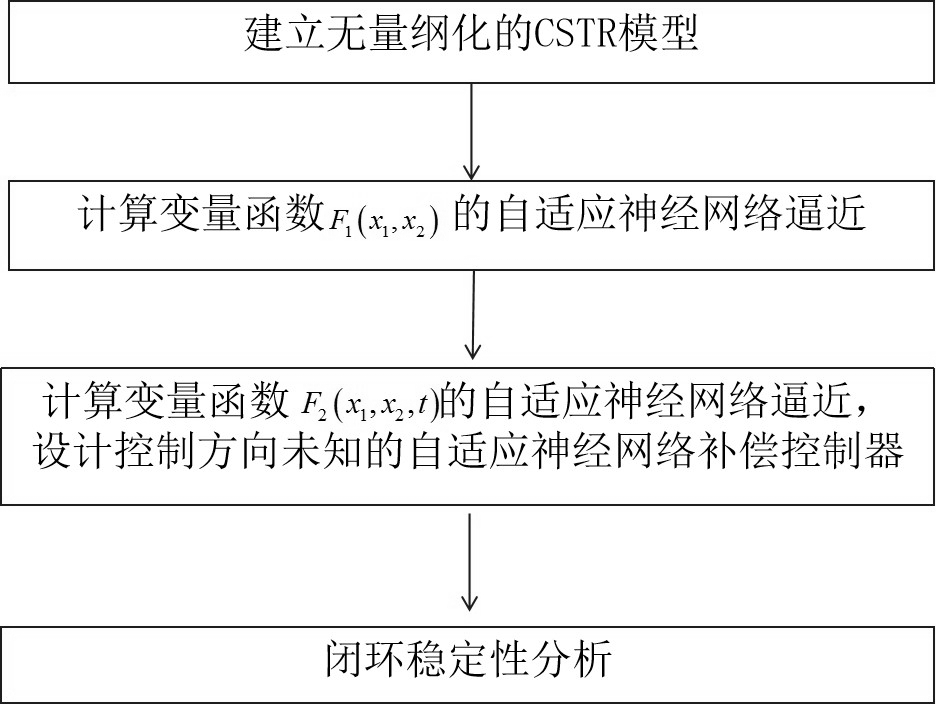
3、步骤1、建立无量纲化的cstr模型；

4、无量纲化的cstr模型方程如下：

5、             (1)

6、其中，为符号可变的未知有界时变函数，未知函数为模型无量纲温度干扰与未建模动态，未知函数和为建模过程中的未知非线性动态；与为非线性函数；变量为无量纲化浓度，；变量为无量纲化温度，；变量为无量纲化控制输入，，，为执行器输出的最大控制幅值；

7、步骤2、定义为跟踪误差，为时变理想信号；

8、定义如下对称barrier lyapunov函数

9、                            (3)

10、其中为自然对数，设计参数为常数；

11、定义辅助控制变量、满足，定义变量函数为

12、                      (4)

13、基于神经网络逼近方法，计算变量函数的自适应神经网络逼近；

14、步骤3、定义变量函数为

15、    (14)

16、基于神经网络逼近方法，计算变量函数的自适应神经网络逼近；

17、基于nussbaum补偿技术以及障碍李雅普诺夫函数，设计控制方向未知的自适应神经网络补偿控制器。

18、进一步地，步骤1中，非线性函数与具体定义如下：

19、         (2)

20、常量为达姆寇勒数，；常量为无量纲化活化能，；正常数为无量纲化传热系数，；常量为绝热温升系数，；常量为出口体积流速，变量为反应物浓度，变量为进口浓度，常量为指数因子，常量为活化能，常量为摩尔气体常数，变量为进口温度，变量为釜内的绝对温度，常量为连续搅拌反应釜体积，常量为反应热，变量为出口密度，常量为出口热容，变量为时间，常量为冷却剂温度，常量为传热系数，其中，变量、变量、变量、变量均为随时间t变化的变量。

21、进一步地，步骤2，计算变量函数的自适应神经网络逼近的方法如下：

22、2.1、对式(3)求导可得

23、   (5)

24、将的神经网络逼近形式定义为，为函数输入向量，利用神经网络方法对变量函数进行如下逼近：

25、                    (6)

26、其中，为神经网络的理想权值向量，正整数表示该神经网络中所包含的神经元节点数量；为已知高斯径向基函数向量，，定义为

27、                     (7)

28、其中，感受域中心为向量，感受域宽度为常量；为神经网络逼近误差，通过增加神经网络的神经元节点数量使其减小；

29、2.2、定义第二个李雅普诺夫函数

30、                 (8)

31、其中，为理想权值向量的自适应估计值，为理想权值向量的估计误差；，为常数，；

32、设计辅助控制变量为：

33、                 (9)

34、其中，设计参数为常数；

35、由式(5)、(6)、(8)和(9)可得

36、 (10)

37、设计自适应估计值的自适应律为

38、                     (11)

39、其中，设计参数为常数

40、由式(6)和(11)，得到变量函数的自适应神经网络逼近为

41、                    (12)

42、由式(11)计算神经网络的理想权值向量的自适应估计值，进而利用式(12)计算变量函数的自适应神经网络逼近。

43、进一步地，步骤3中，计算变量函数的自适应神经网络逼近的方法如下：

44、3.1、定义第三个李雅普诺夫函数

45、                 (13)

46、定义变量函数为

47、              (14)

48、由，以及式(13)、(14)、(1)和(2)可知

49、(15)

50、将变量函数的神经网络逼近形式定义为，为函数输入向量；

51、利用神经网络方法对变量函数进行如下逼近：

52、                    (16)

53、式(16)中为神经网络的理想权值向量，正整数表示该神经网络中所包含的神经元节点数量；为已知高斯径向基函数向量，，定义为

54、                     (17)

55、其中感受域中心为为向量，感受域宽度为为常量；为神经网络逼近误差，通过增加神经网络的神经元节点数量使其减小；

56、3.2、定义第四个李雅普诺夫函数

57、              (18)

58、其中，为理想权值向量的自适应估计值，为理想权值向量的估计误差；，为常数，；

59、设计辅助控制信号为：

60、              (19)

61、其中，设计参数为常数；

62、设计自适应估计值的自适应律为

63、                     (20)

64、其中，设计参数为常数；

65、由式(16)和(20)，得到变量函数的自适应神经网络逼近为

66、             (21)

67、由式(20)计算神经网络的理想权值向量的自适应估计值，进而利用式(21)计算变量函数的自适应神经网络逼近。

68、进一步地，步骤3中，计算设计控制方向未知的自适应神经网络补偿控制器的方法如下：

69、对于任意变量或常量，定义其nussbaum函数，满足：，；

70、设计无量纲化控制输入为

71、                          (22)

72、其中，变量和为辅助控制信号；

73、设计辅助控制信号为

74、                     (23)

75、其中，设计参数为常数；

76、利用式(19)、(23)计算辅助控制信号，进而利用式(22)计算无量纲化控制输入，无量纲化控制输入即为控制方向未知的自适应神经网络补偿控制器。

77、进一步地，还包括步骤4闭环稳定性分析

78、由式(15)、(16)、(18)、(19)、(22)和(23)得

79、(24)

80、定义常数为

81、              (25)

82、基于，根据杨氏不等式，由式(10)、(11)、(20)、(24)和(25)可知

83、       (26)

84、其中，为常数；

85、对式(26)的等号两侧同乘，并在区间积分可得：

86、     (27)

87、全局有界，则存在常数，满足

88、(28)

89、因此全局有界，结合式(27)可知

90、                       (29)

91、由于，结合式(18)可知，

92、因此结合式(29)可知

93、         (30)

94、通过增大控制参数、使误差任意小。

95、一种状态受限的cstr自适应神经网络控制系统，包括存储器、处理器及存储在存储器上并可在处理器上运行的计算机程序，其特征在于，所述处理器执行所述计算机程序时实现如所述的控制方法。

96、本发明的有益效果：

97、本发明基于神经网络方法、障碍李雅普诺夫函数、nussbaum补偿技术提出了自适应神经网络状态受限控制器，所设计的控制器能够确保系统外部存在未知干扰、内部存在未知非线性、控制方向未知时对指令信号进行快速精确的跟踪，同时可以使跟踪误差始终被限制在预设的边界内，具有更高的控制性能，应用范围更广。