基于压路机振动轮的加速度及其与压实度间关联测试方法与流程

本发明涉及沥青混合料压实测试，具体而言，涉及一种基于压路机振动轮的加速度及其与压实度间关联测试方法。

背景技术：

1、当前，沥青混合料在摊铺后相对较为疏松，其结构强度与弹性刚度较小，而阻尼相对较大，初压时因大部分振动能量被吸收，仅有较少的振动能量反馈；而随着碾压遍数的增多，骨料间隙减小，沥青混合料逐渐密实，刚度不断增大，阻尼逐渐减小，其振动轮的振动反馈也逐步增大；当沥青混合料达到一定的密实程度后，振动压路机偏心装置的不对称性将使其出现跳振现象，其获得的振动加速度信号会同步出现过增大情况，也就可能致使路面出现过碾压状态，进而导致大石料容易被压碎，严重影响后续路面的承载能力与使用寿命。

技术实现思路

1、为此，本发明提供了一种基于压路机振动轮的加速度及其与压实度间关联测试方法，以解决现有技术中在针对路面沥青混合料进行压铺筑实时，沥青混合料随其密实作用反馈的振动加速度信号会出现过增大，致使路面出现过碾压状态，进而导致大石料易被压碎，影响后续路面的承载能力及使用寿命的问题。

2、为了实现上述目的，本发明提供如下技术方案：

3、一种基于压路机振动轮的加速度及其与压实度间关联测试方法，具体包括如下步骤：

4、基于压路机振动轮的作业特征适配性选取测振加速度传感器；

5、基于选取的测振加速度传感器配合振动轮进行振动加速度信号现场路面实测采集；

6、将现场路面实测采集的振动加速度信号进行信号调理；

7、对于经信号调理之后的振动加速度信号进行离散性检验与数据分析；

8、计算分析路面压实度与振动加速度有效值之间的实测关系。

9、在上述技术方案的基础上，对本发明做如下进一步说明：

10、作为本发明的进一步方案，所述基于压路机振动轮的作业特征适配性选取测振加速度传感器，具体包括：

11、基于压路机振动轮的作业特征适配性选择测振加速度传感器，以测得并通过振动轮的振动加速度间接反映被压实材料的压实度；

12、具体地，基于如下原则依照振动轮的作业特征选取测振加速度传感器：

13、由于振动过程中，振动轮的位移和振动速度均相对较小，前者通常不超过2毫米；但相应激振力和振动加速度一般较大，振动加速度一般在0～15g范围变动，因此，选择量程超过0～15g范围，且信噪比相对较高的传感器；

14、由于测振加速度传感器自身对振动特征存在影响，因此在测振时，为了减小影响使检测结果更为精确，选择传感器的质量和体积均小于特定规格；

15、振动压路机的工作频率较高，为满足高频工况的检测需求，其对于测振加速度传感器的使用频率范围要求较宽，因此选择的测振加速度传感器的谐振频率大于压路机的工作频率，避免共振的发生影响检测结果，保护检测器件；

16、结合上述要求，最终选择的测振加速度传感器的参数为：最大振动加速度为20g，分辨率为0.01g，精度为0.5％，更新速率为100hz；由于压路机压实作业过程中，振动轮的位移和振动速度相对较小，但激振力和振动加速度一般比较大，因此所选测振加速度传感器可以很好地反映沥青混合料的压实特性。

17、作为本发明的进一步方案，所述基于选取的测振加速度传感器配合振动轮进行振动加速度信号现场路面实测采集，具体包括：

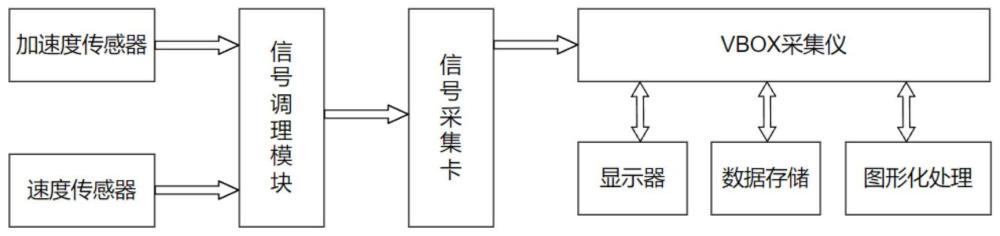
18、将所选的测振加速度传感器与相应的vbox采集仪器设备通过电路相连设置，之后进行现场调试确认；

19、通过胶水将测振加速度传感器粘附于振动压路机未经减振的振动马达一侧部，以确保振动加速度信号采集的准确性；

20、依照预定碾压工艺处理现场路面以作为试验段；

21、作为试验段的现场路面设置为沥青混合料路面中面层；

22、确定测振加速度传感器的采样频率，并进行测试系统相关参数设置，使振动压路机保持5km/h的速度匀速作业，并依照预定碾压工艺进行振动加速度信号采集，所述碾压工艺具体为：双钢轮压路机初压1遍、胶轮压路机揉搓2遍、双钢轮压路机高振幅低振频2遍、低振幅高振频2遍、最后进行收面处理；

23、在上述初压之后的每遍压实后均进行现场压实度采样，并收集采样样品。

24、作为本发明的进一步方案，所述将现场路面实测采集的振动加速度信号进行信号调理，具体包括：

25、由于测振加速度传感器输出的电信号较微弱，在将测得的振动加速度信号送入a/d转换模块之前，对振动加速度信号进行直流隔离与放大处理；而后为使测得的振动加速度信号中的干扰减少，对于振动加速度信号进行滤波处理；

26、将振动加速度信号进行直流隔离；

27、测振加速度传感器输出的振动加速度信号中，除了所需的振动电信号之外，还包括测振加速度传感器的工作电流信号，该工作电流信号为混杂于振动加速度信号中的直流分量，为了使其不影响后续处理，对其进行分离过滤放大；

28、将振动加速度信号输入之后流经电容c，电容c将振动加速度信号中的直流分量去除后，一端经电阻r接地，另一端接放大器作为其正向输入；u1是电信号流经r后与地面形成回路的接地电动势，由运算放大器的工作原理可知，放大器正向输入端与反向输入端电动势相等，而电路输出端又与放大器反向输入端电动势相等，所以输出端电动势等于放大器输入端电动势即，u2＝u1；在流经电容c的电流一定时，通过调节电阻r的值来控制电路的输出；

29、由于电路中测振加速度传感器的工作电流是由一个稳压器提供，因此在输出振动加速度信号经电容后去除直流，再接放大器输出；振动加速度信号接电容后由以下公式得出信号的截止频率：

30、

31、将分离过滤放大的振动加速度信号进行低通滤波；

32、在将振动加速度信号中的直流分量去除后，进一步对振动加速度信号进行滤除高频噪声处理；

33、选择低通滤波器；

34、由于巴特沃斯滤波器的幅频响应曲线单调下降，且响应较平滑、失真小等优点，因此采用巴特沃斯低通滤波器实现振动加速度信号的低通滤波；

35、选取测试压路机为悍马120双钢轮压路机，双钢轮压路机的作业振动频率主要集中在30～60hz之间，以振动频率为42或50hz为例，将低通滤波器的通带截止频率根据振动加速度信号的特征取为ωp＝175hz，通带内最大衰减为αp≤1db，阻带的截止频率取为ωs＝400hz，其最小衰减为αs≥20db；

36、以上参数的设置目的是使高频噪声(400hz以上)在经过滤波器时迅速衰减无法顺利通过，而低频信号(175hz以内)则顺利通过；175～400hz的信号处于过渡带内，其衰减在1～20db之间，衰减程度由低频到高频逐渐增大；

37、结合上文的条件，根据衰减函数的定义可得如下表达式：

38、α(ω)＝-20lg|h(jω)|      (2)

39、-20lg|h(jωp)|≤1       (3)

40、-20lg|h(jωs)|≥20       (4)

41、对式(3)和(4)求解可得：

42、δp＝1-|h(jωp)|≤1-10-0.05≈0.109     (5)

43、δs＝|h(jωs)|≤10-1＝0.1         (6)

44、其中，|h(jω)|2、|k(jω)|2、|h(jω)|分别为巴特沃斯低通滤波器的模平方函数、逼近特征函数和模频特性，其表达式如下所示：

45、|k(jωs)|2＝k(jω)k(-jω)＝(jω/ωc)n(-jω/ωc)n＝(jω/ωc)2n    (7)

46、

47、

48、其中：n—滤波器的阶数，ωc—3db截止频率；

49、由式(9)可知，随着频率ω的增加，巴特沃斯低通滤波器的幅频特性单调下降，其下降速率随着阶数n的增加而增大，幅度下降越快表明其过渡带越窄，信号衰减越快，阻带内越接近零，巴特沃斯低通滤波器的幅频特性越接近理想的矩形幅频特性；当ω＝ωc时，由式(9)可得出

50、

51、已知：

52、

53、由以上两式解得：

54、

55、

56、

57、将上文数据带入计算可得：

58、n≥3.597，n＝4，ωc＝225hz；

59、四阶巴特沃斯低通滤波器的系统函数h(s)可由查表获得：

60、

61、将相应数据带入可得：

62、

63、为了降低硬件设计难度，将四阶的巴特沃斯低通滤波器分解为两个二阶的级联，其传递函数也相应由如下两个二阶项相乘表示：

64、

65、为使进一步计算简便，在设计的二阶巴特沃斯低通滤波器中使相关参数满足如下条件：

66、r1＝r2＝r

67、c1＝c2＝c                    (15)

68、ωc＝225hz

69、选取c＝1μf，可解得r≈700ω；

70、四阶巴特沃斯低通滤波器两个阻尼系数分别为：

71、ξ1＝0.7654

72、ξ2＝1.8477                (16)

73、两个零频增益分别为：

74、g01＝3-ξ1＝2.2346

75、g02＝3-ξ2＝1.1523                (17)

76、组成四阶巴特沃斯低通滤波器的两个二阶的巴特沃斯低通滤波器的两极增益如下两式所示：

77、

78、

79、选取r＝10kω，则r01＝12.346kω，r02＝1.523kω；

80、根据以上结果，完成振动加速度信号的低通滤波计算，由于测试压路机的振动频率为42或50hz，因此，为提高采集准确性，通过带通方式对测得的振动加速度信号进行滤波处理，即保留30～70hz范围内的信号，阻掉低于10hz和高于150hz信号，最终得到所需的振动轮实际振动加速度信号。

81、作为本发明的进一步方案，所述对于经信号调理之后的振动加速度信号进行离散性检验与数据分析，具体包括：

82、当前压路机作业时的振动频率为42或50hz，当以50hz频率振动时，其一个振动周期为0.02s，压路机的碾压作业速度为5km/h，则其一个振动周期前行2.8cm，计算第10～30个振动周期内加速度平均值的标准偏差；

83、经计算可知，随着周期个数的不断增加，其标准偏差越小，且在第20～22个周期内标准偏差为0.635，相对较低，数据的关联程度较好，同时结合后续现场压实度的取样，故，选取20个周期及其倍数的加速度平均值作为实测加速度有效值，亦即，压路机每行驶0.56m对应采集一个加速度有效值，据此计算得到沥青混合料中面层不同碾压遍数下的加速度有效值；

84、采用“偏度、峰度检验法”来进行有效数据分析；

85、依前文所述，20个周期为0.4s，选取40s的压实度检测数据，通过信号处理后获得100个连续的加速度有效值，具体如下：

86、假设h0，数据来自正态总体，n＝100，则有：

87、

88、

89、

90、则样本的中心矩为：

91、b2＝a2-a12；b3＝a3-3a2a1+2a13；b4＝a4-4a2a12-3a14；

92、其中：

93、则样本偏度g1和样本峰度g2分别为g1＝b3/b23/2＝-0.052，g2＝b4/b22＝2.716；

94、

95、显著性水平α代表当h0为真时，h0被拒绝的概率；设在标准正态分布上的α/4分位点用zα/4来表示，则当α取值0.05时，对应的zα/4＝2.249，此时若μ1≥zα/4、μ2≥zα/4则该样本总体不为正态分布，但由于μ1、μ2均小于2.249，因此判断h0成立，也就是说，通过本系统获得的一系列加速度数据集为正态分布，故当置信水平为0.95时，tα/2＝1.96，对应的置信区间为(71.47，73.07)；在此区域内的数据保留，其余剔除，由此获得的加速度有效数据；

96、经上述计算得到的沥青混合料中面层在不同碾压遍数下随时间变化的加速有效值，在同一压实遍数情况下，振动加速度有效值随时间变化基本在一条水平线处于特定阈值范围内上下浮动；此外，在双钢轮压路机初压第一遍以及采用低振频、高振幅振动的两遍压实时，随着压实遍数的增加路面压实度随之增加，同时相应时间点内的振动加速度有效值变大；而在双钢轮压路机采用高振频、低振幅振动的两遍压实时，其振动加速度值的平均值降低，但同样呈现出了随压实遍数的增加路面压实度随之增加的显著特点。

97、作为本发明的进一步方案，所述计算分析路面压实度与振动加速度有效值之间的实测关系，具体包括：

98、依托试验进程，按标准规定通过灌砂法取得该试验段芯样，测定其密度，并在对应点应用核子密度仪测出碾压位置的实际压实度；

99、此外，由于双钢轮压路机分别采用了低振频碾压和高振频碾压，除了碾压遍数的增加，压路机自身振动频率的变化也会使对应的振动加速度发生变化，最终所得的振动加速度有效值与实测压实度关系见表1所示；

100、

101、表1实测振动加速度有效值与实测压实度对照表

102、依据表1中数据获得的碾压作业过程中振动压实度与振动加速度关系，可以得知：

103、在低频振动下，将路面压实度与振动加速度之间关系式表示为：

104、y＝1.1957x-3.6182                      (24)

105、在高频振动下，将路面压实度与振动加速度之间关系式表示为：

106、y＝0.499x+63.36                        (25)

107、式中：y为压实度(％)；x为振动加速度有效值(m/s2)；

108、由此进一步可得，在不同的振动频率下，振动加速度有效值均随着路面压实度的增加而增加，具有良好的正向线性关系，且两者的相关系数分别为0.9563、0.9525，相关性良好；将其它采样数据代入这个关系式，经验证满足要求，故通过上述关系式代表该面层压实度与振动加速度有效值之间的关系。

109、作为本发明的进一步方案，还包括：

110、计算分析基于温度分布特性的压实度与振动加速度有效值关系。

111、作为本发明的进一步方案，所述计算分析基于温度分布特性的压实度与振动加速度有效值关系，具体包括：

112、采集沥青混合料碾压过程温降规律：

113、建立基于温度特性的压实度预测模型；

114、对于沥青混合料压实度-振动加速度-温度关系模型进行试验验证。

115、作为本发明的进一步方案，所述采集沥青混合料碾压过程温降规律，具体包括：

116、对于测试系统的终端采集仪传感器进行线性标定，并以此实时采集碾压过程中的路面温度，试验路段为单向三车道，由两台摊铺机以2.5m/min速度进行摊铺，成型厚度为6cm，考虑到沥青混合料内外温降速率的差异，由一测试人员手持插入式测温仪，以倾斜45°角测试距路面深度3cm处的混合料温度变化情况，获得的沥青混合料摊铺-碾压温降变化；

117、混合料摊铺碾压过程中路表温度和路面内部温度呈现出不同的变化特性，即，在路面内部温降基本表现为线性关系，而在摊铺表面，温度呈下凹抛物线式降低且其降温速度明显高于路面内部；此外，经摊铺机初始密实后，混合料在20min内下降速率最快，尤其在10min内，路表温度降温超过10℃；而在同样时间内，路面内部3cm处，降温仅2～3℃左右；

118、所述建立基于温度特性的压实度预测模型，具体包括：

119、碾压温度是沥青混合料压实过程的重要控制参数，按照实际施工中碾压温度选取165、155、145、135、125℃五种工况，对于不同碾压温度下，分别采集获得沥青混合料压实度与振动加速度的有效值，进一步测试五种碾压温度条件下，沥青混合料压实度与振动加速度有效值的关系，但在实际碾压过程中，沥青混合料的热量逐渐散失，温度不断下降；因此，基于此种状况，构建一沥青混合料压实度-振动加速度-温度关系模型的表达式：

120、k＝aebtα+ct+d                  (26)

121、式中：t为碾压温度，℃；a、b、c、d为拟合参数。

122、上述沥青混合料压实度-振动加速度-温度关系模型的拟合结果如下：

123、k＝0.697e0.009tα-0.462t+62.382，r2＝0.9921       (27)

124、由式(27)可知，沥青混合料压实度-振动加速度-温度关系模型的相关性系数r2＝0.9921，当碾压温度t取值为145～165℃范围内时，沥青混合料温度越高，内摩阻力越小，压实效果越好；以相同功碾压且达到同一压实度时，沥青混合料温度越高，振动加速度测试值越小；碾压温度165℃条件下的振动加速度比155℃条件下的振动加速度要小约1m/s2，155℃条件下的振动加速度比145℃条件下的振动加速度要小约2m/s2；

125、当碾压温度较低时，其对振动加速度的影响忽略不计。

126、作为本发明的进一步方案，所述对于沥青混合料压实度-振动加速度-温度关系模型进行试验验证，具体包括：

127、对压实后的沥青混合料中面层多点取芯，之后对取得芯样进行密度检验，并求取多个芯样的密度平均值，得到平均芯样密度为2.490g/cm3，而对应的该沥青混合料的毛体积密度为2.528g/cm3，压实度平均值为98.5％；

128、在中面层沥青混合料施工过程中，基于相应路段对压实作业的振动压路机振动轮的振动加速度进行检测，并按照上述沥青混合料压实度-振动加速度-温度关系模型进行预测，得到模型预测压实度数据；

129、基于测试路段按照规范进行10组芯样取样，检测取样密度并根据取样密度求得对应的压实度数据；

130、将该芯样取样求得的压实度数据与上述模型预测压实度对比；

131、若经对比两者的变化趋势最大偏差值低于要求值，则验证沥青混合料压实度-振动加速度-温度关系模型能够符合对于路段压实度的实时预测要求。

132、本发明具有如下有益效果：

133、该方法基于对传统压实度检测技术、压实度影响因素、及因压实质量不高引起路面病害的深入剖析，以保证后续路面的承载能力及使用寿命为目的，针对传统检测时样本量小、随机性大，以点代面，被动低效等不足，通过理论分析、仿真模拟、大数据解析与试验研究解决了在针对路面沥青混合料进行压铺筑实时，沥青混合料随其密实作用反馈的振动加速度信号会出现过增大，致使路面出现过碾压状态，进而导致大石料易被压碎，影响后续路面质量的问题。