一种面向高炉炼铁过程的时序核平稳宽度学习方法

本发明涉及一种面向高炉炼铁过程的时序核平稳宽度学习方法。

背景技术：

1、在有监督学习任务领域，研究人员已经推进了许多输入/输出样本建模的方法学。然而，在许多计算资源有限的环境中，特别是在现实世界的工业环境中，由于缺乏专门的计算服务中心，大量高性能深度学习模型的部署往往受到阻碍。

2、为了规避这一问题，从随机向量函数链路神经网络和极端学习机(extremelearning machine)中汲取灵感，设计出了广义学习系统(broad learning system，bls)。这种独特的网络扩大了广度，提高了计算效率，确保了模型性能。从本质上讲，这种三层前馈神经网络通过合并大量随机特征映射，避免了详尽的迭代反向优化过程，并通过回归估计确保最佳参数。自诞生以来，bls及其衍生物已被证明非常有效，并被广泛应用于各个领域，包括生物信息学、电力电子学、机器人学、道路交通和工业应用。

3、尽管bls变体经常被用于监督学习任务，但在错综复杂的情况下，特别是在非线性、时间错位、非平稳性和时间可变性等因素造成的情况下，仍有进一步研究时间序列建模和异常检测的明显需求。

4、基于bls的方法处理过程非线性的能力从根本上说与它形成的隐藏层有关，隐藏层由特征节点和增强节点组成，并由非线性激活函数激活。yu等人将bls与自动编码器框架和图正则化结合使用，从而获得了增强的特征表示估计。与此同时，feng和zou等人探索了t-s模糊系统，将映射特征节点替换为一组t-s模糊子系统。在引入小波bls时，lin等人使用小波函数来推导映射特征节点。然而，考虑到基于bls的本征随机非线性映射，生成足够数量的节点以实现充分可靠的非线性覆盖变得至关重要。因此，如果在随机非线性映射之前设置一个值得信赖的初始非线性探索，就能有效减少对后续节点的需求，为进一步研究更复杂的非线性特征铺平道路。

5、在时间表示方面，融合了递归神经网络和bls的功能后，就产生了递归-bls，它可以通过神经单元在连续时间步长内的迭代计算，有效地提取时间信息，取得了令人印象深刻的结果。在此基础上，通过加入适当的门控单元，门控-bls得以发展，进一步增强了其在时间序列建模方面的能力。peng等人有效地整合了残差机制和时滞概念，发展出时间堆叠广义学习系统(time-sbls)。该系统善于捕捉重要的非线性特征和时间相关性，从而提高了异常检测的精度。此外，zhong等人还巧妙地将时序记忆模块与双bls解码模块合并，建立了用于异常检测的记忆bls(memblsad)。然而，这些方法在面对模型输入与输出采样率不一致的多尺度采样(即时间错位情况)时显得力不从心。在某些情况下，可以利用下采样技术来强制输入和输出数据对齐，以进行模型拟合。然而，伴随下采样而来的大量信息丢失会明显降低模型性能。

6、非平稳性是现实世界数据的另一个常见特征，因此有必要考虑提高模型的泛化性能。当代一些研究人员利用去噪技术(如正则化)来减轻数据异常值造成的干扰。这自然引出了可以应用正则化理论的想法。因此，通过引入正则化项并将其与增强拉格朗日乘数相结合来增强模型对噪声的抵抗力，从而构建了l2rbls。此外，现有文献也强调了通过使用稀疏编码来增强模型鲁棒性的重要成就。但必须认识到，这种对过程噪声的探索只是过程非平稳性研究的一个子集，而过程非平稳性研究主要关注的是随时间变化的统计特性。遗憾的是，现有的bls方法并不能解决非平稳性问题。

技术实现思路

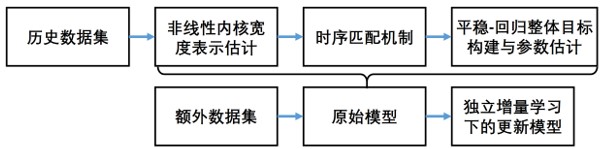
1、为了克服现有技术的不足，本发明提供一种时序核平稳宽度学习方法，步骤包括：非线性内核宽度表示估计、时序匹配机制、平稳-回归整体目标构建与参数估计以及独立增量学习。

2、本发明专门研究保证高炉炼铁过程的预测性能与故障监测能力。因此，本发明提出了一个回归建模和异常检测框架，该框架以时序核平稳宽度学习系统(tks-bls)为基础。首先，创建了一种非线性内核宽度表示(nonlinear kernel broad representation,nkbr)提取策略，通过内核技术为随机特征映射提供了稳健的非线性基础。随后，通过一个时间对齐参数来探究模型输入和输出之间的内部时序匹配机制，该参数可在潜在变量关系下进行解释。在整合阶段，本发明建立了一个基于kullback-leibler目标函数，以方便捕捉时间序列数据中的平稳关系并结合回归误差结合总体目标函数。最后，提出了一种双环参数优化算法和独立的增量学习机制，两者都有全面的理论分析作为支持。

3、一种时序核平稳宽度学习系统，步骤包括：非线性内核宽度表示估计、时序匹配机制、平稳-回归整体目标构建与参数估计以及独立增量学习。

4、所述的非线性核宽度表示包括如下步骤：

5、(2.1)针对高炉炼铁过程中的复杂，所述的tks-bls方法首先开发了一个基于核的非线性特征提取器；为了应对非线性首先采用了核方法，其中映射函数φ(.)将数据x(·)从原始空间投影到高维特征空间

6、

7、fori,j＝1,2,…,n(1b)

8、式中，κ(.)代表特定的核函数以及定义为空间中的内积运算，而中心化则通过以下方式计算获得：

9、

10、其中，in的所有元素都设为1/n。要深入研究核函数对非线性信息的影响，必须指定一个特定的核函数。在本分析中，以高斯核为代表，其可表述如下：

11、

12、式中，γ为核宽度。以下式(4)始终成立，即

13、

14、通过引入泰勒展开式，可以得出

15、

16、因此，非线性映射φ(x(i))可明确表示为

17、

18、通过式(6)，高斯核函数有助于探索数据中的高阶非线性关系。显然，这种方法也有助于使用其他核函数(如多项式核函数和拉普拉斯核函数)检验非线性信息的提取能力。

19、(2.2)然而在核函数映射之后，数据矩阵的大小会从到与n＞＞kx有相当大的扩展。这种显著的扩展将明显增加后续程序的计算需求。为了解决这个问题，我们采用了主成分分析法(pca)来保留的基本信息，其表达式如下：

20、

21、其中对角矩阵ξ＝diag(ξ1,ξ2,…,ξn)由特征值组成，并v＝[v1,v2,…,vn]由相应的特征向量构造而成。最大的d(d<n)特征值连同各自的特征向量构成非线性核表示(nkr)其缩小矩阵为vd＝[v1,v2,…,vd]。值得强调的是，pca的应用不仅大大减小了nkr矩阵的大小，还能通过丢弃残余子空间来有效过滤系统噪声。这一关键过程可防止噪声在随后的非线性核宽表示(nkbr)提取过程中积累。

22、(2.3)这里以nkr t为基础，参照宽度映射机制构建相应的隐层，即nkbr

23、

24、其中mt特征节点和lt增强节点。

25、所述的时序匹配机制包括如下步骤：

26、(3.1)当系统的输入-输出变量之间的采样率存在显著差异时，就需要收集数据集其中包括n＝ns>n。每个输出采样y(i)与按时间s分级的输入采样z(i)＝[xt(i,1),xt(i,2),…,xt(i,s)]t.这种情况符合特定的性质：1、在最大时滞标度(以q表示)之后，输入将失去与输出的对应映射。此外，不同输出样本对应的输入样本不会相互重叠，即q小于s。2：在稳定系统中，所有输出样本y(i)的最大滞后标度q保持一致。

27、对nkbr z(i)的投影，给定为最大时滞标度q，可表示为考虑到潜变量形式，y(i)和aq(i)的投影向量分别表示为q和w，从而可以得出：

28、c(i)＝yt(i)q(9a)

29、t(i)＝aq,t(i)w(9b)

30、这里，为了进一步确认每个时滞标度与输出样本之间的配准关系，引入了一个配准参数β＝[β1,β2,…,βq]t。因此，对于每个y(i)，其潜在变量与输入样本的关系可表示为

31、

32、其中，β⊙w是β和w之间的矩阵kronecker积。根据这些定义

33、

34、

35、式(10)可以矩阵形式重构为

36、

37、(3.2)因此，整体目标的第一部分可以表述为最大化以下内容：

38、

39、注意的是，这种等价关系的出现源于这样一个概念，即最大化协方差与最小化预测值和观测值之间的差异同义。

40、所述的平稳-回归整体目标构建与参数估计包括如下步骤：

41、(4.1)为了有效解决高炉炼铁过程中的复杂混合过程，必须挖掘平稳性，从而减轻非平稳因素的影响。这就要求提取nkbr必须保持其一致性，表现为其均值和方差在不同时期的稳定性。当被分割成ε个时间段时，相应的均值和方差(μe,σe)应与总体均值和方差一致。为此，我们利用kl散度进一步构建总体目标的第二段即平稳目标，其计算公式为

42、

43、然而，直接最小化会导致对β和w的非凸优化问题。虽然某些研究利用梯度下降来解决这一问题，但它往往会消耗大量计算资源。为了减轻计算负担，我们将优化问题式(14)重构为二次目标，即：

44、

45、其中

46、

47、通过使用权衡参数η合并第一和第二部分，总体目标可表述为：

48、

49、s.t.qtq＝1,(β⊙w)t(β⊙w)＝1(17b)

50、(4.2)为了解决式(17)中的优化问题，需要使用拉格朗日乘子。定义拉格朗日函数

51、

52、其中拉格朗日乘数为λq和λw。分别对q,β,w,λq,和λw对上式(18)求导数并置零，可得

53、

54、

55、

56、

57、

58、将公式(19a)和(19b)的左边分别乘以qt和wt，可以计算出它们之间的关系为

59、

60、

61、在qtq＝1和(β⊙w)t(β⊙w)＝1的条件下，得出2λ＝λq+λw。因此，通过分别最大化λq和λw可以达到式(18)的目标。根据式(19)，q,β和w的值可由以下公式确定

62、

63、

64、

65、其中，∝表示两边的比例关系，表示伪逆算子。显然，从式(21)中可以看出，向量q,w和β的解相互交织，缺乏紧凑的形式。因此，tks-bls的结构可以通过迭代式(21)得到。

66、(4.3)随后，通过收集所有潜变量负荷向量投影向量从中可提取的潜变量为：

67、

68、随后，可以通过多元最小二乘法(即利用回归参数ζ)建立和之间的联系：

69、

70、其中表示对的回归估计，表示回归误差。正则化项θ用于减小潜在的病态矩阵的影响。最终，预测值和都可以直接从得出，即

71、

72、(4.4)对于及时建模与异常检测策略部分，收集q个输入样本后，可以建立新的观测输入样本，记为xnew＝[xt(new,1),xt(new,2),…,xt(new,q)]t。这样就可以计算出实时中心化均值核矩阵连同负载矩阵v，主要信息聚合的nkr可表示为：

73、

74、那么，对于t＝1,2,…,q，nkbr为

75、

76、通过汇总这些nbkr向量a(new,t)，可以利用滞后项aq,new和相应的潜变量τnew对输出变量进行实时预测：

77、

78、在异常检测方面，由于hotelling'st2统计量具有极高的灵敏度，因此在这里得到采用：

79、

80、相应的阈值jth遵循分布，στ代表的协方差矩阵，如式(28)所示，置信度用α表示。结合前面的说明和分析，接下来的异常检测逻辑表述为

81、

82、所述的独立增量学习包括如下步骤：

83、(5.1)通过开发优化目标和迭代算法，tks-bls具备了对具有时间错位的非线性、非稳态系统进行建模和异常检测的能力。然而，系统的时间可变性对于保持模型的有效性至关重要，因此必须具有可扩展性。因此，通过收集额外样本tx＝ns+1,ns+2,…,n+ds,ty＝n+1,n+2,…,n+d，建立了独立的增量学习技术。通过应用xc和yc可以构建相关的附加滞nkbr根据原始的tks-bls模型，式(8)有助于原始潜变量的计算。这也可以通过原始tks-bls模型定位和并将未建模残差表示为和

84、

85、式(30)表明和包含未建模的信息。由于系统的时变特性，这些元素包含了训练集中不存在的补充数据，因此有必要进行额外建模。为了研究原始模型对近期数据特征的忽略，本发明建立了一个辅助tks-bls模型：

86、

87、s.t.qc,tqc＝1,(βc⊙wc)t(βc⊙wc)＝1(31b)

88、其中

89、

90、对lc投影向量的进一步估计会挖掘额外的潜变量并通过以下方法将每个潜变量与其预测值配对

91、

92、其中，和是负载矩阵，ζc是回归矩阵。然后，将初始模型和更新模型的回归建模能力综合起来，就可以由aq,new给出出整个系统的综合表示，即

93、

94、将原始模型和更新模型中的潜变量依次排列为即可得到改进的hotelling'st2统计量：

95、

96、

97、其中矩阵的协方差用表示，如式(28)所示。分布设定的相应临界值用表示。值得注意的是，所提出的独立增量学习可以确保额外的潜变量与原始变量保持不同。这就保持了原始模型和补充模型之间的正交性，表明没有性能干扰或重叠。原始训练数据通常反映了系统的长期特征，而额外的数据则捕捉了近期的趋势。这种混合增强了对更全面的潜在变量的估计，并提高了回归建模能力。

98、本发明的有益效果：

99、首先，采用核函数和宽度学习方法，建立了一个挖掘丰富非线性特征结构。接下来，构建利用时序配准参数对齐了采样率失配下的输入与输出变量，并构建了结合平稳性与回归特性的整体优化目标，并利用循环缩放就行求解。随后，独立增量学习策略被构造以克服过程的时变特性。此外，本发明的案例研究表明，提出的tc-glnassa在提高高炉炼铁预测与过程效果，保障设备安全运行方面迈出了重要一步。