一种测量I型内聚力本构关系的试验方法

本发明涉及工程材料力学性能测试领域，涉及但不限定于一种测量i型内聚力本构关系的试验方法。

背景技术：

1、目前关于断裂的研究和测试大多假设断裂过程为线弹性，然而实际上很多裂纹尖端前部存在大范围塑性区，如图1左侧部分，因此表征塑性断裂过程是极其重要的。内聚力模型（cohesive zone model，czm）是表征界面断裂行为的重要理论，其本构关系为牵引分离定律（traction-separation law，tsl），即内聚力本构关系，如图1右侧部分。内聚力模型可广泛应用于分析韧性胶结界面开裂、复合材料界面的桥联效应，热塑性复合材料焊接界面开裂等领域。能够准确快速获得其断裂韧性和内聚力本构关系对实际应用具有重要意义。

2、目前测量tsl的方法包括反方法（inverse method）和直接法（direct method）等。反方法中需要预设tsl的形状，通过结合有限元进行不断迭代计算直至匹配试验数据，比如载荷-位移曲线。这种方法依据经验可确定部分材料的tsl形状，但是提前定义tsl的形状仍然会引入误差。相比于通用的tsl形状，比如双线性、梯形、指数等形式，直接测量的tsl具有更准确的结果。直接法利用断裂能对裂纹尖端分离的微分计算牵引力进而构建得到tsl，但是断裂能的数据缩减方法和微分方法仍会对结果带来误差。

技术实现思路

1、有鉴于此，本发明实施例提供一种测量i型内聚力本构关系的试验方法，旨在提出一种可以基于欧拉梁理论计算韧性界面牵引力和分离的方法以更精确快速实现韧性界面i型开裂的tsl表征。

2、本发明实施例的技术方案是这样实现的：

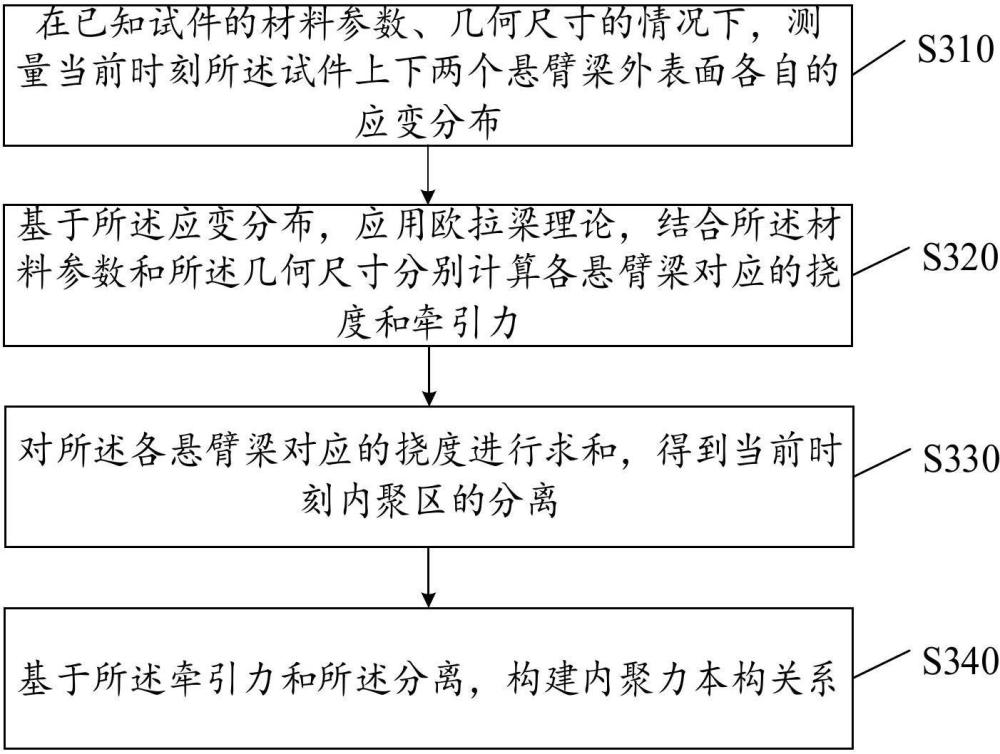
3、本发明实施例提供一种测量i型内聚力本构关系的试验方法，所述方法包括：

4、在已知试件的材料参数、几何尺寸的情况下，测量当前时刻所述试件上下两个悬臂梁外表面各自的应变分布；基于所述应变分布，应用欧拉梁理论，结合所述材料参数和所述几何尺寸分别计算各悬臂梁对应的挠度和牵引力；对所述各悬臂梁对应的挠度进行求和，得到当前时刻内聚区的分离；基于所述牵引力和所述分离，构建内聚力本构关系。

5、在一些可能的实施例中，所述材料参数包括弯曲模量；所述基于所述应变分布，应用欧拉梁理论，结合所述材料参数和所述几何尺寸分别计算各悬臂梁对应的牵引力，包括：应用欧拉梁理论，结合所述弯曲模量和截面惯性矩确定相应悬臂梁的弯矩分布；其中，所述截面惯性矩由所述几何尺寸确定；基于所述弯矩分布和所述应变分布，确定所述悬臂梁上的拉伸力；基于所述拉伸力和所述几何尺寸，确定所述悬臂梁上的牵引力。

6、在一些可能的实施例中，所述几何尺寸包括悬臂梁的宽度和厚度，通过以下公式计算各悬臂梁对应的挠度：

7、；

8、；

9、<mstyle displaystyle="true" mathcolor="#000000"><mstyle displaystyle="true" mathcolor="#000000"><mi>w</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>(</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>x</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>)</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>=</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mstyle displaystyle="true"><msubsup><mo>∫</mo><mn>0</mn><mi>x</mi></msubsup><mstyle displaystyle="true"><msubsup><mo>∫</mo><mn>0</mn><mi>x</mi></msubsup><mrow><mstyle displaystyle="true" mathcolor="#000000"><mi>[</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>−</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mfrac><mstyle displaystyle="true" mathcolor="#000000"><mstyle displaystyle="true" mathcolor="#000000"><mn>2</mn></mstyle></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mstyle displaystyle="true" mathcolor="#000000"><mi>h</mi></mstyle></mstyle></mfrac></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>ε</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>(</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>x</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>)</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>]</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>d</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>x</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>d</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>x</mi></mstyle></mrow></mstyle></mstyle></mstyle></mstyle>；

10、其中，为依据欧拉梁理论，试件弯曲的轴向正应变分布；x为中心轴方向变量，z为原点在中心轴上沿着垂直轴方向的坐标，为挠度，为悬臂梁外表面的应变分布；h为悬臂梁的厚度。

11、在一些可能的实施例中，通过以下公式计算所述各悬臂梁对应的牵引力：

12、；

13、；

14、；

15、其中，为悬臂梁的弯矩分布，e为悬臂梁的弯曲模量，i = bh3/12为截面惯性矩，b为悬臂梁的宽度，h为悬臂梁的厚度，为挠度；为悬臂梁外表面的应变分布；为分布于悬臂梁上的拉伸力；为悬臂梁的牵引力。

16、在一些可能的实施例中，所述方法还包括：基于所述各悬臂梁对应的牵引力分析得到韧性界面的应力分布；通过应力为0的位置推算裂尖的位置；通过所述应力分布推算裂尖到最大牵引力的距离，得到内聚区长度。

17、本发明实施例提供的技术方案带来的有益效果至少包括：

18、在本发明实施例中，仅需要采集断裂中某时刻试件外表面的应变分布，然后基于以上欧拉梁模型进行牵引力和挠度的计算，计算过程更为简单高效。从而避免了测试过程中的裂纹长度和裂纹尖端分离的采集，同时避免了长时间的数据采集，计算过程更为简单高效，实现更精确快速的tsl表征。