一种切换通信拓扑下的非线性系统自适应协同控制方法与流程

本发明属于非线性系统的协同控制，其针对严格反馈的非线性系统的分布式自适应协同控制领域，具体涉及一种切换通信拓扑下的非线性系统自适应协同控制方法。

背景技术：

1、在生产生活中，目前常用的控制方法是将物理系统简化为参数完全已知的线性系统，从而便于设计线性二次型调节(linear quadratic regulator，lqr)控制器或模型预测控制(model predictive control，mpc)控制器。而有的控制器则是不考虑物理系统的数学模型，通过不断测试控制参数，来实现对物理系统的控制，比如典型的比例-积分-微分(proportional-integral-derivative，pid)控制器。然而，大部分物理系统在工程应用时会存在非线性特征，且系统的某些物理参数难以测量，甚至可能随时间发生改变。因此，基于线性化且完全已知的系统模型进行控制或者黑箱pid控制，都难以适应系统的动态变化，导致无法长时间保证系统性能。

2、此外，随着工业系统智能化程度以及工业任务复杂度的提升，协同作业的需求日益增加。为了实现协同作业，系统之间需要进行信息交互。目前，最方便快捷的信息交互方式包括蓝牙、局域网等无线电手段。然而，这些方法容易受到干扰、外部攻击的影响，存在一定的安全隐患。而跳频技术则提供了相应的解决方案。通过利用该技术，可以为采用不同的载波频率或者是加密密钥对通信信道进行切换，进而提高通信对干扰和攻击的抵抗能力。然而，在实际应用中，信道切换的不同步给系统的稳定性带来了负面的影响，增加了协同控制器的设计难度。

技术实现思路

1、(一)要解决的技术问题

2、本发明要解决的技术问题是：如何提出一种切换通信拓扑下的非线性系统自适应协同控制方法。

3、(二)技术方案

4、为解决上述技术问题，本发明提供一种切换通信拓扑下的非线性系统自适应协同控制方法，所述方法包括以下步骤：

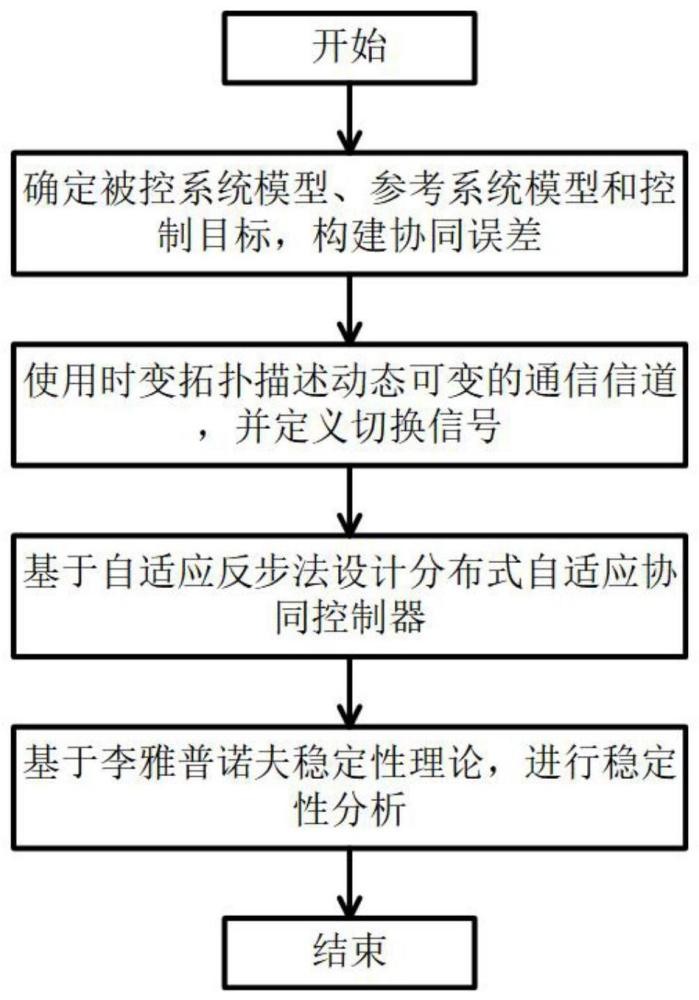
5、第一步，确定被控系统模型、参考系统模型和控制目标，并利用被控系统的状态和参考系统的状态定义协同误差变量；

6、第二步，使用时变拓扑描述动态可变的通信信道，并定义切换信号；

7、第三步，基于自适应反步法设计分布式自适应协同控制器；

8、第四步，基于李雅普诺夫稳定性理论，进行稳定性分析，确定闭环系统的有界性。

9、其中，所述第一步中，被控系统模型如下：

10、

11、

12、式中，和是系统i的状态变量，xi＝[xi,1,xi,2]t，是控制输入，φi,z(·):是光滑的非线性函数，z＝1,2，ri是正整数，是未知的常数向量，n表示非线性系统的个数。

13、其中，所述第一步中，参考系统模型如下：

14、

15、

16、式中，和是参考系统的状态变量，φr(xr):是光滑的非线性函数，xr＝[xr,1,xr,2]t。

17、其中，所述第二步中，设计切换信号时，保证在任意时刻，均存在一个以参考系统为根节点的有向生成树，使得存在路径从根节点抵达任意一个系统节点。

18、其中，所述第二步中，根据非线性系统的个数，估计全局拓扑参数的上界，具体估计方法如下：

19、

20、

21、

22、式中，n表示非线性系统的个数，χ为正整数，表示全局拓扑参数pi的上界，i的取值为1、2、...、χ、χ+1、χ+2、...、n。

23、其中，所述第二步中，使用时变的有向拓扑描述系统间动态可变的通信信道，其中，v＝{1,2,...,n}表示每个系统对应的索引集，表示不同系统之间通信通道的集合；假设有向图g(t)包含一棵以参考系统为根节点的生成树，在该生成树中，存在路径从根节点抵达任意一个系统节点；λ中的元素表示为(i,j)，i,j∈v，通道(i,j)表示系统j可以从系统i获取状态信息；此时，称系统i为系统j的邻居；如果在时刻t有(j,i)∈λ和则分别定义aij(t)＝1和aij(t)＝0；系统i邻居的索引下标构成集合ni；其中，不考虑系统与自身进行通信，即不存在通信通道(i,i)，aii(t)＝0；

24、所述第三步中，误差变量定义为：

25、

26、

27、ei,2＝xi,2-αi,

28、

29、式中，i和j均为索引下标，分别表示系统i和j，是系统i使用的对xr,1的估计值，αi是系统i使用的虚拟控制量，xj,1表示系统的状态，ρi表示为系统预设的协同偏差。

30、其中，所述第三步中，分布式自适应协同控制器设计为：

31、

32、

33、式中，ci,1、ci,2、ci,4、γi,1、κi,1和xi,r,0是正常数，是对参数pi的上界的平方的估计值，是系统i使用的θi的估计值，和分别是αi对xi,1、和的偏导数。

34、其中，所述第三步中，参数自适应律设计为：

35、

36、

37、τi＝γi,3φi,1ei,1,

38、

39、

40、式中，τi和ζi是系统i使用的中间变量，ci,3、γi,2、κi,3和θi,0是正常数，γi,3是正定对角矩阵，proj(ζi)是投影算子。proj(ζi)的具体形式如下：

41、

42、式中，β是正常数，和pi分别是估计值的上界和下界，且均大于0；该投影算子可以保证

43、其中，所述第四步中，李雅普诺夫函数选取为：

44、

45、式中，

46、其中，所述方法基于被控对象和参考系统的模型，定义协同误差；采用时变有向拓扑描述非线性系统之间的动态有向通信，然后设计分布式自适应协同控制器，并分析闭环系统的有界性；所设计的控制器解决了传统控制方法无法完全分布式运行、无法处理未知参数以及要求时变拓扑的切换驻留时间必须存在严格正下界的问题，可用于任意规模且通信拓扑时变的多智能体系统，具有更强的实用性和可靠性

47、(三)有益效果

48、与现有技术相比较，本发明基于被控对象和参考系统的模型，定义协同误差；采用时变有向拓扑描述非线性系统之间的动态有向通信，然后设计分布式自适应协同控制器，并分析闭环系统的有界性。所设计的控制器解决了传统控制方法无法完全分布式运行、无法处理未知参数以及要求时变拓扑的切换驻留时间必须存在严格正下界的问题，可用于任意规模且通信拓扑时变的多智能体系统，具有更强的实用性和可靠性。

49、本发明的特点以及有益效果是：

50、(1)利用本发明提出的一种切换通信拓扑下的非线性系统自适应协同控制方法，针对一类严格反馈的非线性系统，可以实现对参考系统状态的分布式协同跟踪；

51、(2)本发明可以应用于任意规模大小的群体系统，避免了控制输入上下界随规模增大而增大的情况；

52、(3)本发明可在切换驻留时间任意小的切换通信拓扑下实现协同控制，适用于信道切换且无法精确同步的应用环境；

53、(4)本发明应用自适应技术自动调整控制器增益，不需要精确获取被控系统的系统参数，便于工程实现；

54、(5)本发明可以通过调整控制器参数，减小协同误差。