六轴振动台的解耦控制方法及系统

本发明属于实时控制领域，具体涉及一种六轴振动台的解耦控制方法及系统。

背景技术：

1、实时混合试验（real-time hybrid simulation，rths）是结构抗震领域的重要试验方法。rths将结构分为物理子结构和数值子结构，其中物理子结构包含结构中难以建模、特性复杂或需要进行试验测试的部分，数值子结构包含结构中易于建模、不便于试验或研究成熟的部分。在物理子结构中，加载信号由数值子结构实时计算，并通过振动台实时加载；数值子结构根据试件反馈的信号计算下一时刻的加载信号。具体实施时，振动台对于加载信号的复现精度，比如时滞、均方根误差和峰值误差等，很大程度上影响了rths的稳定性和精度。

2、对于单一试件或单一工况，传统的pid控制、三参量控制及模型预测控制等控制方案，在专门整定后都能够取得良好的效果。但是，这些方案均假设控制台是线性时不变系统，基于特定频率、加载和试件的假设进行控制方案合计，忽略了振动台的不确定性以及试件对振动台特性的影响。这使得该类方案在对振动台进行实际控制时，确实存在可靠性差、精确性差的问题。

3、此外，在加载不同频段的波形时，振动台会出现不同程度的耦合效应，且耦合程度随波形震动的频率及幅值增大而增大。传统的解耦控制方案在设计过程中，要求对被控对象进行完全建模；但是，完全建模的要求在实际过程中极难实现。因此，现有的解耦控制方案并不能有效的解决这类问题。

技术实现思路

1、本发明的目的之一在于提供一种可靠性高且精确性好的六轴振动台的解耦控制方法。

2、本发明的目的之二在于提供一种实现所述六轴振动台的解耦控制方法的系统。

3、本发明提供的这种六轴振动台的解耦控制方法，包括如下步骤：

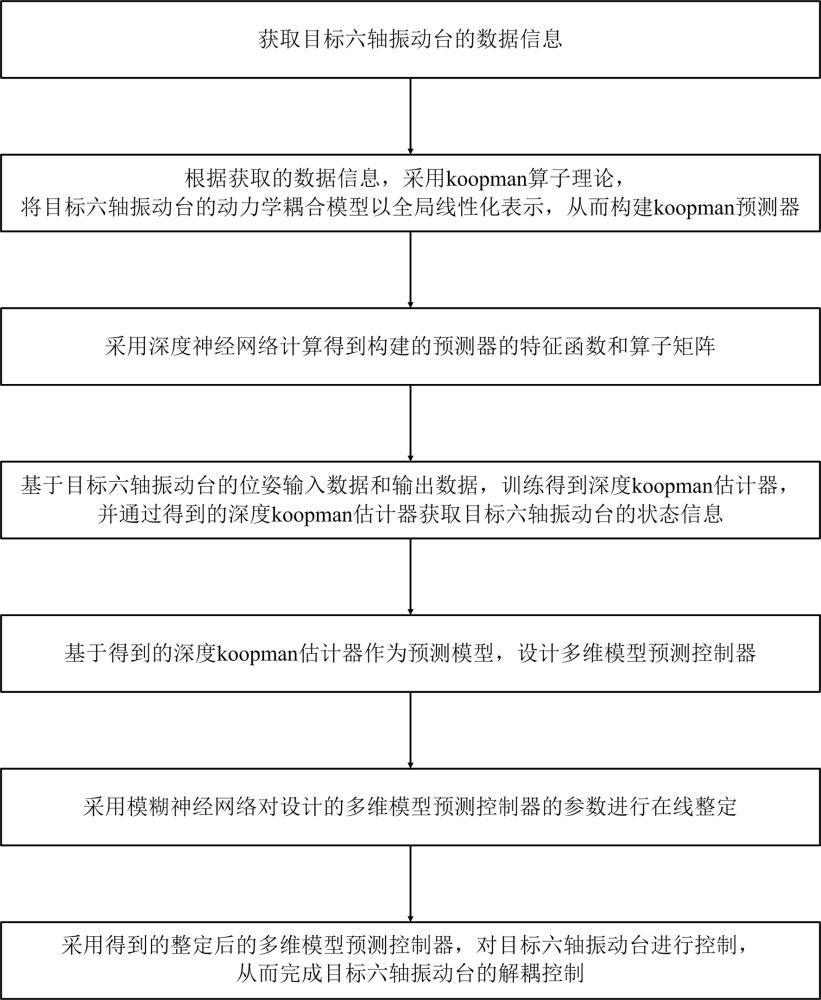
4、s1. 获取目标六轴振动台的数据信息；

5、s2. 根据步骤s1获取的数据信息，采用koopman算子理论，将目标六轴振动台的动力学耦合模型以全局线性化表示，从而构建koopman预测器；

6、s3. 采用深度神经网络计算得到步骤s2构建的预测器的特征函数和算子矩阵；

7、s4. 基于目标六轴振动台的位姿输入数据和输出数据，训练得到深度koopman估计器，并通过得到的深度koopman估计器获取目标六轴振动台的状态信息；

8、s5. 基于步骤s4得到的深度koopman估计器作为预测模型，设计多维模型预测控制器；

9、s6. 采用模糊神经网络对步骤s5设计的多维模型预测控制器的参数进行在线整定；

10、s7. 采用步骤s6得到的整定后的多维模型预测控制器，对目标六轴振动台进行控制，从而完成目标六轴振动台的解耦控制。

11、所述的步骤s2，包括如下步骤：

12、设定目标六轴振动台的位姿动力学模型；在位姿动力学模型中，引入koopman算子，构建得到koopman预测器，用于将目标六轴振动台的非线性模型升维到线性空间，进而得到目标六轴振动台的动力学模型的线性化表达。

13、所述的步骤s2，具体包括如下步骤：

14、设定目标六轴振动台的位姿动力学模型为：式中为k+1时刻的位姿向量；为k时刻的位姿向量；为k时刻的控制向量；为状态到状态的非线性映射函数；

15、的表达式为，其中为k时刻目标六轴振动台的x轴方向的位姿，为k时刻目标六轴振动台的y轴方向的位姿，为k时刻目标六轴振动台的z轴方向的位姿，为k时刻目标六轴振动台绕x方向旋转的位姿，为k时刻目标六轴振动台绕y方向旋转的位姿，为k时刻目标六轴振动台绕z方向旋转的位姿；

16、的表达式为，其中为位姿在k时刻的控制信号，为位姿在k时刻的控制信号，为位姿在k时刻的控制信号，为位姿在k时刻的控制信号，为位姿在k时刻的控制信号，为位姿在k时刻的控制信号；

17、预测时步的控制信号通过计算得到并设定其保持不变；定义有限维的koopman算子矩阵和位姿的观测函数矩阵，满足式中表示k时刻的位姿观测函数矩阵，且

18、，为表示位姿在升维后的观测函数，，h为无穷希伯尔特空间，取值为 x、 y、 z、、或；a为升维系统的系统矩阵，且，为对应的系统矩阵；b为升维系统的输入矩阵，且，为对应的输入矩阵；

19、k时刻和k+1时刻的观测函数矩阵通过有限维的koopman算子矩阵 k在 h空间演进，koopman算子矩阵 k能够将位姿状态对应的六自由度振动台非线性模型升维至 h空间，koopman算子矩阵 k对应的表达式为式中为位姿在升维后对应的koopman算子。

20、所述的步骤s3，具体包括如下步骤：

21、通过深度神经网络拟合位姿观测函数矩阵和算子矩阵 k；

22、其中，第一深度神经网络用于拟合位姿观测函数矩阵；第二深度神经网络用于拟合位姿观测函数矩阵的反函数，实现位姿模型的升维以及降维，并通过线性准则确定算子矩阵 k；基于深度神经网络的表示为基于，将位姿的非线性模型以升维的线性状态矩阵表示；升维后的状态通过 k演进，基于演进后的状态、输入和得到下一时刻的状态向量的估计值，表示为：

23、式中为位姿在时刻的估计值；为位姿在时刻的估计值；为位姿在时刻的估计值；为位姿在时刻的估计值；为位姿在时刻的估计值；为位姿在时刻的估计值。

24、所述的步骤s4，具体包括如下步骤：

25、基于目标六轴振动台的位姿输入数据、控制信号和输出数据，训练得到和，从而确定从原始状态和输入到koopman不变子空间下的映射、线性动力系统和从不变子空间到原始状态的映射；

26、设计网络的准则函数为：

27、

28、式中表示求范数操作；

29、koopman预测器的输入和深度神经网络的输入均为六轴振动台的六个位姿，的输出为六轴振动台的六个位姿的估计值。

30、所述的步骤s5，具体包括如下步骤：

31、将多维模型预测控制初步模型的预测问题，描述为如下优化问题：

32、

33、式中为位姿的代价函数，取值为 x、 y、 z、、或；和分别为系统的预测时域和控制时域；为位姿在 k+ s时刻的预测值；为求权重为的范数的符号；为求权重为的范数的符号；为位姿在 k+ s时刻的参考输入；为位姿在 k+ s时刻输入信号的增量；为控制矩阵的下限；为控制矩阵的上限；

34、优化过程中，设定在控制时域之外的控制量保持不变；每一个优化问题的和均保持相同。

35、所述的步骤s6，包括如下步骤：

36、步骤s5设计的多维模型预测控制初步模型的参数包括、和；

37、针对参数和，采用经验法进行整定计算；

38、针对参数，采用模糊神经网络进行实时整定。

39、所述的针对参数，采用模糊神经网络进行实时整定，具体包括如下步骤：

40、采用的模糊神经网络包括输入层、隶属度函数层、模糊规则适应度层、归一化层和网络输出层；

41、网络输出层的输出为参数的增量，且；n为模糊神经网络的规则数；为位姿对应的第 kk个规则的输出权重；为归一化层对应的输出；

42、然后，计算得到增益的更新率为；

43、设定模糊神经网络的性能指标函数为式中为期望值，为k时刻的目标值；为k时刻的实际输出值；

44、基于性能指标函数，采用梯度下降算法对模糊神经网络的相关参数更新；更新过程表示为式中为参数在t+1时刻的取值；为参数在t时刻的取值；为学习率；为平滑因子。

45、本发明还提供了一种实现所述六轴振动台的解耦控制方法的系统，包括数据获取模块、预测器构建模块、预测器计算模块、状态信息计算模块、模型设计模块、模型训练模块和解耦控制模块；数据获取模块用于获取目标六轴振动台的数据信息，并将数据信息上传预测器构建模块；预测器构建模块用于根据接收到的数据信息，根据获取的数据信息，采用koopman算子理论，将目标六轴振动台的动力学耦合模型以全局线性化表示，从而构建koopman预测器，并将数据信息上传预测器计算模块；预测器计算模块用于根据接收到的数据信息，采用深度神经网络计算得到构建的预测器的特征函数和算子矩阵，并将数据信息上传状态信息计算模块；状态信息计算模块用于根据接收到的数据信息，基于目标六轴振动台的位姿输入数据和输出数据，训练得到深度koopman估计器，并通过得到的深度koopman估计器获取目标六轴振动台的状态信息，并将数据信息上传模型设计模块；模型设计模块用于根据接收到的数据信息，基于得到的深度koopman估计器作为预测模型，设计多维模型预测控制器，并将数据信息上传模型训练模块；模型训练模块用于根据接收到的数据信息，采用模糊神经网络对设计的多维模型预测控制器的参数进行在线整定，并将数据信息上传解耦控制模块；解耦控制模块用于根据接收到的数据信息，采用得到的整定后的多维模型预测控制器，对目标六轴振动台进行控制，从而完成目标六轴振动台的解耦控制。

46、本发明公开的这种六轴振动台的解耦控制方法及系统，通过深度学习算法拟合耦合特征，进而通过所估计的位姿信号对不同位姿进行分离设计，使用六个模型预测控制完成六轴振动台的位姿模型预测控制；最后，本发明还通过模糊神经网络实时调节模型预测控制的权重参数，使得本方案能够根据具体情况进行实时调节，增强了系统的鲁棒性；因此，本发明的可靠性更高，而且精确性更好。