一种强鲁棒性的AUV分数阶滑模控制方法

本发明专利涉及auv的控制领域，尤其是一种强鲁棒性的auv分数阶滑模控制方法。

背景技术：

1、随着人类对海洋探索的越发深入，人类越发需要一种可以在水下不需要电缆自主行动的航行器。auv正是为了满足这一要求而诞生的。自auv诞生以来，跟踪一直是auv的热门研究课题之一。跟踪问题主要包含轨迹跟踪和路径跟踪，两者的区别是是否与时间有关，前者有着较强的时间约束。而本发明主要针对的就是轨迹跟踪。

2、auv的数学模型较为复杂，auv动力学具有高度非线性耦合的特点，而海洋环境中的不确定性也增大了auv的控制难度。auv在水下具有六个自由度，这就代表auv要控制纵向速度、横向速度、升沉速度、横倾角速度、纵倾角速度与艏向角速度六个方向上速度的稳定性。而滑模控制作为一种特殊的非线性控制,因其具有应用简单，鲁棒性好等特点，非常适合用来设计auv的控制系统。

3、同时auv分为全驱动型和欠驱动型，欠驱动既作为大多数auv根据能耗载荷等实际情况所选择的配置，而全驱动auv也要考虑在部分执行机构失效的情况下如何完成任务或者稳定回收，所以针对欠驱动auv设计稳定和可靠的控制器是十分有必要的。

4、对于现有auv滑模控制的研究成果进行检索，发现众多学者根据需求设计了基于传统滑模、积分滑模、终端滑模。但这些控制系统依旧存在着或多或少的问题，其中最突出的就是抖振问题。因为滑模是变结构控制，所以抖振常常是改进滑模控制最优先解决的问题。常见的解决方法有将趋近率中的符号函数改为连续的饱和函数或者是双曲正切函数等，大多数都是从趋近率的角度去减少抖振的产生，而很少有从滑模面的角度去进行改进。同时虽然滑模控制本身就是鲁棒性较强的控制方法，但是应用中只能抵抗较小的扰动，对与大多数文献中以及本人之前研究所设计的控制系统而言，如果干扰过大就会产生无法跟踪或者跟踪轨迹不稳定的现象。而在无人机等领域，滑模的改进形式更加多样，其中不乏使用分数阶来减弱滑模算法的抖振，提高控制的抗干扰效果，但大多数设计的干扰都是轻微的动态扰动，在这些扰动的作用下对比算法也仅是出现抖动或是跟踪不稳定的现象，而没有出现完全无法跟踪的情况。海洋环境更加复杂，auv可能面临强扰动的环境，因此设计能够在强干扰作用下依旧可以稳定轨迹跟踪的控制器至关重要。为了解决这些问题本发明从控制框架、滑模面以及趋近率三个角度结合设计了一种控制系统，在考虑外部存在剧烈扰动的情况下，设计双闭环的控制系统，同时将分数阶引入滑模面中，分数阶是一种带有记忆性质的数学方法，其计算方法涉及之前多个时间段的信息，这大大增强了系统的抗干扰能力，同时将趋近率设计为二阶趋近率削弱了抖振的发生。之后设计观测器进一步加强整个控制系统的稳定性，保证执行器输出的稳定。

技术实现思路

1、针对上述问题，本发明提出一种强鲁棒性的auv分数阶滑模控制方法，

2、这种方法能够使得auv具有较强抗干扰能力，且快速收敛的同时能够避免明显抖振的产生。方法主要包括如下步骤：

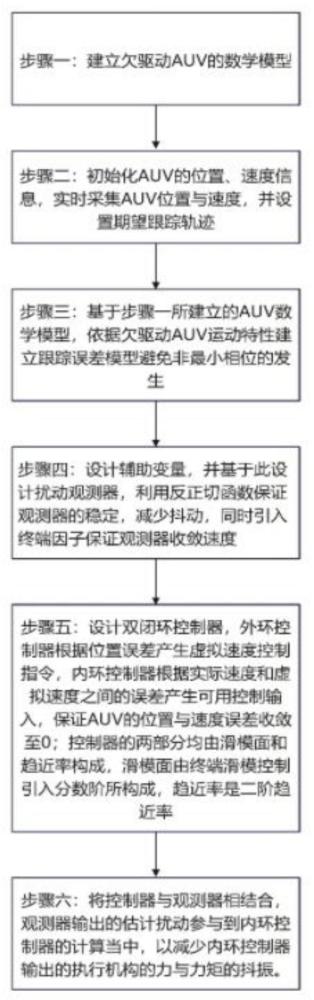
3、1、步骤一：建立auv数学模型；

4、auv的数学模型由运动学模型与动力学模型构成用矩阵向量可以表示为：

5、

6、其中η＝[x,y,z,φ,θ,ψ]t表示惯性坐标系下auv的位置和姿态；v＝[u,v,w,p,q,r]t表示auv在载体坐标系下的速度矢量，其参数分别表示auv的纵向速度、横向速度、升沉速度、横倾角速度、纵倾角速度与艏向角速度；m表示含有附加质量的惯性矩阵；c(v)是表示离心力与科氏力的矩阵；d(v)表示非线性水动力阻尼矩阵；g(η)表示auv在水中的重力与浮力相互作用形成的恢复力与力矩的矩阵；τ＝[τu,0,0,0,τq,τr]t为推进器和舵对auv施加的力与力矩，也即是输入控制量；d＝[du,0,0,0,dq,dr]t表示外界的干扰量，存在一个常数l表示干扰上界，满足0≤||d||≤l；r(η)代表的是惯性坐标系e与载体坐标系b之间的转化矩阵，其欠驱动具体形式为：

7、

8、做出以下假设：(1)auv的质心与浮心相重合；(2)忽略高于2阶的水动力阻尼；(3)忽略auv的横滚运动。基于上述假设构建出以下5自由度auv数学模型：

9、运动学模型：

10、

11、动力学模型：

12、

13、其中m表示auv的质量，表示附加质量，xu,yv,zw,mq,nr,xu|u|,yv|v|,zw|w|,mq|q|与nr|r|表示水动数,d11＝xu+xu|u||u|；d22＝yv+yv|v||v|；d33＝zw+zw|w||w|；d55＝mq+mq|q||q|；d66＝nr+nr|r||r|；w表示auv的重力,表示auv的浮力；du,dq,dr表示外部扰动分量。

14、2、步骤二：初始化auv的位置、速度信息；auv起点设为距离跟踪轨迹一段距离的任一位置，初始速度皆为0；

15、3、步骤三：基于步骤一所建立的auv数学模型，依据欠驱动auv特性建立跟踪误差模型避免非最小相位的发生；

16、定义以下位置跟踪误差：

17、η1e＝η1-η1d

18、η1为auv在惯性坐标系下的位置，其中l表示从auv质心到auv对称轴的距离，η1d＝[xd,yd,zd]t为所期望的auv跟踪位置。

19、如果将auv跟踪输出坐标设定为auv的几何中心，则η1＝[x,y,z]t，然而对于欠驱动auv而言，如果将跟踪输出设置在几何中心，可能会导致系统为非最小相位，因此对输出坐标做以下定义，来避免非最小相位的产生：

20、

21、同理定义速度误差为：

22、v1e＝v1-vc

23、其中v1＝[u,q,r]t为auv实际速度，vc＝[uc,qc,rc]t为期望速度，

24、4、步骤四：设计辅助变量，并基于此设计扰动观测器，利用反正切函数保证观测器的稳定，减少抖动，同时引入终端因子保证观测器收敛速度；

25、定义一个实际扰动与估计扰动之间的误差：

26、ed＝mv-ξ

27、其中ξ是辅助变量定义为：

28、

29、其中pd1，qd1，pd2，qd2都是正奇数，且0<pd1/qd1<1，pd2/qd2>1。λ1，λ2，λ3，λ4都是正常数且λ4>l。

30、对ed进行微分可以得到：

31、

32、之后根据计算实时ed，再根据估计扰动计算公式：

33、

34、得出估计干扰

35、5、步骤五：设计双闭环控制器，外环控制器根据位置误差产生虚拟速度控制指令，内环控制器根据实际速度和虚拟速度之间的误差产生可用控制输入，保证auv的位置与速度误差收敛至0；

36、控制器的两部分均由滑模面和趋近率构成，滑模面由终端滑模控制率引入分数阶所构成，趋近率是二阶趋近率。

37、首先定义外环控制的滑模面为：

38、

39、其中c0，c1，c2是正常数，0<β1，α0<1,β2>1，siga(x)＝|x|asign(x)。

40、定义趋近律为：

41、

42、其中进一步可以得到期望速度：

43、

44、之后根据vc设计内环控制系统得到真正的输出τ＝[τu,τq,τr]t使得v1收敛于vc，

45、所设计的滑模曲面为：

46、

47、定义趋近律为：

48、

49、进一步可以得到控制率：

50、

51、6、步骤六：在控制器中运用到auv的模型中的部分信息，扰动是未知的，这就需要将控制器与观测器相结合，观测器输出的估计扰动参与到内环控制器的计算当中，以减少内环控制器输出的执行机构的力与力矩的抖振。

52、有益效果：

53、通过定义辅助变量对干扰进行估计。对于欠驱动auv这种动力学模型高度非线性耦合、无法直接控制横荡与垂荡运动、受环境扰动影响很大的对象来说，本发明能够起到良好的控制效果，且具有较强的鲁棒性，即使在较大的动态扰动下依旧可以保持较小的误差跟踪上期望轨迹，而在观测器的帮助下可以保证控制器输出力与力矩的平稳。