一种机器人飞行系统的安全约束与降低通讯资源控制方法

本发明涉及扑翼机器人，尤其涉及一种机器人飞行系统的安全约束与降低通讯资源控制方法。

背景技术：

1、随着科技的不断进步，作为仿生学的一个重要分支，扑翼机器人理论研究和应用受到了广泛的关注。扑翼机器人通过模拟鸟类或昆虫的飞行机制，能够在空中进行高效且灵活的飞行运动。然而，由于飞行动力学的复杂性，传统控制方法往往难以实现对扑翼机器人飞行状态的精确控制。特别是在处理突发事件或需要快速响应的情况下，传统的控制方法往往无法及时做出调整，导致机器人的飞行性能下降，甚至发生飞行失稳的情况。因此，如何设计一种能够实时响应飞行环境变化，快速调整飞行策略的控制方法，成为了扑翼机器人研究领域的重要课题。

2、近年来，事件触发控制方法在机器人控制领域得到了广泛的研究与应用。该方法能够在满足一定条件时，触发控制器的动作，从而实现对机器人行为的实时调整。在扑翼机器人的飞行控制中，事件触发控制方法具有显著的优势。通过设计相应的事件触发条件，使得扑翼机器人在飞行状态发生状况时能够及时做出调整，从而保持飞行的稳定性与效率。然而，现有的事件触发控制方法在应用于扑翼机器人时，仍面临着触发条件设定复杂、控制精度不高、计算量大等问题。因此，应综合考虑触发条件、控制精度和计算量等因素，设计出更为适合扑翼机器人的事件触发控制方法。另外，在实际应用中，一旦超出控制对象的输出约束，可能会导致剧烈摩擦、高速冲击和严重挤压等危害，从而直接影响扑翼飞行器的寿命。通过合理处理系统的输出，一方面可以减少噪音、优化控制，另一方面能提高系统的鲁棒性。因此，开发一种高效且精准的事件触发约束控制方法，对于提升扑翼机器人的飞行性能具有重要意义。

技术实现思路

1、针对现有技术的不足，本发明提供一种机器人飞行系统的安全约束与降低通讯资源控制方法。

2、一种机器人飞行系统的安全约束与降低通讯资源控制方法，包括以下步骤：

3、步骤1：建立扑翼机器人飞行系统的偏微分动态系统方程，具体为：

4、

5、

6、

7、边界条件为：

8、y(0,t)＝y′(0,t)＝y″(s,t)＝θ(0,t)＝0   (3)

9、

10、

11、

12、其中，y(l,t)和θ(l,t)为柔性机翼在两个方向上的弹性变形，即弯曲变形和扭转变形；l和t为自变量；为加速度；y″″(l,t)为y(l,t)在空间上的高阶变化率，描述了机翼的高阶弯曲特性，为高阶变化率随时间的变化；y′(0,t)为在l＝0处的斜率；y″(s,t)为在l＝s处空间上的变化率；y″′(s,t)为在l＝s处曲率的变化率，为曲率的变化率随时间的变化；θ″(l,t)为角度的变化率在空间上的变化；为角速度的空间变化率随时间的变化；θ′(s,t)为在l＝s处，角度的斜率，为角度斜率的变化率。此外，fb(l,t)为沿柔性翼存在的一个时空变化的分布载荷；s为扑翼机器人的总长度；m为单位跨度的质量；ip为极惯性矩；eib为机翼的抗弯刚度；gj为机翼的扭转刚度；xec为机翼质量中心到剪切中心的距离；xac为气动中心到剪切中心的距离；η为kelvin-voigt阻尼系数；l＝s为机翼的边界；f1(t)和f2(t)分别为影响弯曲和扭转挠度的边界控制输入，fb(l,t)为沿柔性翼存在的一个分布扰动；其中，表示偏导数，和分别表示对时间t的一阶和二阶偏导数，(*)′，(*)″，(*)″′和(*)″″分别表示对l的一阶、二阶、三阶和四阶偏导数。

13、另外，由于时空变化的分布载荷fb(l,t)的能量是有界的，因此，假设fb(l,t)存在上界，即常数为正实数集，满足|fb(l,t)|≤fbmax，

14、步骤2：给出事件触发机制和机翼振动约束模型：

15、首先，给出事件触发机制如下：

16、

17、ti+1＝inf{t∈r||e1(t)|≥δ1|f1(t)|+ρ1}   (7)

18、

19、tj+1＝inf{t∈r|e2(t)|≥δ2|f2(t)|+ρ2}   (9)

20、其中，q1(ti)和q2(tj)为中间控制信号，ti和tj分别为边界控制输入f1(t)和f2(t)的更新时间；如公式(7)、公式(9)所示，当事件触发机制被激活时，触发时间为ti+1和tj+1，此时的边界控制输入f1(ti+1)和f2(tj+1)传递给执行器；e1(t)＝q1(t)-f1(t)和e2(t)＝q2(t)-f2(t)为测量误差，δ1|f1(t)|+ρ1和δ2|f2(t)|+ρ2为相对阈值，0＜δ1＜1，0＜δ2＜1，ρ1和ρ2为正设计参数，inf为下确界，r为实数；

21、在触发机制未触发时，由(7)和(9)可知，q1(t)-f1(t)≤δ1|f1(t)|+ρ1，q2(t)-f2(t)≤δ2|f2(t)|+ρ2，存在参数λi，满足|λi|≤1,i＝1,...,4，有：q1(t)＝(1+λ1(t)δ1)f1(t)+λ2(t)ρ1，q2(t)＝(1+λ3(t)δ2)f2(t)+λ4(t)ρ2，整理得：

22、给出如下的机翼振动约束模型：

23、其中，d和h分别为弯曲变形和扭转变形的约束界，y(s)和θ(s)分别为弯曲变形和扭转变形的边界，且机翼的弯曲变形和扭转变形的初始状态满足-d＜y(s,0)＜d，-h＜θ(s,0)＜h。

24、步骤3：基于扑翼机器人飞行系统的状态，根据事件触发机制设计事件触发控制器；

25、首先，选取如下lyapunov函数：

26、v(t)＝v1(t)+v2(t)+v3(t)     (10)

27、对变量l和t以及机翼总长度s进行省略，即(·)(l,t)，(·)(0,t)和(·)(s,t)分别简化为(·)，(·)，(0)和(·)(s)，有：

28、

29、

30、

31、其中，a和b是正常数。

32、创建一个新的函数：lyapunov函数v(t)有上界和下界，为：

33、

34、其中，和为正常数，η3＝max(bm+bmxec+amxec,bip+bmxec+amxec,(bm+bmxec)s4(bip+bmxec)s2)＞0；

35、对v(t)求导，得到：

36、

37、其中，σi，i＝1,2,...,7为正常数：

38、

39、

40、

41、将(16)-(18)代入(15)中，相同项系数整理，得到：

42、

43、设计控制输入q1(t)和q2(t)，即事件触发控制器：

44、

45、

46、其中，和为正常数，ε1＞0，ε2＞0。

47、由于对n为实数，ε为常数，r为实数，有-ntanh(n/ε)＜0，从事件触发控制器(20)和(21)确定因此，得到：

48、因为有j是一个实数变量，k1,k2为正常数；带入(19)中，整理后得到：

49、

50、其中，θ2＝beib-bσ3s4-bηeibσ4＞0，θ4＝bgj-bxacσ5s2-bηgjσ6＞0，σi,i＝1,...,7为正常数；

51、将(22)两边同时乘然后在[0,t]上积分，得到：

52、

53、进一步知：

54、

55、

56、对于公式(24)和(25)，当t→∞时，有：

57、

58、

59、从(26)和(27)知，由于初值有界，当t趋于无穷时y(s)和θ(s)保持在一个小的邻域内；这意味着，当t＞t时，系统状态y和θ将保持在一个小的邻域内，即和由lyapunov稳定性可知，扑翼机器人飞行系统是稳定的。

60、由于e1(t)＝q1(t)-f1(t)，和e2(t)＝q2(t)-f2(t)，从q1(t)＝(1+λ1(t)δ1)f1(t)+λ2(t)ρ1和q2(t)＝(1+λ3(t)δ2)f2(t)+λ4(t)ρ2知，和是光滑可微的函数。由于系统所有信号都是有界的，所以和也是有界的。因此，存在正常数a和b满足和由于e1(ti)＝0，e2(tj)＝0，存在正常数π1和π2，使得ti+1-ti≥π1，tj+1-tj≥π2，通过计算得到：

61、步骤4：通过matlab对步骤3中的事件触发控制输入参数和事件触发机制的阈值大小进行调节，以实现最终的控制目标。

62、采用上述技术方案所产生的有益效果在于：

63、本发明提供一种扑翼机器人飞行系统的事件触发约束控制方法，通过灵活调整事件触发控制器的参数以及事件触发机制的阈值，本发明使得扑翼机器人飞行系统在受到边界约束时，仍能有效抑制振动，同时避免了芝诺行为的发生。通过调整控制器参数及触发机制阈值确保了扑翼机器人在飞行过程中的稳定性和效率。

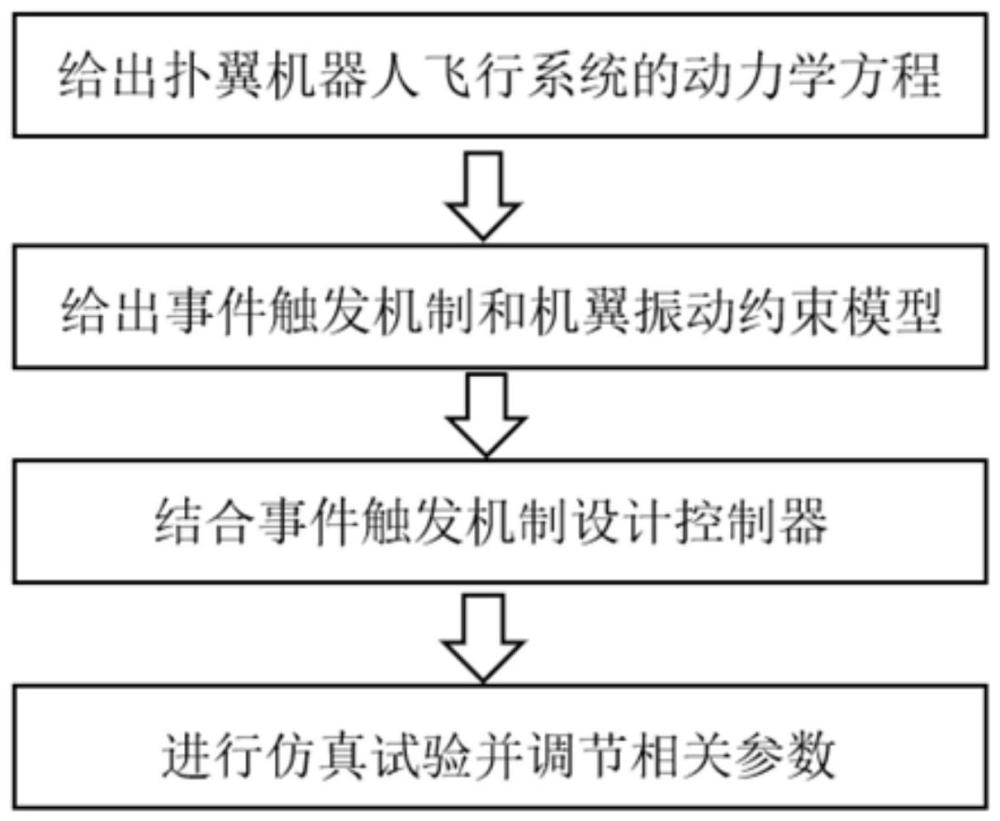
64、本发明在提高飞行效率、增强飞行稳定性与安全性以及提升自适应性和鲁棒性等方面具有显著的优势，有望为扑翼机器人在环境监测、应急搜救、军事侦察等领域的应用提供更加可靠和高效的控制策略。首先，给出扑翼机器人飞行系统的偏微分动态方程；然后，引入事件触发机制，并采用对数型函数模型对系统的输出进行约束；其次，结合事件触发机制设计控制器；最后，通过matlab进行仿真实验并调节相关参数。本发明所设计的事件触发控制器能够在存在外部干扰时，有效抑制系统的弯曲变形和扭转变形的振动，降低通信负担的同时，提高系统性能并且避免了系统的芝诺行为，对于其他扑翼机器人飞行系统的控制器设计具有一定的参考价值

65、此外，本发明将事件触发控制和输出状态约束控制融合于扑翼机器人飞行系统的控制器设计中，有效节约了通讯资源，显著提升了系统的控制效能。相较于仅依赖理想控制输入条件的传统方法，此创新方案在实际应用中更具广泛性和实用性。所提出的控制算法为扑翼机器人飞行系统提供了作业安全性和操纵稳定性保障。