基于带约束模型预测控制的无人直升机位置控制方法

本发明涉及小型无人直升机的控制，具体涉及一种基于带约束模型预测控制的无人直升机位置控制方法。

背景技术：

1、近年来，无人机由于其方便小巧，便于控制，机动性高等优势，应用于农业、军事、民用等各大领域，而且其成本低，损耗也小，在很多方面可以替代人力，使用范围十分广。

2、无人机系统具有多变量、欠驱动、强耦合、非线性等特性，所以一个高性能强大的飞行是实现无人机平稳飞行的关键。模型预测控制(mpc)是一类特殊的控制，它的当前控制动作是在每一个采样瞬间通过求解一个有限时域最优控制问题而获得。过程的当前状态作为最优控制问题的初始状态，解得的最优控制序列只实施第一个控制作用。其控制过程可以有如下简单描述：在每一采样时刻，通过测量得到状态量的值，然后在线求解开环优化问题，得到最优控制序列，通过滚动优化，将求得的控制量作用于系统。在下一采样时刻，重复上述过程。模型预测控制算法包含三个基本原理：基于模型的预测、反馈校正和滚动优化。模型预测控制能够有效地处理状态量约束问题，其可以直接把约束条件添加到算法中，显式地求解带约束条件的优化问题。另外，mpc作为一种以模型为基础的控制器设计方法，被控对象的模型可以是任意形式，只要模型可以描述被控对象的动态行为。所以mpc对线性或非线性系统、时变或非时变系统、有时延或无时延的系统的有约束最优控制问题都能进行很好的解决，成为一种适用范围广泛，实际效果良好的现代控制方法。

技术实现思路

1、本发明的目的是为了解决现有技术中的上述缺陷，根据实际的物理系统对于输入量和状态变量的限制，提供一种基于带约束模型预测控制的无人直升机位置控制方法。

2、本发明的目的可以通过采取如下技术方案达到：

3、一种基于带约束模型预测控制的无人直升机位置控制方法，所述无人直升机位置控制方法包括以下步骤：

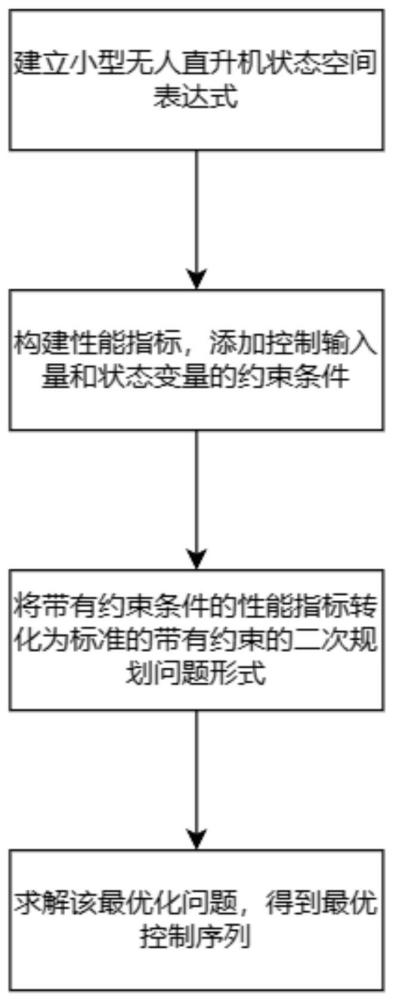
4、s1、建立小型无人直升机非线性动力学方程，并将该非线性动力学方程在平衡点附近进行线性化后转化为线性动力学方程，并进一步对线性动力学方程进行解耦得到位置控制通道，对位置控制通道离散化处理得到位置通道的状态空间方程；

5、s2、构建小型无人直升机的性能指标，添加控制输入量和状态变量的约束条件；

6、s3、将带有约束条件的性能指标转化为标准的带有约束的二次规划问题；

7、s4、求解该标准的带有约束的二次规划问题，得到小型无人直升机的最优控制序列。

8、进一步地，所述步骤s1中小型无人直升机非线性动力学方程为：

9、

10、其中u、v、w为小型无人直升机在机体坐标系下的三轴线速度，为机体坐标系下的加速度，p、q、r为绕机体坐标系三轴角速度，为机体坐标系三轴角加速度，φ为滚转角roll，θ为俯仰角pitch，ψ为偏航角yaw，fx、fy、fz为主旋翼升力在机体坐标系下的三轴分量，ixx、iyy、izz为在机体坐标系下的三轴转动惯量，l、m、n分别为滚转力矩、俯仰力矩和偏航力矩，m为直升机质量，g为重力加速度；

11、上述小型无人直升机在保持悬停的平衡状态时，对小型无人直升机线性动力学方程在平衡点附近进行线性化后转化为线性动力学方程，并进一步对线性动力学方程进行解耦得到位置控制通道，得到的状态空间方程为：

12、

13、其中x(t)表示为t时刻系统状态变量，为t时刻系统状态变量的变化量，u(t)表示为t时刻系统输入量，aa为系统控制矩阵，ba为系统输入矩阵，考虑重力加速度项和控制目标值将上述状态空间方程进行离散化处理：

14、x(k+1)＝ax(k)+bu(k)

15、其中δt为系统采样时间，x(k+1)为系统在k+1时刻的状态变量，x(k)为k时刻的状态变量，u(k)为k时刻的输入量。

16、由此得到可用于后续控制设计的一个完整的小型无人直升机的数学模型，而且在进行了线性化和控制通道的解耦操作后，可以大大简化数学模型，有助于对控制器的设计。

17、进一步地，所述步骤s2中性能指标为：

18、

19、其中np为预测控制所要求的最优化问题的预测区间，为预测区间最后时刻的系统状态，k为预测区间内各个时刻，取值范围为从0到np-1，s为末端代价权重矩阵，q为运行代价权重矩阵，r为控制输入代价权重矩阵，符号“()t”表示对括号中的元素进行转置，对状态变量和输入量添加约束条件为：

20、ul≤u(k)≤uh

21、xl≤x(k)≤xh

22、其中ul和uh为输入量的最小值和最大值，xl和xh为状态变量的最小值和最大值。

23、输入量和状态变量的最大值和最小值可以按照实际的小型无人直升机飞行状态进行给定，添加了约束条件后，可以使无人机的飞行更贴合实际的需求，并且做出适当的控制作用。

24、进一步地，所述步骤s3过程如下：

25、s3.1、把小型无人直升机预测区间np内状态变量预测值化为标准形式，预测控制中在k时刻时，小型无人直升机预测区间np内状态变量预测值表示为：

26、

27、其中x(k+1|k)，为k时刻时小型无人直升机在k+1时刻、k+2时刻、…到k+np时刻的状态变量预测值，x(k|k)为k时刻的状态变量初始值，u(k|k)，为k时刻时小型无人直升机在k时刻、k+1时刻、…到k+np-1时刻的输入值；

28、将小型无人直升机预测区间np内状态变量预测值表述为一个紧凑的形式：

29、

30、其中表示预测区间np内的状态变量，表示计算得到的控制输入量，且表示为：

31、

32、得出紧凑的状态空间方程可用于对下述的操作步骤的化简。

33、s3.2、把小型无人直升机预测区间np内性能指标化为标准形式，在k时刻时，小型无人直升机预测区间np内性能指标表示为：

34、

35、其中i取值范围从0到np-1，把初始值的代价项提取出来，此值是k时刻的初始值，不随输入变化，进一步得到性能指标为：

36、

37、组合上式中的第二、三项：

38、

39、同时用x(k)和u(k)表达便可得：

40、

41、定义

42、

43、进一步用表示：

44、

45、其中

46、s3.3、把小型无人直升机预测区间np内不等式约束条件化为标准形式，在k时刻时，小型无人直升机预测区间np内对输入量和状态变量添加的不等式约束条件化为矩阵形式：

47、mx(k+i)+nu(k+i)≤β,i＝0,1,2,…,np-1

48、

49、其中，m＝[0 0 -i i]t,n＝[-i i 0 0]t,β＝[-ul uh -xl xh]t,i为单位矩阵，利用上述的x(k)和u(k)调整该不等式约束可得：

50、

51、其中

52、

53、

54、再用u(k)来表示x(k)并简化式子可得约束条件为：

55、

56、其中在该约束条件中，x(k|k)是已知的k时刻状态变量，故只含有待求解的控制序列u(k)。

57、由此可以得到标准形式的性能指标和约束条件，这方便了最终的计算过程。

58、进一步地，所述步骤s4中，将标准形式的带约束二次规划问题表达为：

59、

60、

61、使用matlab软件中的quadprog函数求解该二次规划问题得最优解，得到最优控制序列取第一项u(k|k)作为控制量输入进去。

62、进一步地，末端代价权重矩阵s、运行代价权重矩阵q和控制输入代价权重矩阵r均是对称矩阵。而且通过调整各个矩阵的大小，可以让控制系统更加专注某部分的性能。比如，通过调整输入代价权重矩阵s可以让系统的输入更加稳定，但是会使状态变量到达稳定的时间变长，所以需要权衡实际的需求，去平衡各个矩阵的取值。

63、本发明相对于现有技术具有如下的优点及效果：

64、1、本发明针对小型无人直升机平台在实际飞行过程中所需考虑到的物理条件限制，添加了对输入量和状态变量的约束条件，使得小型无人直升机可以更加准确地跟踪给定的飞行位置。

65、2、本发明把带约束的模型预测控制问题通过离线转化为标准二次规划问题，然后在线求得最优解，在每个采样时刻根据实时反馈的初始值进行重新计算，使得在可减少计算量的同时能够及时响应系统的变化。