一种实现矩阵-向量乘法的全存内计算电路

本发明属于半导体(semiconductor)、集成电路(integrated circuit)和计算机架构(computer architecture)领域，涉及一种加速矩阵-向量乘法的全存内计算电路，具体涉及一种基于可变电阻器件(如阻变存储器、相变存储器、磁存储器、铁电存储器等)的矩阵-向量乘法计算电路设计。

背景技术：

1、矩阵-向量乘法(mvm)是众多重要算法中的核心操作，譬如科学计算、图像处理和神经网络等。在大数据时代，相关应用中的数据量急剧增长，产生了巨大的mvm计算需求。在传统的数字计算机中，mvm具有较高的计算复杂度，即o(n2)，计算速度慢、能耗大。此外，冯·诺依曼架构中存储、计算相分离的特征导致频繁的数据搬运，进一步限制了数字计算机的算力与能效。

2、基于可变电阻阵列(如阻变存储器、相变存储器、磁存储器和铁电存储器)的存内计算技术利用电路中的物理定律加速mvm计算，实现数据在存储器内部的原位计算，且提高了计算的并行度。在传统的存内计算架构中，仅矩阵元素被映射为阵列中的非易失性模拟电导值，输入向量需要连续地从片外主存(dram)中传输到片上，经由数模转换器(dac)映射为施加在阵列上的电压。对于诸如图片压缩和还原、卷积神经网络(cnn)等权重矩阵数据量较小、而输入向量数据量庞大的应用，大量的数据搬运和频繁的数模转换带来严重的计算时延与能量损耗。此外，现有的存内计算架构要求同时激活多条字线，这将增加解码器等外围电路的开销，并进一步限制了数据处理的速度和能效。因此，为了充分实现存内计算的优势，彻底消除数据搬运的开销，设计新型的存内计算架构变得必要。

技术实现思路

1、本发明的目的是基于可变电阻阵列，设计一种全存内计算电路架构，将矩阵元素和向量元素都存储在阵列中，消除数据传输、da转换和多字线同时激活带来的额外开销。

2、本发明提供的技术方案如下：

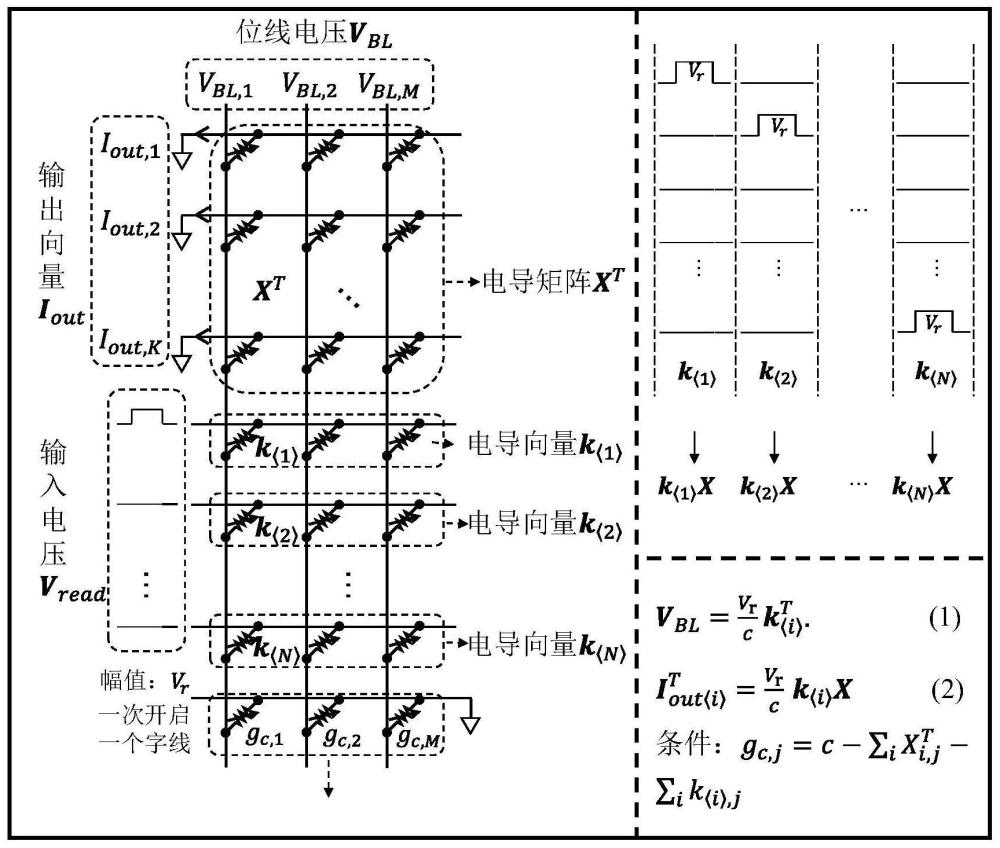
3、一种实现mvm计算的全存内计算电路，通过将mvm的矩阵和向量元素同时存储在可变电阻阵列中实现。考虑一个大小为m×k的矩阵x和n个大小为1×m的向量k<1，...，n>。该电路的核心是一个(k+n+1)×m的可变电阻阵列，其中，矩阵和向量的信息都作为模拟电导值被存储在可变电阻阵列中，它的前k行用于存储矩阵xt(矩阵x的转置)，第k+1行到k+n行用于存储n个向量，最后一行作为补偿电阻用于电导补偿。电路工作时，在阵列的第k+i行施加一个读取电压脉冲，阵列的前k行接地，其收集到的输出电流向量即为mvm的结果k＜i＞x。从k+1行到k+n行依次施加幅值、脉宽一致的读取电压脉冲循环，全部的n次mvm计算即可完成。若矩阵和向量中包含负数元素，则需要将其分成两个正数矩阵或者向量。考虑一个大小为m×k的实数域矩阵和n个1×m的实数向量，并将其表示为两个正数域矩阵或向量之差，即x＝x+-x-，k<i>＝k<i>+-k<i>-。基于一个(2k+2n+1)×m的可变电阻阵列，前2k行分别存储和两个矩阵，2k+1行到2k+2n行分别存储2n个正数域向量，最后一行仍然作为补偿电阻。电路工作时，在阵列的第2k+2i-1行和2k+2i行同时施加一组幅值相等的正负电压脉冲，则接地的前2k行收集到的电流之差即为实数域mvm的结果k<i>x。同样地，依次施加幅值、脉宽相等的正负电压脉冲，全部的n次实数域mvm计算即可完成。

4、本发明的有益效果如下：

5、本发明基于可变电阻阵列实现了一种全存内计算电路，与现有的存内计算架构相比，该电路中矩阵元素和向量元素都被存储在阵列中，因此完全避免了片外访存操作，进一步节省了数据搬运的时间和能量，且同时还避免了dram刷新的时间和能量开销。

6、本发明只需要施加幅值和脉宽固定的电压脉冲就可以完成计算，为简单的数字信号，无需施加模拟电压，因此节省了数模转换引起的额外时间和能量开销，且进一步节省了芯片的面积。

7、本发明每进行一次mvm计算仅需要激活一行(正数)或者两行(实数)字线，简化了字线译码器和其他外围电路的设计，可以进一步提高计算的速度和能效，提高集成度。

技术特征：

1.一种实现mvm计算的全存内计算电路，其特征在于，针对一个大小为m×k的矩阵x和n个大小为1×m的向量k<1，...，n>，全存内计算电路包括(k+n+1)×m的可变电阻阵列，其中，矩阵和向量的信息都作为模拟电导值被存储在可变电阻阵列中，全存内计算电路的前k行用于存储矩阵xt，即矩阵x的转置，全存内计算电路的第k+1行到k+n行用于存储n个向量，最后一行作为补偿电阻用于电导补偿，电路工作时，在阵列的第k+i行施加一个读取电压脉冲，阵列的前k行接地，所有m条列线悬空，收集到的输出电流向量即为mvm的结果k<i>x，从k+1行到k+n行依次施加幅值、脉宽一致的读取电压脉冲循环，全部的n次mvm计算即可完成。

2.如权利要求1所述的实现mvm计算的全存内计算电路，其特征在于，利用一组跨阻运算放大器将输出的电流信号转化为电压信号，用于检测以及与其他电路进行级联。

3.如权利要求1所述的实现mvm计算的全存内计算电路，其特征在于，调节补偿电阻的电导值，使得可变电阻阵列的每条列线上所有阻性器件的电导值加和等于常数c。

4.如权利要求1所述的实现mvm计算的全存内计算电路，其特征在于，若矩阵和向量中包含负数元素，将其分成两个正数矩阵或者向量，即一个大小为m×k的实数域矩阵和n个1×m的实数向量，将其表示为两个正数域矩阵或向量之差，即x＝x+-x-，k<i>＝k<i>+-k<i>-。

5.如权利要求4所述的实现mvm计算的全存内计算电路，其特征在于，全存内计算电路包括一个(2k+2n+1)×m的可变电阻阵列，前2k行分别存储和两个矩阵，2k+1行到2k+2n行分别存储2n个正数域向量，最后一行仍然作为补偿电阻，电路工作时，在阵列的第2k+2i-1行和2k+2i行同时施加一组幅值相等的正负电压脉冲，则接地的前2k行收集到的电流之差即为实数域mvm的结果k<i>x，依次施加幅值、脉宽相等的正负电压脉冲，全部的n次实数域mvm计算即可完成。

6.如权利要求1所述的实现mvm计算的全存内计算电路，其特征在于，所述可变电阻阵列中的可变电阻器件为阻变存储器、相变存储器、磁存储器或铁电存储器。

技术总结本发明提供了一种实现矩阵‑向量乘法的全存内计算电路，属于集成电路技术领域。本发明将矩阵和向量的元素同时存储在可变电阻阵列中，通过激活一行字线，施加数字信号，即可完成矩阵‑向量乘法计算。相比于之前的存内计算方法，本发明完全消除了来自主存(DRAM)的数据输入，避免了访存的时间和能量消耗，以及DRAM本身的动态功耗。此外，本发明无需数字‑模拟转换(DAC)输入，进一步节省了计算时间、功耗与芯片面积，与现有存储器体系更为兼容。本发明对于卷积神经网络(CNN)、数据压缩与还原，以及其它需要大量矩阵‑向量乘法计算的应用有着重要意义和广阔的发展前景。技术研发人员：孙仲,王识清,黄如受保护的技术使用者：北京大学技术研发日：技术公布日：2024/3/11