一种用于光学非球面元件位置误差校正的方法

本发明属于光学非球面镜片，具体涉及一种用于光学非球面元件位置误差校正的方法。

背景技术：

1、随着智能手机、安防镜头、车载镜头的性能不断提升,高精度非球面镜片的需求急剧增长,生产面形峰谷(pv)值优于0.1μm的非球面镜片逐渐成为行业主流趋势,这意味着面形检测设备只允许有几十纳米的不确定度。通过非球面面形的检测不仅可以评判光学元件的加工质量,还可以为非球面的精密加工提供反馈补偿。随着光学元件的精密化,生产高精度的非球面产品需要发展与之相适应的超精密面形检测方法与技术。

2、面形检测过程中的误差主要源于3个方面:运动轴误差、探头误差和位置偏移误差。其中,运动轴误差与探头误差往往取决于机械精度和最后补偿的精度,而位置偏移误差往往需要算法的校正。通常位置偏移误差的校正需要测量数据的不确定度在几十纳米以内,通过位置偏移误差的分离可得到真正的面形误差。

3、针对目前常用的三维校正算法，如迭代最近点(icp)算法，其在计算过程中引入了6个自由度。然而，对于轴对称的光学元件来说，绕z轴的旋转误差是无需考虑的。这种处理方式使得icp算法实际上引入了一个不必要的误差元素，导致最终计算得到的误差值与实际情况不匹配，从而影响了校正精度。相比之下，本发明采用的无约束单纯形优化策略，通过避免不必要的自由度引入，提高了误差校正的精度和效率，有效提升了算法的收敛速度和校正精度，同时显著减少了面形误差校正的计算量。这种方法针对现有三维校正算法在处理轴对称光学元件时存在的精度低和计算量大的问题，提供了一种更为高效和精确的解决方案。

技术实现思路

1、本发明的目的在于提供了一种用于光学非球面元件位置误差校正的方法，旨在解决现有技术中非球面镜片在制造和加工过程中由于机械定位、环境因素等引起的位置相关几何误差难以精确校正的问题。这种误差会严重影响镜片的光学性能和成像质量，而传统的校正方法往往计算量大、效率低下，难以满足高精度和高效率的要求。本发明的优点在于，通过结合高精度光学测量技术和先进的单纯形调优策略，能够实现对非球面镜片位置相关几何误差的快速、精确校正，显著提高校正效率、实现高精度光学性能评价。

2、本发明采用以下技术方案来实现的：

3、一种用于光学非球面元件位置误差校正的方法，包括：

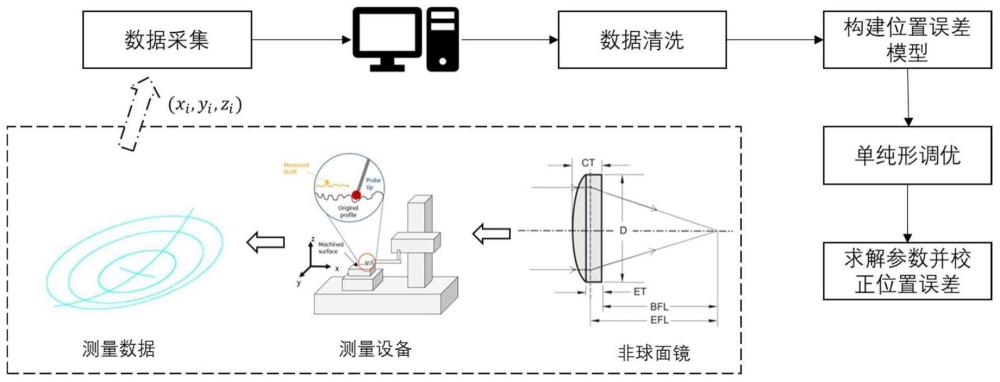
4、1)对目标非球面镜片三维坐标数据信息的收集与预处理，得到预处理的三维数据信息；

5、2)基于预处理后的三维数据信息，建立面形误差模型，并采用单纯形调优方法对面形误差模型参数执行动态优化；

6、3)利用经优化的面形误差模型定位非球面镜片的位置相关几何误差，同时计算所需的校正参数；

7、4)应用这些校正参数以对非球面镜片的位置相关几何误差进行修正。

8、本发明进一步的改进在于，步骤1)中，采用非接触式光学测量技术，对非球面镜片原始三维数据信息进行采集，以获得镜片表面形态的三维坐标数据信息。

9、本发明进一步的改进在于，非接触式光学测量技术采用激光扫描或结构光扫描。

10、本发明进一步的改进在于，对获取到的非球面三维坐标数据进行预处理，其中采用自适应滤波算法以滤除测量噪声、数据平滑技术以消除粗糙点以及异常值检测以剔除误差数据；预处理过程中，算法自动适应数据的特点，基于所测数据的统计特性调整滤波器参数，确保各项操作精确地针对三维坐标数据信息中的特异性进行。

11、本发明进一步的改进在于，步骤2)中，基于预处理后的三维数据信息，分析待测非球面在三维空间内各自由度方向的变换、建立空间综合误差模型与位置相关几何误差目标函数。

12、本发明进一步的改进在于，依据预处理后的三维数据信息，构建位置相关几何误差模型的具体步骤如下：

13、步骤2.1、在三维空间中，目标非球面镜片姿态的偏移等效于刚体在三维空间的旋转和平移，即空间中存在6个自由度的变换，分别为沿着x轴的旋转角度α，沿着y轴的旋转角度β，沿着z轴的旋转角度γ，沿着x轴的平移δx，沿着y轴的平移δy，沿着z轴的平移δz；并且，由于高次非球面沿着光轴对称，故不考虑沿着z轴的旋转角度γ；所以位置相关几何误差参数包括rx、ry、δx、δy和δz，其中rx、ry为

14、

15、

16、步骤2.2、假设测量坐标为(x0,y0,z0)，位置偏移校正后的坐标为(x1,y1,z1)，则有

17、

18、步骤2.3、假设光轴为z轴，非球面的顶点为坐标原点，非球面的方程表述为

19、

20、式中：r2＝x2+y2；e4、e6、e8为高次项系数；c为非球面的曲率半径；k为圆锥常数，当k和高次项系数为0时，曲面为球面；

21、结合非球面方程表达式，故位置相关几何误差目标函数描述为

22、f(x)＝z1-z(x1,y1)

23、式中；z(x1,y1)是将(x1,y1)代入非球面方程z求出来的值。

24、本发明进一步的改进在于，步骤3)中，根据建立的非球面位置相关几何误差目标函数，通过将实测非球面三维点云坐标数据即带有位置误差和面形误差与标准的非球面方程作对比，得到各坐标点的误差；利用均方根误差最小原理，使其误差函数值最小，迭代优化求解出相应的位置相关几何误差，得到相应的最优的位置偏移参数(α，β，δx，δy，δz)；求解最优位置偏移参数的具体步骤如下：

25、步骤3.1、位置相关几何误差目标函数f(x)为一与位置偏移参数相关的五元函数，使其误差函数值最小即等同于在多维空间寻找目标函数的最小值；根据单纯形调优法，针对多维函数f(x)，x∈rn，首先确定n+1个初始点x1、x2、…、xn+1，使其构成一个初始单纯形，对n+1个点按目标函数值进行从大到小的排序并重新命名使其满足f(x1)≤f(x1)≤…≤f(xn+1)，此时可确定函数值最大的最坏点xn+1、函数值第二大的次坏点xn和函数值最小的最好点x1；

26、步骤3.2、扣除最坏点xn+1，计算前n个点的重心并计算xn+1关于重心点m的反射点，即r＝2m-xn+1；

27、步骤3.3、反射、扩张与收缩操作：

28、若f(x1)≤f(r)<f(xn)，即反射点结果在最好点和次坏点之间，则令xn+1＝r，即去除最坏点，进入下一层循环；

29、若f(r)<f(x1)，反射点结果优于最好点，计算扩张点s＝m+2(m-xn+1)；如果f(s)<f(r)，即扩张点结果优于反射点，令xn+1＝s，并进入下一层循环，否则令xn+1＝r，此时扩张失败，进入下一层循环；

30、若f(xn)≤f(r)<f(xn+1)，即反射点结果在最坏点和次坏点之间，此时进行向外收缩，计算c1＝m+(r-m)/2；如果f(c1)<f(r)，即向外压缩点结果优于反射点，令xn+1＝c1，并进入下一循环，否则执行最后一步；

31、若f(xn+1)≤f(r)，即反射点结果比最坏点还差，此时进行向内收缩，计算c2＝m+(xn+1-m)/2；如果f(c2)<f(xn+1)，令xn+1＝c2，并进入下一层循环，否则执行最后一步；

32、若以上4个条件都不满足，则令vi＝x1+(xi-x1)/2(i＝2，...，n+1)，并且将vi赋值给xi并进入下一层循环；

33、步骤3.4、多次迭代，使得产生的单纯性能够朝着函数极小点收敛，每次迭代针对单纯形的每个点计算目标函数值，目标函数值最大的点将被另外的点代替，直到单纯形收敛到目标函数的极小点。

34、本发明进一步的改进在于，步骤3)中，对n维的位置相关几何误差目标函数f(x)对初始点的选取，保证xj-xi，(j＝2，3，...，n+1)为n个线性无关向量，否则将导致搜索过程在一个较低维的空间内进行，从而扣掉真正的极小值点；具体方法是：选取初始顶点x1，从坐标轴方向以步长h找其余n个顶点，即xj＝x1+hei，其中ei是一个单位向量，其第i个元素为1.其余元素为0。

35、本发明进一步的改进在于，步骤3)中，在进行单纯形的反射、扩张与收缩时，其变化分别由4个参数控制，分别是反射系数α>0，扩张系数β>α，收缩系数γ∈(0，1)，缩小系数δ∈(0，1)，这4个参数分别取α＝1，β＝2，

36、本发明进一步的改进在于，步骤3)中，迭代算法的停止原则取为最后的n+1个定点处的n+1个函数值的样本标准差小于预先设定的精度阈值。

37、本发明至少具有如下有益的技术效果：

38、采用高精度测量技术精确采集非球面镜片的三维数据信息，并通过数据预处理工艺增强数据的品质。在此基础上，以预处理数据为依托，构建面形误差模型，再通过单纯形调优法对模型参数进行动态、迭代的优化处理。优化后的误差模型能够精确识别非球面镜片的位置相关几何误差，并据此计算出所需的精确校正参数。这些校正参数被用于矫正非球面镜片的相关误差。本方法将高精度测量与前沿动态优化技术相结合，极大地提升了校正过程的精度与效率，同时也显著减少了计算工作量。这对于提高光学非球面元件在高精密制造及其应用领域的质量，具有显著的现实意义和应用价值。