基于全变分的耦合非负矩阵分解的图像融合方法

本发明涉及图像融合的，尤其是指一种基于全变分的耦合非负矩阵分解的图像融合方法。

背景技术：

1、高光谱图像因其丰富的光谱信息在精准农牧业、生物医药、地质灾害预测等领域都扮演着十分重要的角色。但是，由于光学传感器的局限性等众多因素，多光谱图像虽然在空间分辨率上表现出色，但其光谱分辨率相对较低；而相比之下，高光谱图像具有更高的光谱分辨率，能够捕捉更细致的光谱信息，但其空间分辨率通常较低。这极大限制了高光谱图像在许多领域的应用。因此，研究者们通常将同一场景下的高空间分辨率多光谱图像(highspatial resolution multispectral image，简称：hr-msi)和低空间分辨率高光谱图像(low spatial resolution hyperspectral image，简称：lr-hsi)进行融合，获得高空间分辨率高光谱图像(high spatial resolution hyperspectral image，简称：hrhsi)，以达到提高高光谱图像空间分辨率的目的。

2、近年来，随着越来越多的研究人员对高光谱图像融合问题产生兴趣，学术界相继提出了多种提高高光谱数据空间分辨率的方法。大致可分为如下几类：利用线性光谱解混(lsu)技术的方法、基于非负矩阵分解的方法、基于张量分解的方法和基于深度学习的方法。

3、虽然现在的融合算法表现出了良好的效果，但在某些方面仍存在一定的不足之处。如，基于张量的方法中，虽然cp分解和tucker分解展现出了卓越的图像恢复能力，并且以二者为基础的算法框架也具有良好的性能。但是这些方法并没有充分挖掘潜在因子的物理含义，从而难以利用高光谱图像中丰富的先验知识来增强融合算法的性能；基于深度学习的方法仍有两个缺点，首先这类方法需要海量数据来训练神经网络，以获得融合网络的最佳参数，其次深度卷积神经网络泛化能力较弱，在一类数据下训练得到的卷积神经网络可能并不适用于另一类型的数据。

技术实现思路

1、本发明的目的在于克服现有技术的缺点与不足，提出了一种基于全变分的耦合非负矩阵分解的图像融合方法，在保留高光谱图像空间和光谱信息的同时，显著增强了图像的细节，实现了高分辨率高光谱图像的重构。

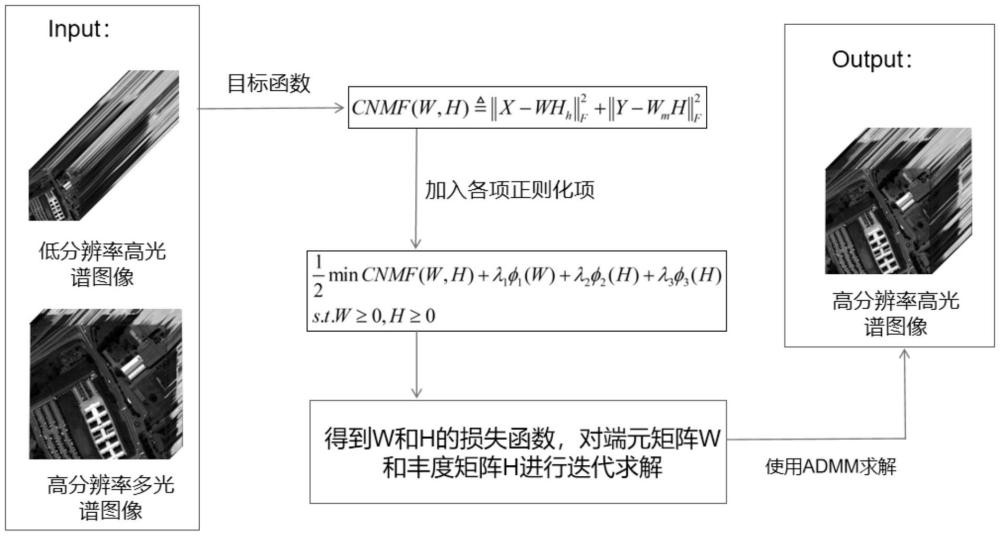
2、为实现上述目的，本发明所提供的技术方案为：基于全变分的耦合非负矩阵分解的图像融合方法，包括以下步骤：

3、s1、在二维空间内对低分辨率高光谱图像数据和高分辨率多光谱图像数据进行下采样，其中，所述高光谱图像数据是由具有非负丰度的端元光谱特征组成；

4、s2、基于耦合非负矩阵分解模型，将端元最短距离正则、丰度稀疏正则和全变分正则这三项正则化引入耦合非负矩阵分解模型中，得到联合正则化图像融合模型；

5、s3、使用交替方向乘子法admm对联合正则化图像融合模型进行优化求解，获得端元矩阵和丰度矩阵；

6、s4、将端元矩阵和丰度矩阵相乘，得到目标图像，即高分辨率高光谱图像。

7、进一步，在步骤s1中，将低分辨率高光谱图像x和高分辨率多光谱图像y看作是由目标图像z即要恢复的高分辨率高光谱图像在空间和光谱两个维度下采样得到的：

8、z＝wh+n(1)

9、x＝zs+es(2)

10、y＝rz+er             (3)

11、式中，表示实数集，p表示高光谱传感器光谱通道数，q表示高光谱图像的像素数，m表示多光谱传感器光谱通道数，n表示多光谱图像的像素数，s是空间下采样矩阵，r是光谱下采样矩阵，n、es、er分别代表残差矩阵，w是端元矩阵，h是丰度矩阵，则有：

12、x≈whh              (4)

13、y≈wmh              (5)

14、式中，hh≈hs，wm≈rw，hh表示空间下采样的丰度矩阵，wm表示光谱下采样的端元矩阵。

15、进一步，在步骤s2中，所述耦合非负矩阵分解模型的表达形式如下：

16、

17、

18、式中，表示“定义为”，||·||f表示frobenius范数，w≥0和h≥0都是非负约束，是和为1的约束，hi表示第i个端元在单个像素中的丰度分数，k是端元个数；

19、将端元最短距离正则、丰度稀疏正则和全变分正则这三项正则化添加到上述耦合非负矩阵分解模型中，得到联合正则化图像融合模型，表达形式如下：

20、

21、式中，表示端元最短距离正则项，λ1表示正则化参数，p是一个投影矩阵，λ2||h||1表示丰度稀疏正则项，λ2表示正则化参数，||·||1表示1范数；λ3||dxh||1+λ33||dyh||1表示全变分正则项，λ3表示正则化参数，dx和dy分别表示沿水平和垂直方向的二维有限差分算子，由下式给出：

22、

23、

24、进一步，在步骤s3中，使用交替方向乘子法admm对联合正则化图像融合模型进行优化求解：

25、首先，将联合正则化图像融合模型分为两个关于w和h的子问题：

26、关于w的子问题：

27、

28、式中，表示w≥0；

29、关于h的子问题：

30、

31、式中，表示h≥0；

32、然后对上述两个子问题分别进行求解：

33、对于w的子问题：引入新的变量u1，令u1＝w，则能将公式(11)转化为：

34、

35、推导出上述问题的增广拉格朗日函数l(u1,w,a1)为：

36、

37、式中，λ1＞0为正则化参数，ρ1＞0为惩罚参数，a1表示拉格朗日乘子，进一步对其优化分解，其解空间为：

38、

39、式中，wk+1表示w的第k+1次求解结果，u1k和u1k+1分别表示u1的第k次和第k+1次求解结果，a1k和a1k+1分别表示a1的第k次和第k+1次求解结果；

40、对于h的子问题：引入新的变量v1、v2、v3、v4，令v1＝h,v2＝dxh,v3＝dyh,v4＝h，则能将公式(12)转化为：

41、

42、推导出上述问题的增广拉格朗日函数为：

43、

44、式中，λ2＞0,λ3＞0为正则化参数；α1＞0,α2＞0,α3＞0,α4＞0为惩罚参数；b1,b2,b3,b4为拉格朗日乘子；使用admm算法来解决上述问题，其解空间为：

45、

46、式中，i＝1,2,3,4；hk+1表示h的第k+1次求解结果，vik和vik+1分别表示vi的第k次和第k+1次求解结果，bik和bik+1分别表示bi的第k次和第k+1次求解结果。

47、进一步，在步骤s4中，将步骤s3中优化求得的w和h使用公式(1)重构得到最终的目标图像，即高分辨率高光谱图像。

48、本发明与现有技术相比，具有如下优点与有益效果：

49、1、本发明基于经典的耦合非负矩阵分解算法，将高光谱图像和多光谱图像进行分解，建立以frobenius平方范数为代价函数的模型。但它是一个典型的病态问题，即想要得到的理想图像(高分辨率高光谱图像)可能与它的空间和光谱退化形式(可观测到的高光谱和多光谱图像)不是唯一反演的，这就使得耦合非负矩阵分解是一个不适定的逆问题。因此，为了得到更合理的解空间，对高光谱图像端元和多光谱图像丰度分别施加了最短端元距离正则化和丰度稀疏正则化来描述其稀疏性。

50、2、本发明引入了二维的各向异性的全变分正则化来描述空间和光谱域的分段平滑性，有效抑制了噪声对融合结果的影响。

51、3、通过将端元最短距离正则、丰度稀疏正则和全变分正则这三项正则化引入耦合非负矩阵分解模型中，得到了联合正则化图像融合模型，通过一系列实验表明，不管是从主观效果还是客观评价指标方面，该模型在保留高光谱图像空间和光谱信息的同时，显著增强了图像的细节，实现了高分辨率高光谱图像的重构。