一种DSOGI-PLL的LTP建模及稳定性分析方法

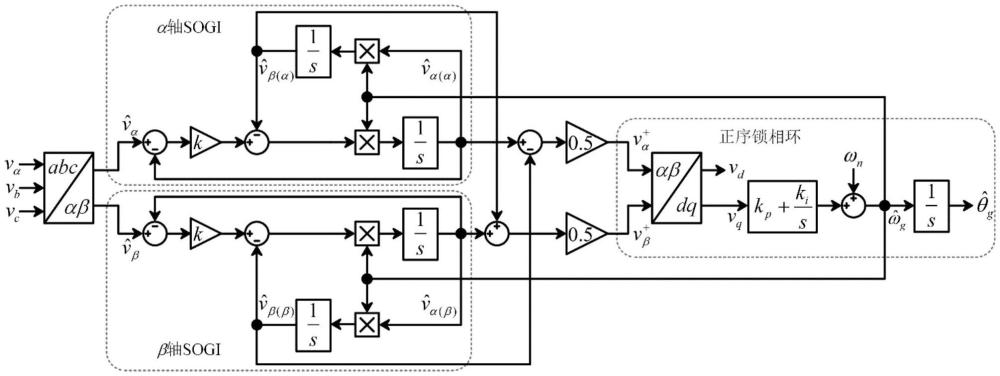
本发明涉及新能源并网同步系统稳定性评估，具体为一种dsogi-pll的ltp建模及稳定性分析方法。

背景技术：

1、基于双二阶广义积分器的三相锁相环(double second order generalizedintegrator phase-locked loop dsogi-pll)已被应用于实际电力系统的并网部分，以提高新能源发电机向电网传输的稳定性和可靠性。然而，dsogi-pll的建模和分析仍存在未知的可能性。困难在于dsogi-pll是一个非线性反馈控制系统。为解决这一问题，近年来提出了几种线性化技术来推导pll(phase-locked loop)的线性模型。现有的线性化技术大多基于线性定常(linear time-invariant lti)系统理论。在建模过程中，为了简化dsogi-pll的建模，pll的时周期动态变量被替换为标称值。应用于三相交流系统的dsogi-pll在稳态时涉及时间周期量，因此应线性化为线性时间周期(linear time period ltp)模型。然而，在lti框架下得出的线性模型忽略了dsogi-pll的周期性时变性质。随着电网中非线性负载和分布式发电系统的增加，电网受到的冲击越来越频繁，瞬态故障也越来越多，三相电网电压极易出现不平衡和畸变，锁相环的稳定工作状态也面临着巨大挑战。然而，dsogi-pll的时间周期性质并没有在三相交流系统中被建模，dsogi-pll的稳定性也没有被详细分析。为了在不平衡工况下的锁相环仍然保持稳定工作，对其进行精确建模从而获取稳定域准确范围尤为重要。

技术实现思路

1、针对上述问题，本发明的目的在于提供一种dsogi-pll的ltp建模及稳定性分析方法，以精确描述不平衡电网工况下dsogi-pll的周期时变模型以及小信号稳定性，通过准确地设计控制参数，从而保证dsogi-pll的稳定运行。技术方案如下：

2、一种dsogi-pll的ltp建模及稳定性分析方法，包括如下步骤：

3、步骤1：根据三相交流系统中的公共耦合点处三相电网电压信号，得到其在两相静止坐标系下的α、β轴电压分量，及各自的正交信号；结合三相dsogi-pll拓扑结构，推导时域下的控制微分方程，利用小信号线性化的方法，保留多频耦合关系项，建立精确的ltp模型；

4、步骤2：将建立的ltp模型表示为无穷维的lti模型，推导出三相dsogi-pll的开环谐波传递函数；

5、步骤3：基于s2步骤中建立的开环谐波传递函数，利用广义奈奎斯特稳定判据分析多变量lti反馈控制系统，并分析得到小信号稳定区域边界。

6、更进一步的，所述步骤1中得到其在两相静止坐标系下的α、β轴电压分量，及各自的正交信号具体为：

7、将三相交流系统中的公共耦合点处三相电网电压信号va、vb、vc经clark变换，得到两相静止坐标系下电网电压信号的α、β轴分量vα、vβ，分别经过二阶广义积分器处理得到电网电压信号的α轴分量vα的正交信号和以及β轴分量vβ的正交信号和相关方程如下：

8、

9、其中，vx(t)和vβ(t)为vx的时域表示；vx和θx分别为vx(t)的额定幅值和额定相位，且分别为θx＝∫ωdt，ω为系统角频率；为估计幅值，为估计相位；下标x表示α轴或β轴。

10、更进一步的，所述步骤1中，推导时域下的控制微分方程具体为：

11、将电网电压信号的α、β轴分量vα、vβ的正交信号通过合成得到正序分量和经park变换得到两相旋转坐标系下的电压，用于正序锁相环的输入信号，再经过锁相环后产生相位同步信号，用于电网同步；相关方程如下：

12、

13、其中，kp、ki分别为正序锁相环比例积分控制器的比例系数和积分系数，k为sogi阻尼系数；为电网估计角频率，为电网估计相位，ωn为电网额定频率；当dsogi-pll以准静态运行时，有下标x表示α轴或β轴。

14、更进一步的，所述步骤1中，建立精确的ltp模型具体为：

15、定义具有微小扰动的实际变量和估计变量，并将式(2)小信号线性化得到所述dsogi-pll的小信号模型，进而得到一个针对dsogi-pll的ltp模型；

16、dsogi-pll的小信号模型如下：

17、

18、其中，δ和下标n分别表示小扰动和额定值；θn为额定相位，δve(x)为幅值扰动，δθe(x)为相位扰动；为电网角频率扰动，为α轴下sogi输出相位扰动，为β轴下sogi输出相位扰动；且

19、更进一步的，步骤s2中推导出三相dsogi-pll的开环谐波传递函数，具体为：

20、根据得到的dsogi-pll的小信号模型，将输出信号和经过拉普拉斯变换；再定义ωp＝2ωn，ωp为二倍额定频率；并根据欧拉公式得到三相dsogi-pll的开环谐波传递函数：

21、

22、其中，为幅值扰动估计值的频域表示；为相位扰动估计值的频域表示；λ为前向通道增益，且表示拉普拉斯变换；gpi(s)表示pi控制器传递函数，且

23、更进一步的，通过将sm替换s，并用矩阵描述所提出的ltp模型，得到如下式的开环htfg(s)，从而用lti模型表示dsogi-pll的ltp动态；

24、y＝kg(s)e                             (5)

25、其中，y为输出量，k为前向通道增益，g(s)为系统开环谐波传递函数，e为输入误差；具体表达式如下：

26、

27、

28、

29、

30、其中，m(s)＝(0.5gpi(s)+1)i(s)，n(s)＝0.5gpi(s)i(s)；s0、s-1和s+1分别表示基本频率分量、负序频率分量和正序频率分量。

31、更进一步的，所述步骤3具体为：确定dsogi-pll在不同电网工况下各个控制参数的稳定区域，保证dsogi-pll保持电网同步稳定；通过广义奈奎斯特准则对式(5)中表示的多输入多输出(multiple input multiple output mimo)系统进行稳定性分析，对于ltp模型构成的反馈控制系统，假设表示属于由-jωp/2≤im(s)≤jωp/2区间的htfg(s)的特征值，λi(s)为g(s)的特征值，im(s)为系统奈奎斯特图虚轴；用n表示开环谐波传递函数的右半侧极数，当且仅当开环谐波传递函数的特征值沿逆时针方向恰好围绕-1/k(式(5)中的k)点恰好n次时；闭环ltp系统渐近稳定。

32、本发明的有益效果是：

33、1)本发明所提出的ltp模型可以准确地描述三相dsogi-pll的周期性时变性质。

34、2)本发明采用ltp方法，提出了一种精确的参数设计方法。

35、3)本发明利用所提出的ltp模型，可以有效地预测dsogi-pll的稳定区域。