一种融合储能的光伏发电系统并网逆变器的建模与稳定性分析方法

本发明涉及本发明涉及一种融合储能的光伏发电系统并网逆变器的建模与稳定性分析方法，属于新能源系统稳定性分析领域。

背景技术：

1、新能源发电具有波动性的特点，风电、光伏等新能源大规模集中并网对电网的规划、运行都将提出新的挑战。为平抑新能源的功率波动，储能技术受到了越来越多的重视。根据电能转换方式的不同，储能技术分为机械、电磁和化学储能三大类，其中电池储能系统(battery energy storage system，bess)具有动态吸收能量并适时释放的特点，可以平滑风能、太阳能等新能源输出功率的波动性，是间歇性可再生能源发电设备必要的补充。同时，新能源系统的并网会导致大量的电力电子装置接入电网，使电力系统面临着设计复杂、系统稳定运行分析困难等问题。

2、在储能结合光伏发电系统这一应用场景下，需要建立光储融合系统模型来分析储能对光伏系统的影响。陆秋瑜等的多时间尺度的电池储能系统建模及分析应用建立了基于戴维南等效电路的储能系统模型，通过多时间尺度的储能系统仿真模型验证了所建立的储能系统模型具有良好的适用性；蔡国伟等的风光储联合发电系统的建模及并网控制策略针对间歇性能源并网出力波动的问题，提出一种有效抑制功率波动的风光储融合发电模型，并采用外环功率与内环电流控制策略，通过仿真验证说明所提风光储融合发电模型及控制策略可有效地抑制风光系统功率波动；任勇等的独立光储直流微网的稳定运行控制策略以及刘海涛等的考虑功率限值管理的光储系统建模及控制策略中为提升光储混合的稳定运行，均提出了mppt与其他方法进行统一，通过实验验证该控制方法额能够改善系统的控制性能提升能量利用效率；徐玉琴等的基于稳压控制的独立光储微电网控制策略研究及仿真分析基于独立光储系统，提出基于稳压控制的控制策略，通过仿真验证所提控制策略能够维持光储系统稳定输出；叶小晖等的电池储能系统的多时间尺度仿真建模研究及大规模并网特性分析为研究储能电池对电网的影响，提出了一种电池储能系统的多时间尺度仿真模型，通过仿真验证得出储能系统对电网稳定性有改善作用且能够抑制新能源发电系统的功率波动；储能系统应用于新能源系统，能够有效的抑制新能源系统的出力波动并且能够提升系统的电能质量。

3、光储融合系统进行并网，逆变器起着关键的作用，而电力电子装置的接入会影响系统的暂态稳定性。熊家祚等的大规模电力电子设备接入的电力系统混合仿真接口技术综述阐述了当大量电力电子设备接入后，采用机电暂态与电磁暂态结合的混合仿真能够提升对系统的分析能力；陈磊等的电力电子接口新能源并网的暂态电压稳定机理研究基于微分代数系统稳定性分析了新能源发电系统暂态稳定问题，暂态过程中系统发生暂态电压失稳时新能源发电系统的功率平衡方程无解，通过仿真验证得出系统失稳时存在由同步机的功角失稳变为风电主导的电压失稳的情况；朱蜀等的电力电子化电力系统暂态稳定性分析综述将电力电子化电力系统的暂态稳定性分析划分为三个层次，研究了电力电子化电力系统与传统电力系统的暂态稳定性分析差异，提出了分析电力电子化电力系统暂态稳定性的方法；胡家兵等的电力电子并网装备多尺度切换控制与电力电子化电力系统多尺度暂态问题分析了电力电子变换装备暂态特性以及电力电子化电力系统暂态过程特征的基本认识，总结了电力电子化电力系统多尺度非线性暂态问题分析的基本挑战与初步研究思路。逆变器的建模是电力电子化系统稳定性分析工作的关键，其根据电网结构可构建具有l型滤波器或考虑电网阻抗的三相模型，也可构建低阶数的逆变器小信号模型，从而分析系统参数对稳定性的影响以及系统的小信号稳定；为了分析系统的暂态稳定，采用等面积法则可分析在大扰动下逆变器的稳定性，或是分析逆变器的暂态功角稳定。但是在电力电子化的系统中，电力电子器件的模型往往呈现出高阶性，模型降阶有助于简化问题的求解过程，提高计算效率。其中，采用奇异摄动降阶法能够将高阶微分方程系统降阶为更简单的形式避免直接求解高阶微分方程而导致计算复杂度的增加；在分析电力电子化系统的稳定性时，能量函数法能够直观的评估系统稳定性，通常采用变量梯度法、克拉索夫斯基法和线性矩阵不等式法构造能量函数，其中变量梯度法适用于线性和非线性系统，具有灵活性和高效的收敛性，可快速确定系统的稳定点；当光储联合系统并网时，通常采用下垂控制来调节有功与无功的控制系数，进而调整电网的电压和频率以平衡各系统的出力，满足电网稳定运行的需求。

4、目前，新能源系统的出力具有较强的不确定性，其并网后会影响系统的稳定运行状态，储能系统的应用能够抑制新能源系统出力的波动，但是储能系统和新能源系统的应用会导致大量电力电子装置并入电网，电网的拓扑结构随着电力电子器件的动作而变得非线性程度强、结构复杂，同时导致系统模型状态方程阶数更高，这些特点给光储融合并网后系统的稳定性分析带来了挑战。针对以上问题，首先，采用基于下垂控制的逆变器模型，分析了储能对新能源出力的支撑与波动抑制的能力，基于此模型构建了其状态空间方程；其次，采用奇异摄动法对逆变器状态空间方程进行降阶处理，简化稳定性分计算过程；最后，基于逆变器的低阶状态空间方程采用克拉索夫斯基法、线性矩阵不等式方法和变量梯度法三种方法构建了其李雅普诺夫函数分析储能接入后对光伏系统功角稳定的影响，求解在不同的运行状态下系统的功角稳定域。

技术实现思路

1、本发明提供了一种融合储能的光伏发电系统并网逆变器的建模与稳定性分析方法，以用于解决大量的大量电力电子器件接入电力系统后，导致其暂态行为改变且拓扑结构状态变量阶数变高使得对系统进行稳定性分析困难的问题。

2、本发明的技术方案是：一种融合储能的光伏发电系统并网逆变器的建模与稳定性分析方法，所述方法的具体步骤如下：

3、step1、基于融合储能的光伏系统构建采用下垂控制的并网逆变器模型及其状态空间方程；

4、step2、采用奇异摄动法对逆变器状态空间方程进行降阶处理；

5、step3、根据逆变器的低阶状态空间方程采用克拉索夫斯基法、线性矩阵不等式方法或变量梯度法三种方法构建光伏系统李雅普诺夫函数，利用构建好的光伏系统李雅普诺夫函数进行稳定性分析。

6、作为本发明的进一步方案，所述step1的具体步骤是：

7、step1.1、在光伏系统中，光伏系统的输出功率表示为式(1)所示：

8、

9、式中：ppv为光伏系统输出的有功功率，qpv为光伏系统输出的无功功率，ugd、ugq和id、iq分别为光伏系统并网点的电压和电流d-q轴分量；

10、若式(1)中存在电网电压与ugd相同的情况，则式(1)中ugq为0，此时可将式(1)转换为

11、step1.2、为了将储能与光伏发电模型进行联立，储能电池模型等效为：

12、

13、式中：ssoc为电池的储能容量，qn为电池储能的额定值，pes为储能电池的功率输出，s0为soc初始值；

14、将储能电池模型转换为功率模型：

15、pes＝qn(s0-ssoc)                        (4)

16、step1.3、光伏发电系统向逆变器传输的有功功率和无功功率如式(2)所示，储能系统向逆变器传输的功率如式(4)所示，光伏发电系统、储能系统和逆变器三者之间的能量传输关系如式(5)所示：

17、pinv＝ppv+pes                          (5)

18、式中：pinv为逆变器输出功率；

19、逆变器需采用合理的控制方式对光储系统输出功率进行灵活调节，以提升新能源发电系统并网后电网的稳定性，基于下垂控制的逆变器动态数学模型如式(6)所示：

20、

21、式中：δ为逆变器虚拟功角；ω、ω0、ωl分别为逆变器输出端口的角频率、电网角频率和滤波器角频率；p、q分别为逆变器输出的有功功率和无功功率；e、u、um分别为逆变器的输出电压、电网电压和参考电压幅值；xs为线路的等效电抗；ps、qs分别为有功功率和无功功率设定值；kp、kq为有功和无功的下垂控制系数；

22、并网逆变器系统的参数如下：电网频率为50hz，工频电压为5773.5v，ps、qs分别为50kw和0var，有功下垂系数kp、与无功下垂系数kq为1e-4，滤波电感为0.4mh，滤波电容为0.5mf，截止频率为355hz，将式(6)改写为式(7)所示：

23、

24、式中：将系统的状态变量表示为x，x＝[x1，x2，x3]t＝[δ，ω，e]，经过求解得到系统的平衡点为x0＝[0.000046，314.16，24989.39]；

25、将公式(7)由平衡点向原点平移得到如式(8)所示的状态空间方程：

26、

27、式中：系统由平衡点向原点平移后的状态变量由z进行表示，z＝[z1，z2，z3]t＝[δ+δ0，ω+ωg，e+e0]t，其中δ0，ωg，e0为系统平衡出的逆变器虚拟功角、电网角频率、逆变器的输出电压。

28、作为本发明的进一步方案，所述step2的具体步骤是：

29、step2.1、采用奇异摄动法对逆变器状态空间方程进行降阶处理，将逆变器状态空间方程描述为式(9)：

30、

31、式中：x、y、z为系统状态变量；

32、step2.2、引入变量ε作为缩放参数，该参数用于衡量系统中快速和慢速变化之间的差异，并定义新的时间变量τ＝εt用于描述系统的快慢速变化，将系统分解为快速和慢速变化两部分，其表达式为式(10)所示：

33、

34、式中：x0，y0和z0是慢变化部分；x1，y1和z1是快速变化部分；x2，y2和z2是更高阶的快速变化部分；

35、

36、

37、式中：x1(0)、x2(0)、x3(0)为系统慢变化部分，x1(1)、x2(1)、x3(1)为系统快变化部分；

38、通过摄动展开后求解快速变量的表达式并带入慢速变化方程中消除快速变量得到二阶的系统状态方程；采用奇异摄动法对式(8)降阶后为：

39、

40、将式(13)化简为：

41、

42、作为本发明的进一步方案，所述step3中包括：

43、采用克拉索夫斯基法构建系统李雅普诺夫函数时，将系统描述为式(15)所示：

44、

45、式中：x为系统状态变量，对所有t∈[0,∞]有f(0)＝0，即状态空间原点x＝0为系统孤立平衡状态；x＝[x1，x2，…，xn]t，f(x)＝[f1(x)，f2(x)，…，fn(x)]t，进而确定出系统的雅可比矩阵为式(16)：

46、

47、在构建系统的李雅普诺夫函数时需要验证ft(x)+f(x)＜0即负定，既有dv(x)/dt＜0即负定；

48、

49、当式(17)为负定时，系统的李雅普诺夫函数定义为式(18)：

50、v(x)＝ft(x)f(x)     (18)。

51、作为本发明的进一步方案，所述step3中包括：

52、采用线性矩阵不等式方法构建系统李雅普诺夫函数时将系统状态方程表示为式(19)：

53、

54、式中：x为系统状态变量，a为系统矩阵，选择一个对称正定矩阵p作为李雅普诺夫矩阵，并根据李亚普诺夫函数定义构造线性不等式矩阵如式(20)所示：

55、atp+pa＜0      (20)

56、由此求解出矩阵p，并构建系统李雅普诺夫函数如式(21)所示：

57、v(x)＝xtpx     (21)。

58、作为本发明的进一步方案，所述step3中包括：

59、采用变量梯度法进行构造系统李雅普诺夫函数时，其中变量梯度δv(x)为：

60、

61、式中：x为系统状态变量；

62、

63、一个连续的向量函数v′为一数量函数的梯度的充要条件为式(24)所示的雅可比矩阵m：

64、

65、若雅可比矩阵m为对称矩阵，则：

66、

67、式中：aij为待定的系数；

68、根据稳定性的需求对梯度进行约束，表示为：

69、

70、利用势场的理论可得：

71、

72、将式(25)与式(27)结合求解出变量梯度法中的系数矩阵，根据求解出的梯度δv(x)进行李雅普诺夫函数构造可得式(28)：

73、

74、将式(28)简化推出式(29)：

75、

76、采用克拉索夫斯基法求解的系统李雅普诺夫函数如式(30)所示：

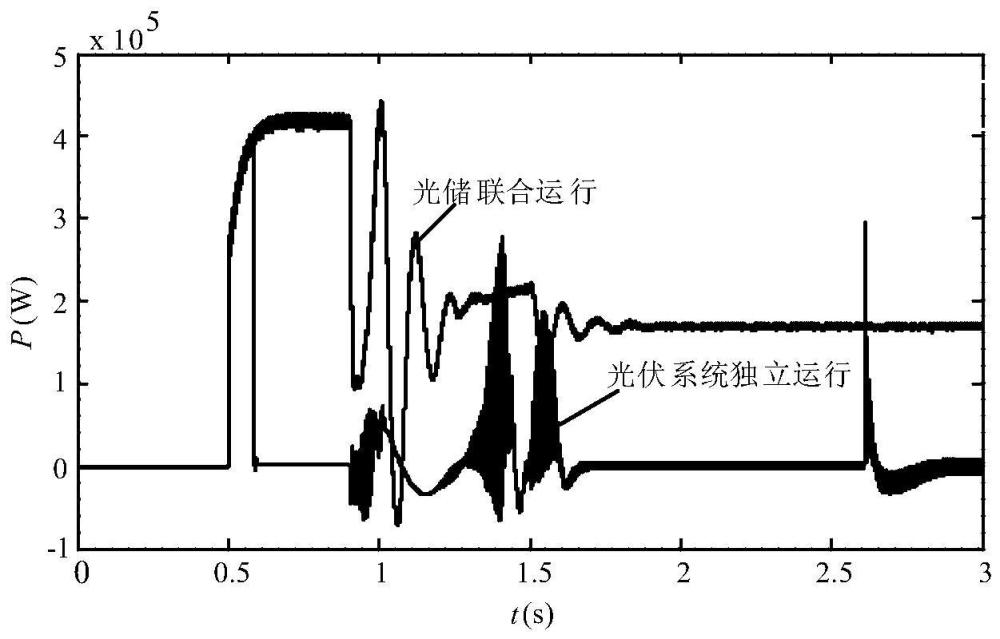
77、

78、采用线性矩阵不等式法构造的李雅普诺夫函数如式(31)所示：

79、v(z)＝δ2(z1+z2+2z1z2)     (31)

80、采用变量梯度法构造的李雅普诺夫函数如式(32)所示：

81、

82、为保持系统稳定运行，李雅普诺夫函数需满足式(33)和式(34)所示的约束条件，表示李雅普诺夫函数的导数；

83、v(z)≥0     (33)

84、

85、本发明的有益效果是：

86、(1)采用本发明所提方法可在光伏发电系统在低渗透率的状态下，储能系统接入后提升新能源系统出力的能力；

87、(2)光伏发电系统融合储能系统后，储能系统抑制新能源发电系统出力波动的能力；

88、(3)在三种李雅普诺夫函数建模方法下储能系统的接入对系统稳定性的影响，对比接入和未接入储能系统两种状态下对系统功角变化，分析储能系统对系统功角的影响。此外，在采用变量梯度法构造的系统李雅普诺夫函数能够有效求解系统的功角稳定域。