基于傅里叶级数区域分解的芯片热分析方法及系统

本发明涉及芯片分析领域，具体涉及基于傅里叶级数区域分解的芯片热分析方法及系统。

背景技术：

1、随着芯片尺寸不断缩小，功率密度不断增大，电路所消耗的电能部分转化为热能，导致芯片内的温度升高，电路可靠性降低。在芯片中安装温度传感器或使用热成像技术测量芯片热分布的方法在空间上面临诸多挑战，故一种在芯片设计初期就能准确预测芯片热分布的技术被提出，可以根据预测结果对芯片设计不断优化。

2、芯片的热分析分为数值方法和模拟方法两类。数值方法采用有限差分法或者有限元方法将热方程转化为rc网络方程进行求解，该过程中需要对整个芯片进行网格划分，网格划分的精细程度决定了热分析的精确度，例如公布号为cn117218316a的现有发明专利申请文献《基于先进工艺下芯片封装结构的热分析网格空间划分方法》，该现有方法根据芯片封装结构的物理模型，进行结构轮廓提取，采用网格生成算法生成底纹网格、贯通网格和树状网格，底纹网格用于满足基本的网格密度需求以及描述封装结构的轮廓，贯通网格用于描述结构内部复杂热源以及边界条件的轮廓，树状网格用于对热源及其周边进行自适应的加密；通过这三类网格的组合实现对于封装内部的复杂结构与复杂热源分布的自适应，以及公布号为cn105718638a的现有发明专利申请文献《一种芯片三维热分析方法》，该现有方法包括以下步骤：s1、获取芯片数据，并根据一般随机算法生成转移区域表；s2、根据芯片数据，计算用于一般随机行走时所需的转移概率；s3、输入热源区域内待计算温度点的坐标，并结合基于混合随机行走算法的芯片热分析模型中对应的区域，根据转移概率进行一般随机行走方法的温度计算，根据转移区域表进行悬浮随机行走方法的温度计算；s4、完成该坐标的温度计算后，返回步骤s3，进行下一个待计算温度点的温度计算，直到完成所有输入坐标点的温度计算。此外，许多基于数值方法的研究致力于减少其计算时间，这种方法具有灵活处理复杂结构的能力，主要应用于后端设计阶段如后期的布局时的温度分析。芯片设计早期的热分析，需要在较小的计算量下给出合理准确的温度预测。解析方法可以避免对整个芯片衬底进行网络划分，灵活的获取指定区域的温度分布。例如基于green函数的解析方法，极大的提升了芯片热分析的速度。尽管如此，上述技术存在以下缺陷：

3、第一，有限元法虽然提供了很高的精度，但由于需要对整个芯片衬底进行网格划分，所以计算量极大，计算时间长。

4、第二，green函数等传统解析方法计算速度有着显著提高，但芯片的格林函数本身非常复杂。

5、综上，现有技术存在热分析速率及精度较低，以及温度求解效率较低的技术问题。

技术实现思路

1、本发明所要解决的技术问题在于：如何解决现有技术中热分析速率及精度较低，以及温度求解效率较低的技术问题。

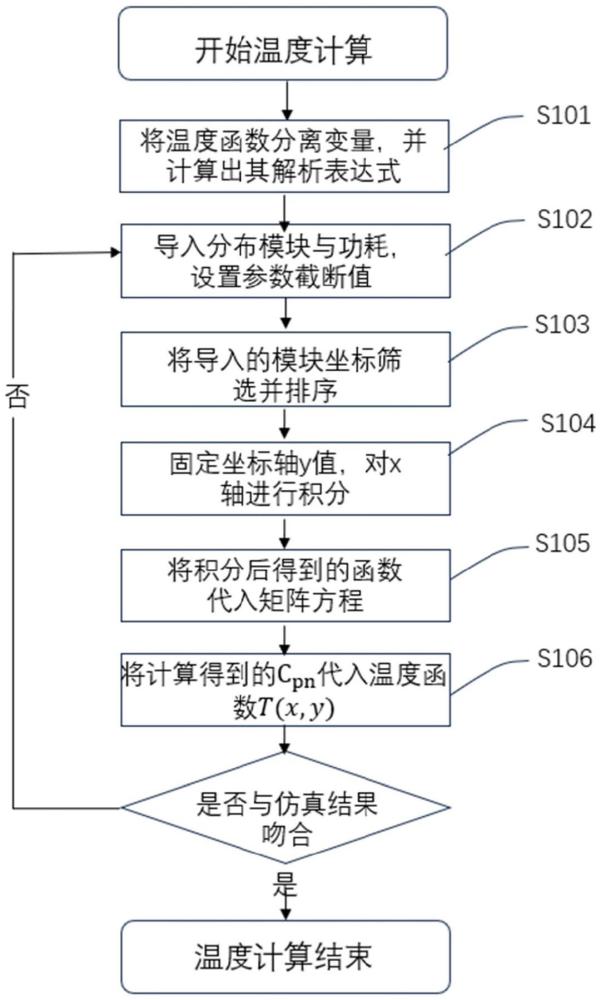
2、本发明是采用以下技术方案解决上述技术问题的：基于傅里叶级数区域分解的芯片热分析方法包括：

3、s1、获得芯片区域分布数据集，功耗分布数据集以及验证数据集；

4、s2、根据芯片区域数据集将预置面积的矩形芯片划分为不少于2个芯片区域，处理得到各个芯片区域的位置坐标、功耗，据以处理得到芯片温度分布，利用分离变量的方法展开并转换得到非齐次微分方程，以转换得到并求解齐次微分方程，求解齐次方程，得到解un(y)，据以处理得到芯片各区域温度；

5、s3、将解un(y)带入预置表达式中进行循环操作，以完成函数值遍历、累加操作，得到温度分布结果t(x,y)；

6、s4、将温度分布结果t(x,y)与有限元仿真结果进行比较，判断温度分布结果t(x,y)的精确度，对数值积分方法和解析方法进行对比，获取算法运行精度速度判定结果。

7、本发明采用解析方法，通过变量代换计算并实现偏微分传热方程的理论上通解，加速了热分析的速率。

8、在更具体的技术方案中，步骤s2包括：

9、s21、根据芯片区域数据集将预置面积的矩形芯片划分为不少于2个芯片区域，处理得到各个芯片区域的位置坐标、功耗；

10、s22、设定功耗与温度关系方程、边界条件，据以处理得到芯片温度分布；

11、s23、将f(x,y)用分离变量的方法展开并带入功耗与温度关系方程，以转换得到非齐次微分方程；

12、s24、对非齐次微分方程进行变量代换操作，得到齐次微分方程，求解齐次方程，得到解un(y)；

13、s25、设函数fn(y)有num_seg_f段，据以获取num_seg_f组不同的边界系数c1，c2，得到2*(num_seg_f-1)个边界条件；

14、s26、根据2*(num_seg_f-1)个边界条件，对应的num_seg_f组不同的常系数c1，c2，设置方程组系数矩阵a，边界系数矩阵c，据以构建得到矩阵方程组；

15、s27、求解矩阵方程组，得到解un(y)，据以处理得到泛定方程。

16、本发明采用解析方法，通过变量代换求出偏微分传热方程的理论上通解，再将这种通解用代码的实现，极大的加速了热分析的速率。

17、在更具体的技术方案中，步骤s24中，利用下述逻辑，将不同芯片区域中的边界参数带入预置函数关系，求解得到un(y)以及函数fn(y)。

18、在更具体的技术方案中，利用下述逻辑，求解得到un(y)以及函数fn(y)：

19、

20、

21、在更具体的技术方案中，步骤s25包括：

22、s251、代入不同的边界条件，在函数fn(y)的每一个分界点，得到分界点参数关系；

23、s252、根据2*(num_seg_f-1)个边界条件，在边界上确定边界参数关系；

24、在更具体的技术方案中，步骤s251中，利用下述逻辑，表达分界点参数关系：

25、un(y-)＝un(y+)

26、

27、在更具体的技术方案中，步骤s252中，利用下述逻辑，表达边界参数关系：

28、

29、

30、在更具体的技术方案中，步骤s26中，利用下述逻辑表达矩阵方程组：

31、ac＝b。

32、在更具体的技术方案中，步骤s27中，利用下述逻辑表达泛定方程：

33、

34、在更具体的技术方案中，基于傅里叶级数区域分解的芯片热分析系统包括：

35、数据模块，用以获得芯片区域分布数据集，功耗分布数据集以及验证数据集；

36、温度求解模块，用以根据芯片区域数据集将预置面积的矩形芯片划分为不少于2个芯片区域，处理得到各个芯片区域的位置坐标、功耗，据以处理得到芯片温度分布，利用分离变量的方法展开并转换得到非齐次微分方程，以转换得到并求解齐次微分方程，求解齐次方程，得到解un(y)，据以处理得到芯片各区域温度，温度求解模块与数据模块连接；

37、温度分布处理模块，用以将解un(y)带入预置表达式中进行循环操作，以完成函数值遍历、累加操作，得到温度分布结果t(x,y)，温度分布处理模块与温度求解模块连接；

38、算法判定模块，用以将温度分布结果t(x,y)与有限元仿真结果进行比较，判断温度分布结果t(x,y)的精确度，对数值积分方法和分段解析方法进行对比，获取算法运行精度速度判定结果，算法判定模块与温度分布处理模块连接。

39、本发明相比现有技术具有以下优点：

40、本发明采用解析方法，通过变量代换计算并实现偏微分传热方程的理论上通解，加速了热分析的速率。

41、本发明采用解析方法，通过变量代换求出偏微分传热方程的理论上通解，再将这种通解用代码的实现，极大的加速了热分析的速率。

42、本发明解决了现有技术中存在的热分析速率及精度较低，以及温度求解效率较低的技术问题。