基于时变谐波能量结构的高胡乐音音域拓展方法

本发明涉及音频处理，特别涉及一种基于时变谐波能量结构的高胡乐音音域拓展方法。

背景技术：

1、在数字域上研究高胡的音域拓展方法，补全胡琴乐器的中低音声部，具有重要的研究意义。

2、数字域上的高胡的音域拓展的关键是要保证生成的低音音频表现出来的乐器音色要与胡琴音色相似，而简单通过重采样将高音音频转为低音音频是无法达到这个效果的。但同时，现实缺少可供参考的胡琴低音音色，需要借助参考其他乐器的高低音频的音色关系来进行音域拓展。其中，西方的提琴乐器家族，按照音域分布高低排序分别是小提琴、中提琴、大提琴、低音提琴，这四种乐器包含高、中、低声部，音域极为宽广，因此它们包揽了西方交响乐演奏乐器的弦乐组。提琴乐器音色风格多元，具有极强的亲和力，因其在音色表达上的突出优势，它们始终占据交响乐的主导地位。同时，提琴乐器与胡琴乐器同为拉弦乐器，在发声原理与演奏手法上有共同之处，因此，参考提琴乐器之间的音色关系，对胡琴乐器进行音域拓展具有价值和可行性。

3、目前的音域拓展大多是需要对源乐音和目标乐音数据进行模型训练，这种模型通常需要大量的音频数据进行训练，而且需要花费大量的时间和计算资源。

技术实现思路

1、本发明的目的是为了解决现有技术中的上述缺陷，提供了一种基于时变谐波能量结构的高胡乐音音域拓展方法。基于时变谐波能量结构的高胡音域拓展基于传统音频处理算法，具有计算复杂度低且高效的优点，且能保持胡琴音色进行音域拓展，对解决民乐交响化具有重要意义。

2、本发明的目的可以通过采取如下技术方案达到：

3、包括以下步骤：

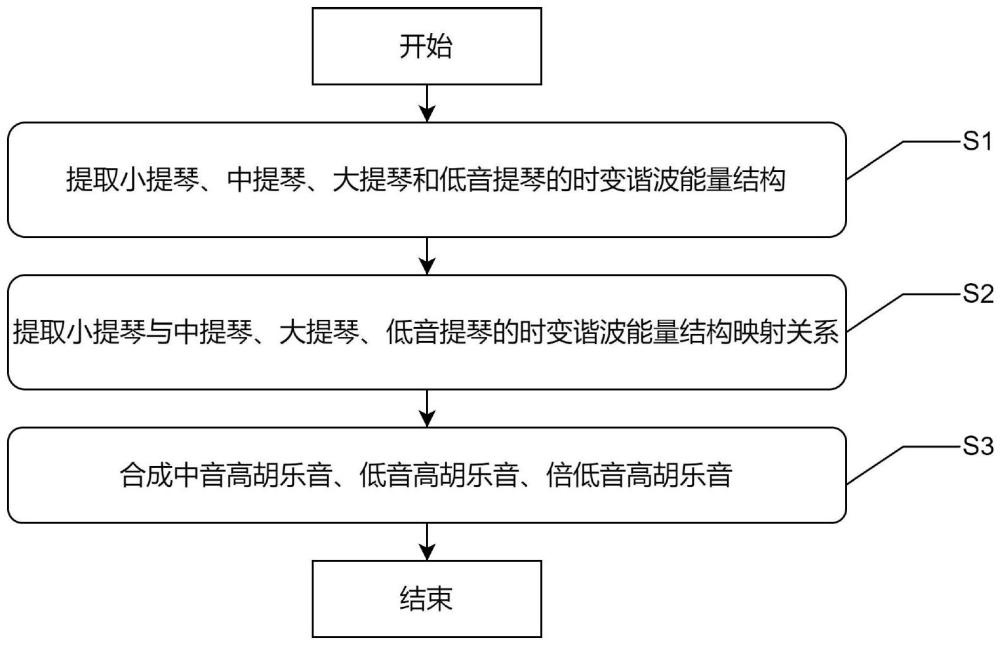
4、s1、使用自适应频谱分辨率的短时傅里叶变换得到提琴乐音样本的每一帧的频谱；自适应窗口的谐波能量结构提取方法得到提琴乐音的时变谐波能量结构；

5、s2、归一化提琴乐音样本的时变谐波能量结构；线性插值对齐多个提琴乐音样本的时变谐波能量结构；使用基于向量距离的加权平均提取多个源提琴乐音样本的能量质心和多个目标提琴乐音样本的能量质心；计算源提琴乐音和目标提琴乐音的时变谐波能量结构映射关系；

6、s3、对高胡乐音进行音高调整与音长调整；带通滤波滤出谐波分量；应用小提琴与中提琴的时变谐波能量结构映射关系合成出中音高胡乐音，应用小提琴与大提琴的时变谐波能量结构映射关系合成出低音高胡乐音，应用小提琴与低音提琴的时变谐波能量结构映射关系合成出倍低音高胡乐音。

7、进一步地，所述步骤s1包括以下步骤：

8、s101、估计乐音的精确基频值；基频估计方法首先使用yin算法计算得到基频的粗估计值，然后通过窄带谱能量估计法估计基频的精估计值；具体步骤如下：

9、步骤s101.1：根据公式(1)计算乐音信号的差函数dt[τ]，其中，x[n]为乐音信号的时域，w为积分长度，取1024；并根据公式(2)对差函数归一化，得到归一化后的差函数dt'[τ]；

10、

11、

12、步骤s101.2：设置一个阈值，取0.05，取归一化差函数的第一个低于该阈值的极小值点作为周期点，若不存在该极值点，则取全局最小值。得到基频周期值的粗估计为n0，则基频粗估计值f0的计算由公式(3)可得，其中fs为乐音信号的采样率；

13、

14、步骤s101.3：截取乐音信号的前8192个点，对该截取信号加汉明窗，并使用快速傅里叶变换计算得到乐音信号的频域谱x[k]；

15、步骤s101.4：根据窄带谱能量的频率估计算法，乐音信号的频域谱幅度最大值的频率的估计值fes的计算由公式(4)可得，其中，kmax为频域谱最大值的索引，l为乐音信号截取长度，为8192；

16、

17、步骤s101.5：根据公式(5)计算最大幅度频率的谐波次数，其中，t代表频域谱最大值频率与基频的倍数值，根据公式(6)计算乐音信号基频的精估计值fbase，根据公式(7)计算乐音信号的周期值n；

18、

19、

20、

21、s102、对乐音信号进行单周期基频序列标记，为后续分帧提供依据；具体步骤如下：

22、步骤s102.1：取乐音信号的最大值作为搜索起始点；

23、步骤s102.2：向乐音信号右边搜索序列点。取已提取序列的最右边的点，记为nend，则在一个搜索区间内把最大的极大值点作为下一个序列点，搜索区间的左右边界le和re计算由公式(4)和公式(5)可得；

24、le＝nend+(1-ρ)×n                    公式(4)

25、re＝nend+(1+ρ)×n                    公式(5)

26、其中，ρ为搜索范围系数，取0.25，n为基频的周期数。不断通过上述方法迭代，直到搜索区间超过信号范围；

27、步骤s102.3：向乐音信号左边搜索序列点；取已提取序列的最左边的点，记为n1，则在一个搜索区间内把最大的极大值点作为上一个序列点，搜索区间的左右边界ls和rs计算由公式(6)和公式(7)可得；

28、ls＝n1-(1+ρ)×n                    公式(6)

29、rs＝n1-(1-ρ)×n                    公式(7)

30、不断通过上述方法迭代，直到搜索区间超过信号范围；最终，得到乐音信号的单周期基频序列点，表示为np＝[n1,n2,...,nm]，其中，m为乐音信号的基频周期数量；

31、s103、使用自适应频谱分辨率的短时傅里叶变换得到乐音的每一帧频率谱；具体步骤如下：

32、步骤s103.1：根据单周期基频序列点对乐音信号分帧，帧长为16个基音周期，帧移为8个基音周期，则第a帧的时域ya[m]由公式(8)表示；

33、

34、

35、其中，x[n]为乐音信号，m为乐音信号的基频周期数量，f为可以划分出的帧的数量，lx代表乐音信号的时域长度，floor表示向下取整；

36、步骤s103.2：对每一帧数据ya[m]做离散傅里叶变换，得到对应的频域谱ya[k]，最终得到频域谱序列ys＝(y1[k],y2[k],...,ya[k],...,yf[k])；

37、s104、使用自适应窗口的谐波能量结构提取方法从ya[k]中提取整数次谐波能量结构；具体步骤如下：

38、步骤s104.1：确定第b个整数次谐波的搜索区间范围，其左右边界由公式(10)和公式(11)可得；

39、

40、

41、

42、其中，lb为左边界，rb为右边界，ly为ya[k]的点数，为第b-1个整数次谐波峰在dft的位置，当b＝1时，取jb为第b次谐波搜索区间的更新步长；

43、步骤s104.2：在搜索区间[lb,rb]内找出最大的极大值点，然后记录该点作为谐波峰的位置kb，然后使用计算公式(13)该数次的谐波能量eb，其中round表示四舍五入的取整；

44、

45、

46、步骤s104.3：不断重复步骤s104.1和步骤s104.2，得到一帧时域信号的整数次谐波能量序列和整数次谐波位置其中i为最大谐波次数；

47、s105、从ya[k]中提取分数次谐波能量结构。具体步骤如下：

48、步骤s105.1：确定分数次谐波位置；第b次第c个位置的分数次谐波的位置由公式(15)计算；

49、

50、γ＝[0.25,0.5,0.75] 公式(16)

51、其中，为第b次c处位置的分数次谐波位置，为第b次整数次谐波的位置，γc表示分数次谐波的位置，分别代表第c个位置的分数次谐波在两个相邻整数次谐波间隔的位置，即在0.25、0.5、0.75处各有一个分数次谐波；

52、步骤s105.2：计算分数次谐波能量；第b次c处位置的分数次谐波的能量由公式(17)计算；

53、

54、步骤s105.3：不断重复步骤s105.1和步骤s105.2，得到一帧时域信号的整数次谐波能量序列fea和整数次谐波位置fka，其中i为最大谐波次数；

55、

56、

57、s106、计算组合乐音信号每一帧的整数次谐波能量结构和分数次谐波能量结构得到提琴乐音的时变谐波能量结构；具体步骤如下：

58、步骤s106.1：对提琴乐音在步骤s103提取的频域谱序列ys的每一帧的频域谱重复步骤s104和步骤s105，得到整数次谐波能量结构序列ies＝(ie1,ie2,...,iea,...,ief)与和分数次谐波能量结构序列fes＝(fe1,fe2,...,fea,...,fef)；

59、步骤s106.2：组合ies和fes的每一个元素，即将iea和fea组合得到ea，具体组合方式如公式(20)所示，那么，得到一个新的序列es＝(e1,e2,...,ea,...,ef)，es即是提琴乐音的时变谐波能量结构；

60、

61、s107、对小提琴midi音高为55至103的乐音样本重复步骤s101到s106提取小提琴每个乐音样本的时变谐波能量结构，同理，提取中提琴midi音高48至96的乐音样本，大提琴midi音高36至84的乐音样本和低音提琴midi音24至66的乐音样本的时变谐波能量结构。

62、进一步地，所述步骤s2包括以下步骤：

63、s201、对提取的乐音信号的时变谐波能量结构进行归一化，归一化方式为公式(21)，其中，ea(b,c)代表第a帧的第b次第c个位置的谐波能量；

64、

65、s202、线性插值对齐同一乐器同一音高的多个乐音样本，假设某个乐音样本的时变谐波能量结构es的大小为f×i×4，要对齐的帧数为ft，则目标能量结构es'的大小为ft×i×4。具体步骤如下：

66、步骤s202.1：确定插值位置，已知数据点的位置由公式(22)可得，需要插值的位置由公式(23)可得；其中，pto(i)代表第i个已知数据点的位置，ptt(j)代表第j个已知数据点的位置：

67、pto(i)＝(i-1)×(ft-1),1≤i≤f             公式(22)

68、ptt(j)＝(j-1)×(f-1),1≤j≤ft            公式(23)

69、步骤s202.2：线性插值，对于第j帧的第b次第c个位置的谐波能量，其具体计算由公式(24)可得；其中，il和ir分别表示离第j个内插点最近的左点与右点的次序；遍历每个b和c的取值，不断调用公式(24)计算内插值，即可达到对齐帧数的目的；在线性插值对齐后，令es＝es'；

70、

71、s203、：提取多个源乐器同音高乐音样本sec和多个目标乐器同音高乐音样本的能量质心tec；具体步骤如下：

72、步骤s203.1：计算某个乐音样本与其他样本的空间距离，计算方式为公式(25)；

73、

74、其中，i代表最大谐波次数，s代表乐音样本数，esi为第i个乐音样本的时变谐波能量结构，esj为第j个乐音样本的时变谐波能量结构，dai代表在第a帧该样本与其他样本的空间距离；

75、步骤s203.2：计算加权平均的权值，计算方式为公式(26)，其中，αai代表第i个乐音样本在第a帧的加权值；

76、

77、步骤s203.3：计算源乐器的能量质心sec和目标乐器的能量质心tec，计算公式分别为公式(27)和公式(28)；其中，essi代表源乐器的第i个乐音样本的时变谐波能量结构，esti代表目标乐器的第i个乐音样本的时变谐波能量结构，ss代表源乐器的乐音样本数，st代表目标乐器的乐音样本数；

78、

79、

80、s204、：计算源乐器和目标乐器的时变谐波能量结构映射关系esm，映射关系第a帧第b次第c个位置的谐波能量映射系数的计算公式为公式(29)；

81、

82、s205、：把小提琴乐音作为源乐器，中提琴、大提琴和低音提琴分别作为目标乐器，重复应用步骤s201至步骤s203，得到小提琴p音高乐音与其他提琴o的q音高的时变谐波能量结构映射关系esmpqo，p的范围取55-103，q的范围取24-96，o的范围取1-3，分别代表中提琴、大提琴和低音提琴。

83、进一步地，所述步骤s3包括以下步骤：

84、s301、对某一音高p的高胡乐音进行音高调整，将音高调整至q；音高调整通过重采样实现，重采样方式选择三次样条插值，重采样的采样率计算由公式(30)可得；

85、

86、其中，fs_new为新的采样率，fs为原采样率，fbase为音高调整前的乐音基频值，fbt为音高调整后的目标乐音基频值；经过重采样后，把其采样率设定为原采样率fs，即可得到音高调整的效果；

87、s302、对音高调整后的高胡乐音进行音长调整；通过删除基音单元来实现音长调整；具体步骤如下：

88、步骤s302.1：根据步骤s102提取的单周期基频序列点np＝[n1,n2,...,nm]，划分基音单元，则第i个基音单元xi[m]可由公式(35)，其中心点mi由公式(31)可得；

89、

90、mi＝ni 公式(32)

91、其中，m为可划分的基音单元个数，也为单周期基频序列点的个数，lx为乐音信号的时域长度，在划分基音单元后，对基音单元加汉宁窗；

92、步骤s302.2：删除基音单元；每len个基音单元要删除一个现有的基音单元，基音单元删除的间隔由公式(33)可得；

93、

94、步骤s302.3：帧还原乐音。若修改后的基音单元序列s为公式(34)，及其中心点序列sp为公式(35)；

95、

96、

97、其中，md为删除部分基音单元后的基音单元数量，那么，第i个基音单元的叠加过程可由公式(36)表示；

98、x[n+mi-1]＝x[n+mi-1]+xi[n],mi-1≤n≤mi+1 公式(36)

99、s303、带通滤波滤出高胡乐音的纯净谐波分量，首先根据谐波位置设置带通滤波器组，滤除高胡乐音整个时域的各个纯净谐波分量，然后根据步骤103.1划分每个纯净谐波分量。具体步骤如下：

100、步骤s303.1：对高胡乐音信号使用步骤s104和步骤s105的流程提取高胡乐音各个谐波的位置，得到的谐波位置由公式(37)表示。

101、

102、其中，fs为高胡乐音的采样率，lp为高胡乐音的dft的点数；

103、步骤s303.2：设置带通滤波器组，滤出第b次第c位置的谐波分量的带通滤波器的参数由公式(38)和公式(39)可得；

104、fstop(b,c)＝[fbc-0.25fbt,fbc+0.25fbt]            公式(38)

105、fpass(b,c)＝[fbc-0.05fbt,fbc+0.05fbt]            公式(39)

106、其中，fstop(b,c)为带通滤波器的阻带频率，fpass(b,c)为带通滤波器的通带频率，带通滤波器选择为数字滤波器中的fir滤波器，选择窗函数法作为fir滤波器的实现，并选择汉宁窗为窗函数类型；

107、步骤s303.3：对高胡乐音应用带通滤波器组进行滤波，得到共i×4个纯净的谐波时域分量，每个分量的时域长度与原乐音信号时域长度相同；

108、步骤s303.4：对这i×4个纯净的谐波时域分量使用步骤s103.1的方法进行分帧，共得到f×i×4个谐波分量，第a帧第b次第c个位置的纯净谐波分量可表示为p_har(a,b,c)；

109、s304、调整谐波能量。若要从音高为p的高胡乐音合成出音高为q的胡琴乐音，那么使用步骤s2提取到的esmpqo对p_har进行能量调整；具体的调整如公式(40)所示；

110、

111、s305、重叠相加法还原时域信号；叠加步骤与步骤s302.3同理，为了平滑时域波形，使不同帧的幅度有良好的过渡，使用汉宁窗对每一帧数据进行加窗处理，使其两端为零，在拼接时，重叠部分直接相加，最终得到合成的音高为q的胡琴乐音；

112、s306、对高胡midi音高为67的乐音重复步骤s301至步骤s305，其中步骤s304选择的时变谐波能量结构映射关系为esmpq1，合成出midi音高范围48至66的中音高胡乐音；对高胡midi音高为67的乐音重复步骤s301至步骤s305，其中步骤s304选择的时变谐波能量结构映射关系为esmpq2，合成出音高范围36至66的低音高胡乐音；对高胡音高midi音高为67的乐音重复步骤s301至步骤s305，其中步骤s304选择的时变谐波能量结构映射关系为esmpq3，合成出音高范围24至66的倍低音高胡乐音。

113、本发明相对于现有技术具有如下的优点及效果：

114、(1)本发明在提取乐音的精确基频时，提出了结合yin的窄带谱能量频率估计算法，该算法能够尽量避免倍频错误与半频错误，并且能够尽量减轻dft频谱分辨率带来的基频误差。

115、(2)本发明提出了自适应频谱分辨率的短时傅里叶变换提取乐音的时变谐波能量结构作为乐音的音色表征，该方法考虑的乐音的音高属性，参考基音同步叠加算法的基音标注对乐音信号进行自适应帧长的分帧，使得dft的频谱分辨率能够满足后续要求。

116、(3)本发明提出的基于时变谐波能量结构的高胡音域拓展，在参考提琴乐器的音色关系后，成功在保持胡琴音色不变的情况下合成出低音的高胡乐音。

117、(4)本发明提出的音域拓展方法基于传统的傅里叶变换分析以及基音同步叠加算法，在不需要大量数据进行模型训练下也能获得较好的音域拓展效果。